蓝桥杯AcWing 题目题解 - 数学与简单DP
目录
AcWing 1230. K倍区间 - 数学优化
AcWing 1205. 买不到的数目 - 数学公式定理
AcWing 1211. 蚂蚁感冒 - 数学思想
AcWing 2. 01背包问题 - 经典DP二维
AcWing 895. 最长上升子序列 - 经典DP一维
AcWing 1230. K倍区间 - 数学优化
枚举 O(n3)
可以很简单的写出暴力代码,直接三重循环
for(int r = 1; r <= n; r ++)
for(int l = 1; l <= r; l ++)
{
int sum = 0;
for(int i = l; i <= r; i ++)
sum += a[i];
if(sum % k == 0) ans ++;
}
枚举左右区间端点l,r,求出区间和sum判断是否为k的倍数,然后记录在答案ans上。
可以看出第三重循环的作用就是算出区间[l,r]的和,所以用前缀和来优化这重循环。
前缀和 O(n2)
预处理一下数组a[],将前缀和存入s[]中,每次查询就只需要O(1)的时间了
for(int i = 1; i <= n; i ++) s[i] = s[i - 1] + a[i]; // 求前缀和
for(int r = 1; r <= n; r ++)
for(int l = 1; l <= r; l ++)
if((s[r] - s[l - 1]) % k == 0) ans ++;
但是这个时间还是会炸,所以还需要优化一层。
数学 O(n)
第二层循环的作用是枚举左端点,写出来就是(s[r] - s[0 ~ r - 1]) % k = 0,当这个条件成立答案就加一。
化简:
s[r]%k≡s[0 ~ r−1]%k
现在这个式子的意思就是:在模k的情况下,之前所有点和当前点有多少个相等。
所以再开一个额外的数组cnt[]记录每个前缀和取余k的余数的数量,遍历一遍就行了。
代码 O(n)
#include
using namespace std;
typedef long long LL;
const int N = 100010;
int n, k;
LL s[N];
int cnt[N];
int main()
{
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; i ++)
scanf("%d", s + i), s[i] += s[i - 1]; //求前缀和
LL ans = 0;
cnt[0] = 1; //初始化
for(int i = 1; i <= n; i ++)
{
ans += cnt[s[i] % k];
cnt[s[i] % k] ++; // 前缀和取余k的余数的数量
}
cout << ans << endl;
}
这里要注意初始化cnt[0] = 1,因为上一步中l的取值范围是[0, r - 1]。(纯摘抄y总的笔记)
一个调试方法:
exit(0);作用是让程序停止,用二分法检验代码哪个位置出错
AcWing 1205. 买不到的数目 - 数学公式定理
小明开了一家糖果店。
他别出心裁:把水果糖包成4颗一包和7颗一包的两种。
糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。
当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。
大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入格式
两个正整数 n,m,表示每种包装中糖的颗数。
输出格式
一个正整数,表示最大不能买到的糖数。
数据范围
2≤n,m≤1000
保证数据一定有解。
输入样例:
4 7
输出样例:
17裴蜀定理:
若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
它的一个重要推论是:a,b互质的充分必要条件是存在整数x,y使ax+by=1.
结论:
如果a,b均是正整数且互质,那么由ax + by, x≥0,y ≥0不能凑出的最大数是(a-1)(b-1) -1。
一、打表找规律方法:
#include
using namespace std;
int n,m;
bool dfs(int x){
if(x==0)
return true;
if(x>=n&&dfs(x-n))return true;
if(x>=m&&dfs(x-m))return true;
return false;
}
int main(){
int s=0;
cin>>n>>m;
for(int i=0;i<1000;i++){
if(!dfs(i))
s=i;
}
cout< 找到规律后
#include
using namespace std;
int main()
{
int p,q;
cin >> p >>q;
cout <<(p - 1)*(q - 1)- 1 << endl;
return 0;
}
二、dp算法
#include
#include
using namespace std;
int n, m, minn, maxx, ans;
bool dp[1000000];
int main() {
cin >> n >> m;
dp[0] = true;
minn = min(n, m);
maxx = max(n, m);
if(minn>1)
ans=1;
for (int i = minn; i < n * m; i++) {
if (dp[i - minn]) {
dp[i] = true;
} else if (i >= maxx && dp[i - maxx]) {
dp[i] = true;
} else {
ans = i;
}
}
cout << ans;
return 0;
}
AcWing 1211. 蚂蚁感冒 - 数学思想
长 100 厘米的细长直杆子上有 n 只蚂蚁。
它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是 1 厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有 1 只蚂蚁感冒了。
并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
输入格式
第一行输入一个整数 n 表示蚂蚁的总数。
接着的一行是 n 个用空格分开的整数 Xi, Xi 的绝对值表示蚂蚁离开杆子左边端点的距离。
正值表示头朝右,负值表示头朝左,数据中不会出现 00值,也不会出现两只蚂蚁占用同一位置。
其中,第一个数据代表的蚂蚁感冒了。
输出格式
输出1个整数,表示最后感冒蚂蚁的数目。
数据范围
1
输入样例1:
3
5 -2 8
输出样例1:
1
输入样例2:
5
-10 8 -20 12 25
输出样例2:
3运用一个数学思想:因为蚂蚁完全相同,所以碰撞时调头等价于穿过,只是感冒+1;
第一个蚂蚁向右走的情况:
1.右边向左走的,必然被感染
2.右边向右走,必然不会被感染
3.左边向左走,必然不会被感染
4.左边向右走:
(1)右边存在向左走,则必然被感染
(2)右边不存在向左走,则必然不会被感染
#include
#include
using namespace std;
int n;
int x[51];
int main()
{
cin>>n;
for(int i=0;i>x[i];
int left=0 , right =0; //分别表示左边向右走的蚂蚁数量,和右边向左走的蚂蚁数量
for(int i=1;i0) left++;
else if(abs(x[i])>abs(x[0])&&x[i]<0) right++;
}
if(x[0]>0&&right==0||x[0]<0&&left==0) cout<<1< AcWing 2. 01背包问题 - 经典DP二维
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
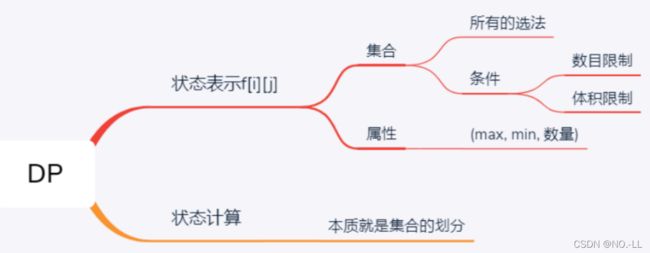
8核心套路
(1)状态f [ i ] [ j ]定义:前i个物品,背包容量j下的最优解(最大价值)∶
当前的状态依赖于之前的状态,可以理解为从初始状态 f[0][0] = 0开始决策,有N件物品,
则需要N次决策,
每一次对第 i 件物品的决策,状态 f[i][j] 不断由之前的状态更新而来。
对应代码:f[i][j]= f[i - 1][j]; 总结: 给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。 输入格式 第一行包含整数 N。 第二行包含 N 个整数,表示完整序列。 输出格式 输出一个整数,表示最大长度。 数据范围 1≤N≤1000 输入样例: 输出样例: (暴力枚举) O(n2)
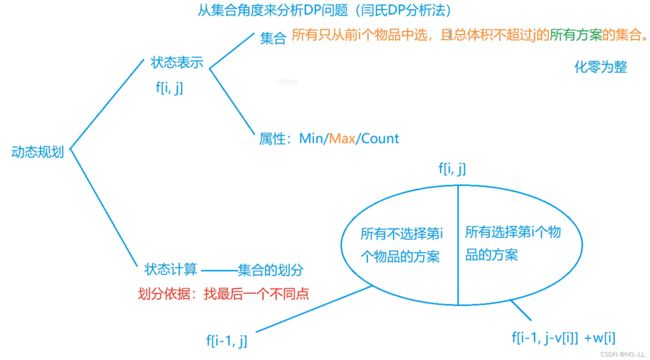
(2)当前背包容量不够(j
(3)当前背包容量够,可以选,因此需要决策选与不选第i个物品:
·选:f[i][j] = f[i - 1][j - v[i]] +w[i];
。不选: f[i][j] = f[i - 1][j];
·我们的决策是如何取到最大价值,因此以上两种情况取max()。
#includeAcWing 895. 最长上升子序列 - 经典DP一维
−109≤数列中的数≤1097
3 1 2 1 8 5 6
4
状态表示 dp[i]
集合: 所有以第i个数字结尾的上升子序列的集合
属性: 集合中的子序列长度的最大值
状态计算
枚举上升子序列的倒数第二数,不妨以坐标j表示,若 a[j] < a[i] 则 dp[i] =max(dp[i], dp[j] + 1)
备注
需要注意的是dp的长度取法不同, 对应的a[j] a[i]的坐标细节不同#include