1.线段树基础
1.1. 线段树定义
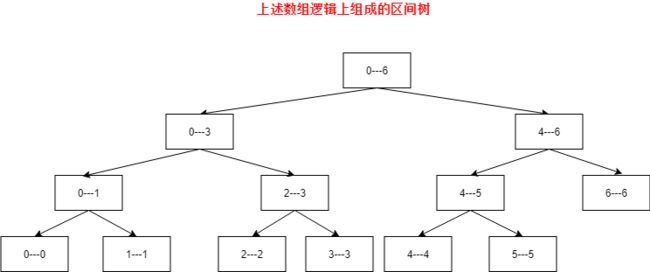
1.线段树是将一些区间进行划分,一直到最基础的单元,从根到叶子所代表的区间是包含关系
2.根节点区间代表最大的区间,所有的孩子节点都是根区间的一个子区间
3.叶子节点区间代表不可划分的粒子区间,即只代表一个元素的区间,区间左右边界相等。
1.2.构造成线段树的逻辑结构
1.3.线段树实际存储结构
采用数组来保存线段树某一段区间的值,这些区间值按照树的层序遍历的顺序保存
区间值:区间值是一个泛意,这里的区间值根据具体的需求来实现所需要的区间值的求解方式,例如,某区间的和,某区间的最大值,某区间的最小值等等
-
数组的大小:将n个元素转换成线段树,实际存储需要4n个数组空间
对于一个数量为n且具有h层的满二叉树来说,n与h具有以下关系:
1.每层数量:n = 2h-1
2.总数量:m = 2h-1
其中m与n的关系,即总h层节点数目与第h层的节点数目关系约为:m = 2n
以此推导
第一层到第h-1层节点数量 = 总节点数量 - 第h层节点数量:sum[1,h-1] = m - n = n
结论:
1.当我们知道第h层满二叉树的数目n时,就约可以求出总数约为2n
2.第h层节点数量 或 第[1,h-1]层节点数量 的2倍约等于 总节点数量
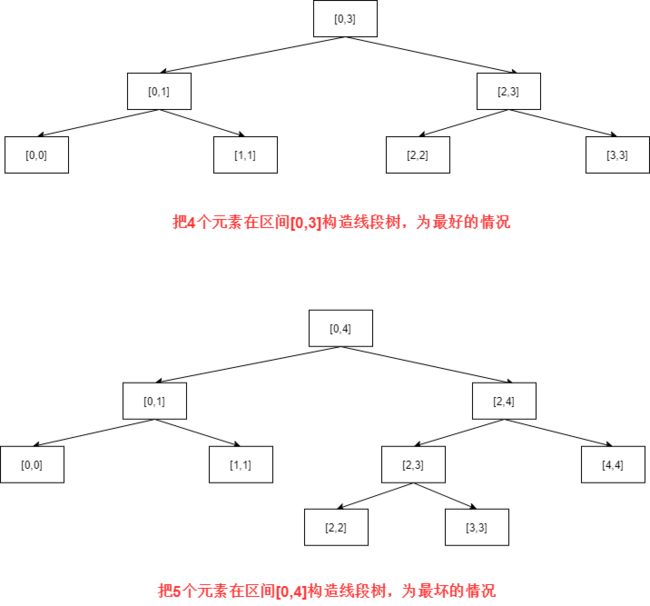
回归线段树,我们知道线段树的最小区间即每个元素的本身,在最完美的状态是所有的最小区间在同一层中,因此我们只需要2n个空间(n为构成区间树的元素)
但是最极端的情况是,有叶子节点在最后一层和倒数第二层,此时我们需要的空间大小:2n ≤ 存储空间 ≤ 4n(n为构成区间树的元素)
因此,我们取4n区间就一定可以应对最极端的情况,而平衡二叉树出现的数目一定比满二叉树的少,所以4n空间一定够用,这也出现一个问题,使用数组存储时,在树结构最完美的情况下会浪费一半左右的物理内存
区间值的存储顺序:按树的层序遍历的顺序保存,但每一个区间值并非在数组中是连续的
-
区间值的存储位置:即每个区间值的保存下标,树在层序遍历的父子关系转换成数组存储的时索引的关系。由于区间树是一种特殊的平衡二叉树,但是并不是完全二叉树,叶子节点层并非由右向左缺失,所以并不是连续的
左孩子节点 = 父节点 * 2 + 1
右孩子节点 = 父节点 * 2 + 2
父节点 = (左[右]孩子节点 - 1)/ 2
2.线段树实现
2.1. 融合器
- 区间树的值是通过定义的规则得到的,所以我们规定区间值获取接口定义,并不具体实现区间值获取的方式。而当使用区间树时,根据需求自实现这个接口定义,来满足自己要求
该接口定义为:将两个参数通过某个操作转换成一个元素返回
@FunctionalInterface
public interface Merger {
/**
* 将两个参数通过该操作转换成一个元素返回
* @param a :元素
* @param b :元素
* @return :自定义返回逻辑值
*/
E merger(E a, E b);
}
2.2. 树父子关系转换成数组索引关系
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
* @param index :该索引
* @return :左孩子节点的索引
*/
private int leftChild(int index) { return index * 2 + 1; }
/**
* 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
* @param index :该索引
* @return :右孩子节点的索引
*/
private int rightChild(int index) { return index * 2 + 2; }
2.3. 线段树构造函数
public class SegmentTree {
private E[] tree;
private E[] data;
private Merger merger;
public SegmentTree(E[] arr, Merger merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
tree = (E[]) new Object[arr.length * 4];
buildSegmentTree(0, 0, data.length - 1);
}
/**
* 在treeIndex的位置创建区间{l...r}的线段树
* @param treeIndex :tree数组中索引为treeIndex的位置 :
* tree[treeIndex] :代表tree数组中索引为treeIndex的空间中存储线段树范围为{l...r}的内容
* @param l :区间左边界
* @param r :区间右边界
*/
private void buildSegmentTree(int treeIndex, int l, int r) {
//递归到底所进行的操作(最基础的原子操作)
//当左边界等于右边界的时候,该位置存储此元素本身
if (l == r) {
tree[treeIndex] = data[l];
return;
}
//递归到底过程
//左孩子索引位置
int leftChildIndex = leftChild(treeIndex);
//右孩子索引位置
int rightChileIndex = rightChild(treeIndex);
//其孩子划分区间的中间值mid,左孩子获得的区间{l...mid},右孩子获得的区间范围{mid + 1...r}
//避免左右区间的值过大,超过整形的范围
int mid = l + (r - l) / 2;
//计算左子树区间对应的线段树
buildSegmentTree(leftChildIndex, l, mid);
//计算右子树区间对应的线段树
buildSegmentTree(rightChileIndex, mid + 1, r);
//回溯到根的过程,为每一个线段(从子线段范围到最大线段范围)区间添加进行操作的值
//存储的具体的值:和业务相关,可能存储个数,和最大值,最小值 即综合左右两个线段的信息来得到当前更大的线段的信息
tree[treeIndex] = merger.merger(tree[leftChildIndex], tree[rightChileIndex]);
}
}
1.传入一个数组,将其构造成线段树,其中data数组保存传入数组的元素,tree数组保存线段树的区间值
2.最大的区间为[0,data.length-1],以中间索引划分左右子区间,直到划分成最小的区间为数据本身;之后回溯到更大区间时,使用融合器的定义来获取该区间的值
2.4. 查询线段树某区间的值
/**
* 返回区间[queryL,queryR]的值
* @param queryL :左边界
* @param queryR :右边界
* @return :区间的值
*/
public E query(int queryL, int queryR) {
if (queryL > queryR || queryL < 0 || queryL >= data.length
|| queryR < 0 || queryR >= data.length) {
throw new IllegalArgumentException("Index is illegal.");
}
return query(0, 0, data.length - 1, queryL, queryR);
}
/**
* 在以treeIndex = 0为根的线段树的区间{l...r}的范围中,搜索区间[queryL...queryR]的值
* @param treeIndex :tree数组中索引为treeIndex的位置 :
* tree[treeIndex] :代表tree数组中索引为treeIndex的空间中存储线段树范围为{l...r}的内容
* @param l :区间树左边界
* @param r :区间树右边界
* @param queryL :查询左边界
* @param queryR :查询右边界
*/
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
//递归到底的原子操作
if (l == queryL && r == queryR) {
return tree[treeIndex];
}
//递归到底过程
//计算左孩子索引位置
int leftChildIndex = leftChild(treeIndex);
//计算右孩子索引位置
int rightChildIndex = rightChild(treeIndex);
//计算区间中点
int mid = l + (r - l) / 2;
//若查询左区间 >= mid + 1,说明查询区间,在此区间的右半子区间中
if (queryL >= mid + 1) {
return query(rightChildIndex, mid + 1, r, queryL, queryR);
}
//若查询右区间 <= mid ,说明查询区间,在此区间的左半子区间中
else if (queryR <= mid) {
return query(leftChildIndex, l, mid, queryL, queryR);
}
//查询区间在两个区间中都存在一部分
//将查询区间分成两个分别 在 此区间的右半子区间中的区间 和 在此区间的左半子区间中的区间
E leftResult = query(leftChildIndex, l, mid, queryL, mid);
E rightResult = query(rightChildIndex, mid + 1, r, mid + 1, queryR);
//计算查询区间的值:由查询子区间根据用户实现的线段树融合器实现
return merger.merger(leftResult, rightResult);
}
可以查询的区间 [L,R] 的取值范围:0 ≤ L ≤ R ≤ data.length-1
2.5. 更新构成线段树的数组的元素值,则整个线段树的涉及该值索引位置的区间及其子区间都需要更新区间值
/**
* 将index位置的值,更新成e
* @param index : 数组位置索引
* @param e :新的值
*/
public void set(int index, E e) {
//先更新数组相应位置值
data[index] = e;
//更新数组对应线段树数组有该元素的区间值
set(0, 0, data.length - 1, index, e);
}
/**
* 在以treeIndex = 0 为根的线段树中更新index的值为e
* @param treeIndex :tree数组中索引为treeIndex的位置 :
* tree[treeIndex] :代表tree数组中索引为treeIndex的空间中存储线段树范围为{l...r}的内容
* @param l :区间树左边界
* @param r :区间树右边界
* @param index :更新位置索引
* @param e :更新值
*/
private void set(int treeIndex, int l, int r, int index, E e) {
//递归到底,当左右边界相等,只有一个元素,即更新值
if (l == r) {
tree[treeIndex] = e;
return;
}
//计算该区间中间点索引,线段树左右子区间值存储位置索引
int mid = l + (r - l) / 2;
int leftChildIndex = leftChild(treeIndex);
int rightChildIndex = rightChild(treeIndex);
//当添加元素的索引 >= 该区间中间点索引,说明该点在该区间的右子区间中
if (index >= mid + 1) {
set(rightChildIndex, mid + 1, r, index, e);
} else { //说明子左子区间中
set(leftChildIndex, l, mid, index, e);
}
//当回溯时,需要从新计算修改过的线段树区间及其父区间的所有值
tree[treeIndex] = this.merger.merger(data[leftChildIndex], data[rightChildIndex]);
}
由于更新数组中某个值,相当于更新这个数组构成线段树的某个叶子节点,而与该叶子节点所有相关的父节点及祖先节点都会受到影响。
2.6.一些基础方法
public E get(int index) {
if (index < 0 | index >= data.length) {
throw new IllegalArgumentException("Index is illegal");
}
return data[index];
}
public int getSize() {
return data.length;
}
/**
* 遍历输出tree数组
*/
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("[");
for (int i = 0; i < tree.length; i++) {
if (tree[i] == null) {
res.append("NIL");
} else {
res.append(tree[i]);
}
if (i != tree.length - 1) {
res.append(",");
}
}
res.append("]");
return res.toString();
}
3.测试
- 在定义融合器的接口的时候,我添加了一个注解@FunctionalInterface,这个注解检查是否为函数式接口,这个注解作用是校验我们是否可以用lambda表达式来实现具体需求逻辑,若对此不太懂的可以查一下
- 测试的逻辑很简单,我们传入一个自定义数组的时候,同时定义融合器的具体确定区间值的方式(我这里定义区间值为区间内所有元素的和)。根据输出值直接验证即可。
public class SegmentTreeTest {
public static void main(String[] args) {
Integer[] nums = {2, -1, 3, 8, 9};
SegmentTree segmentTree = new SegmentTree<>(nums, (a, b) -> a + b);
System.out.println(segmentTree);
Integer query = segmentTree.query(1, 4);
System.out.println(query == 19);
}
}