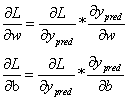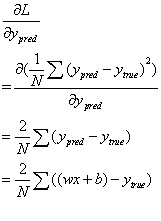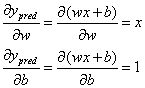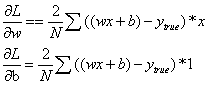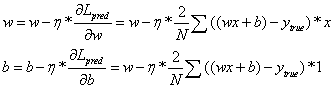1 机器学习的目标
2 获取样本数据
3 损失函数
4 减少损失函数的值
5 训练模型
机器学习的目标
从大量数据中学习到高维的抽象特征,使得新输入的x也能在经过模型后,得出一个符合实际情况的y值。
就是通过大量数据,推断出正常的公式,然后再公式中输入新的x就可以得到期望的Y
获取样本数据
若我们提前知道了某一堆样本服从下述线性模型,那么我们就有理由相信输入任意x所构成的点(x,y)都服从该线性模型分布。
y = w*x + b
但由于样本中存在不可控制的偏差(&),上述线性模型变成如下形式。导致我们需要通过大量的样本就才可以可以得到理想的w和b
y = w*x + b + &
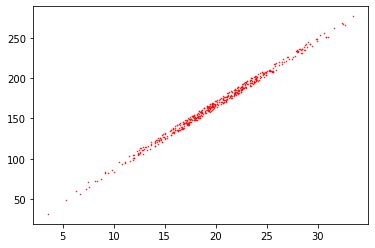
本地我们用某个 y = w*x + b生成了500个离散点数据,获取样本数据的代码如下:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
## 获取样本数据 ##
points= np.genfromtxt("../lable.csv", delimiter=",")
N = len(points)
x = []
y = []
for i in range(0, N):
x.append(points[i,0])
y.append(points[i,1])
plt.plot(x,y, "ro",color = 'red', label = "real",markersize=0.5)
plt.show()
样本数据对应的离散点图像为:
我们的目的就是通过以上样本数据,推断出 y = w*x + b的特征值w和b,是的后续有其他x值输入的时候,可以得到对应的y
损失函数
怎么才能使得推断出的y = wx+b是我们理想中的模型呢,或者是最符合原样本数据的模型呢?我们需要保证样本中的真实的y(true)值和通过模型求解出来的y(pred)值,两者之差越小越好。为了量化两者之间的差值,我们通常会使用均方误差(MSE)来进行衡量,具体公式如下:
N是样本的数量,在上面的数据集中是500;
ytrue是变量的真实值,ypred是变量的预测值
w和x就是我们要通过训练需要迭代出的样本数据特征值
顾名思义,均方误差就是所有数据方差的平均值,我们不妨就把它定义为损失函数。预测结果越好,损失就越低,训练模型就是将损失最小化。也就是在不断的迭代中,我们要通过改变初始值的w和b,使得损失函数的值越来越小,直到达到最优或者局部最优
减少损失函数的值
损失值是根据输入值,然后由权重和偏置计算出来的:
L(w,b)
损失函数中,变量只有w和b,如果要想改变L的值,那我们需要调整w或者b。如果调整一下w,损失函数是会变大还是变小?我们需要知道偏导数∂L/∂w是正是负才能回答这个问题,因为在一个曲线的增函数区间,我们需要增大w,曲线才会增大;在一个函数的减函数区间,我们需要减少w,曲线才会减小。因此,如果想要知道变量对曲线的影响是增大还是减小,需要先求出变量的导数。因此,我们需要先求出∂L/∂w和∂L/∂b的值:
根据链式求导法则:
其中:
带入以上公示后,得到线性模型分别对w和b的求导公式:
现在我们来求解下,怎么改变变量值,才能使得损失函数的值不断下降
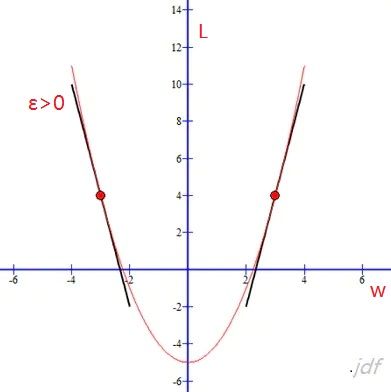
假设上图是损失函数L和w的函数图,ε表示w调整的步长(导数的意义,单位时间曲线的变化程度)
为了使得问题简单化,我们假设ε>0:
当在左方区域,也就是L成下降趋势的局域(根据偏导数的意义,我们知道(∂L/∂w<0), 我们需要减少变量w的值,是的L的值下降:
w = w + ε当在右方区域,也就是L成上升趋势的局域(∂L/∂w>0), 我们需要减少w的值,使得L的值下降:
w = w - ε
我们将步长与∂L/∂w的值关联起来
则当∂L/∂w < 0,且ε > 0时:
w < w + ε = w+(-η*∂L/∂w) = w-η*∂L/∂w,其中η为正,表示学习率
当∂L/∂w>0>时:
w < w - ε = w-(η*∂L/∂w) = w-η*∂L/∂w,其中η为正,表示学习率
当 ε<0时,推导过程是一样的;变量b的推导过程也是一样的
最终我们可以知道权重和偏置的方法:
以上公式,就是求损失函数L的最小值中用到的所谓的梯度下降法
η表示学习率,由以上推导可知,η的大小会影响权重和偏置的更新跨度,如果设置过大,可能直接就从左方的递减区域跨到了右方的递增区域
如果我们用这种方法去逐步改变模型的权重w和偏置b,损失函数会缓慢地降低,从而改进我们的模型
训练模型
训练流程如下:
- 从数据集中选择一个样本;
- 计算损失函数对对权重和偏置的偏导数;
- 使用更新公式更新每个权重和偏置;
- 回到第1步,迭代更新模型
我们用Python代码实现这个过程:
运行实例
import numpy as np
#获取样本数据
points= np.genfromtxt("lable.csv", delimiter=",")
N = len(points)
sl = 0.01;#学习率
w=0
b=0
epoch_number = 1000
for epoch in range(epoch_number):
deriv_w, deriv_b = 0., 0.
# 计算所有样本的梯度平均值
for i in range(0, N):
x = points[i,0]
y_true = points[i,1]
deriv_w += 2/N * (w * x +b - y_true)* x
deriv_b += 2/N * (w * x +b - y_true)*1
# 利用所有样本梯度的平均值更新w,b
w = w - sl * deriv_w
b = b - sl * deriv_b
# 每隔100步 计算一下当前的损失值
if epoch % 100 == 0:
current_loss = 0.
for i in range(0, N):
y_pred = w * points[i, 0] + b
y_true = points[i,1]
current_loss = current_loss + 1/N * (y_pred - y_true)**2
print('epoch :',epoch, 'current_loss:', current_loss,'w = ',w,'b = ',b)
运行结果:
epoch : 0 current_loss: 479.421982800052 w = 1.7381669767183185 b = 0.5246999270532897
epoch : 100 current_loss: 0.024288716327157032 w = 8.12668018731183 b = 2.5791541853775084
epoch : 200 current_loss: 0.014678734746904844 w = 8.09848060947496 b = 2.672836351860249
epoch : 300 current_loss: 0.008871002109283415 w = 8.076558383981164 b = 2.7456644477273477
epoch : 400 current_loss: 0.005361134987434828 w = 8.05951614423444 b = 2.802280682717526
epoch : 500 current_loss: 0.0032399686077654423 w = 8.04626758351386 b = 2.8462938897950867
epoch : 600 current_loss: 0.0019580548902253486 w = 8.035968211848195 b = 2.880509559515768
epoch : 700 current_loss: 0.0011833383027065063 w = 8.027961526522539 b = 2.9071086676510043
epoch : 800 current_loss: 0.0007151431482552472 w = 8.02173716527167 b = 2.9277866949807567
epoch : 900 current_loss: 0.0004321923167083695 w = 8.016898374760299 b = 2.9438617006567376
得到的结果为:y =8.0168x+2.94,我们的样本数据实际是由y = 8x+3然后加了一定的偏置生成的,得出的模型还是很精确的;
这是离散点和训练的模型曲线图为:
红色为真实的标签数据离散点,蓝色为训练后得出的曲线
工程目录 tensorflow