Java实现红黑树
红黑树简单介绍
红黑树是一种特殊的二叉查找树,它具有以下几点特性:
- 每个节点只有一种颜色,黑色或红色。
- 根节点是黑色。
- 叶子节点是黑色。(这里的叶子节点是指空节点)
- 如果一个节点是红色的,那么它的子节点都是黑色的。
- 从一个节点到该节点的子孙叶子节点的所有路径上包含相同数目的黑色节点
红黑树定义:
public class RedAndBlackTree> {
/**
* 红黑树节点
*/
private class TreeNode {
//父节点
private TreeNode parent;
//左孩子
private TreeNode leftChild;
//右孩子
private TreeNode rightChild;
//节点值
private E value;
//颜色
private String color;
/**
* 无参构造函数,默认初始化颜色为红色
*/
public TreeNode(){
this.color = "red";
}
/**
* 有参构造函数
* 默认初始化颜色为红色
* @param parent 父节点
* @param leftChild 左孩子
* @param rightChild 右孩子
* @param value 节点值
*/
public TreeNode(TreeNode parent,TreeNode leftChild,TreeNode rightChild,E value,String color){
this.parent = parent;
this.leftChild = leftChild;
this.rightChild = rightChild;
this.value = value;
this.color = color;
}
}
//根节点
private TreeNode root;
}
红黑树基本操作
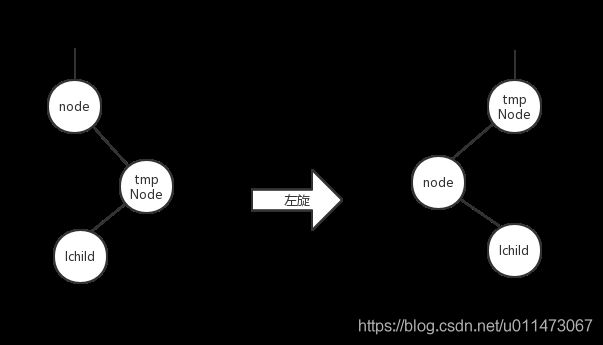
左旋
假设需要左旋的节点为node,node节点的右孩子为tmpNode,左旋步骤如下:
- 如果tmpNode为空,则无需进行任何操作。
- 记lchild为tmpNode的左孩子。
- 如果lchild不为空,将lchild设为node的右孩子,将lchild的父亲设为node,否则将node的右孩子设为空。
- 将node的父亲设为tmpNode的父亲。
- 判断如果node的父亲是空,则把tmpNode设为root节点。
- 如果node的父亲不为空,且node是它父亲的左孩子,那么将tmpNode设为node父亲的左孩子。
- 如果node的父亲不为空,且node是它父亲的右孩子,那么将tmpNode设为node父亲的右孩子。
- 将node设为tmpNode的左孩子,将node的父节点设为tmpNode。
public void leftRotate(TreeNode node){
//新建tmpNode节点,把node的右孩子赋给tmpNode
TreeNode tmpNode = node.rightChild;
if(tmpNode == null){
return;
}
TreeNode lchild = tmpNode.leftChild;
if(lchild != null){
//将tmpNode的左孩子设为node的右孩子
node.rightChild = lchild;
//将tmpNode的左孩子的父亲设为node
tmpNode.leftChild.parent = node;
}
else{
//将node的右孩子设为空
node.rightChild = null;
}
//将node的父亲设为tmpNode的父亲
tmpNode.parent = node.parent;
//判断如果node的父亲是空,则设tmpNode为root节点
if(node.parent == null){
this.root = tmpNode;
}
//如果node是它父亲的左孩子,那么将tmpNode设为node父亲的左孩子
else if(node == (node.parent.leftChild)){
node.parent.leftChild = tmpNode;
}
//否则将tmpNode设为node父亲的右孩子
else{
node.parent.rightChild = tmpNode;
}
//将node设为tmpNode的左孩子
tmpNode.leftChild = node;
//将node的父节点设为tmpNode
node.parent = tmpNode;
}
右旋
假设需要右旋的节点为node,node的左孩子为tmpNode,右旋步骤如下:
- 如果tmpNode为空,则无需进行任何操作。
- 记rchild为tmpNode的右孩子。
- 如果rchild不为空,将rchild设为node的左孩子,将rchild的父亲设为node,否则将node的左孩子设为空。
- 将node的父亲设为tmpNode的父亲。
- 判断如果node的父亲是空,则把tmpNode设为root节点。
- 如果node的父亲不为空,且node是它父亲的左孩子,那么将tmpNode设为node父亲的左孩子。
- 如果node的父亲不为空,且node是它父亲的右孩子,那么将tmpNode设为node父亲的右孩子。
- 将node设为tmpNode的右孩子,将node的父节点设为tmpNode。
public void rightRotate(TreeNode node){
//新建tmpNode节点,把node的左孩子赋给tmpNode
TreeNode tmpNode = node.leftChild;
if(tmpNode == null){
return;
}
TreeNode rchild = tmpNode.rightChild;
if(rchild != null) {
//将tmpNode的右孩子设为node的左孩子
node.leftChild = tmpNode.rightChild;
//将tmpNode右孩子的父节点设为node
tmpNode.rightChild.parent = node;
}
else{
//将node的左孩子设为空
node.leftChild = null;
}
//将node的父亲设为tmpNode的父亲
tmpNode.parent = node.parent;
//判断如果node的父亲是空,则设tmpNode为root节点
if(node.parent == null){
this.root = tmpNode;
}
//如果node是它父亲的左孩子,那么将tmpNode设为node父亲的左孩子
else if(node == (node.parent.leftChild)){
node.parent.leftChild = tmpNode;
}
//否则将tmpNode设为node父亲的右孩子
else{
node.parent.rightChild = tmpNode;
}
//将node设为tmpNode的右孩子
tmpNode.rightChild = node;
//将node的父节点设为tmpNode
node.parent = tmpNode;
}
插入新节点
一、找到插入节点的位置并插入
具体步骤如下:
- 记node为需要插入的节点(默认颜色为红色),index为需要插入的位置(初始化为root节点),parent为index的父节点(初始化为空)。
- 如果index为空,则直接将node置为根节点。
- 如果index不为空,吧index赋给parent。
- 判断node的节点值如果小于index的节点值,则将index置为index的左孩子,继续循环判断,直至index为空;如果大于index节点的值,则将index置为index的右孩子,继续循环判断,直至index为空;如果相等,证明红黑树中已存在该节点,跳出。
- 此时index为要插入的位置,parent为要插入节点的父节点,将node节点插入。
二、对插入节点进行调整
插入节点后,可能会破坏红黑树的规则,因为插入的节点是红色的,所以规则5(从一个节点到该节点的子孙叶子节点的所有路径上包含相同数目的黑色节点)不会被破坏,规则1(每个节点或者是红色,或者是黑色)、规则3(每个叶子节点是黑色,这里的叶子节点是指为空的叶子节点)显然也不会破坏,只可能破坏规则2(根节点是黑色)和规则4(如果一个节点是红的,那么它的子节点必须是黑的)。插入新节点的情况可能有以下三种:
- 插入的是根节点,此时破坏了规则2。
- 插入节点的父亲节点是黑色,此时没有破坏任何规则,无需进行调整。
- 插入节点的父亲节点是红色,此时破坏了规则4。这种情况也有5种子情况:
子情况1:父节点是红色,叔叔节点也是红色。
子情况2:父节点是红色并且是祖父节点的左孩子,叔叔节点是黑色,并且插入节点是父节点的右孩子。
子情况3:父节点是红色并且是祖父节点的左孩子,叔叔节点是黑色,并且插入节点是父节点的左孩子。
子情况4:父节点是红色并且是祖父节点的右孩子,叔叔节点是黑色,并且插入节点是父节点的左孩子。
子情况5:父节点是红色并且是祖父节点的右孩子,叔叔节点是黑色,并且插入节点是父节点的右孩子。
破坏规则后,需要对红黑树进行一系列的颜色修改以及旋转,来满足红黑树的规则,记需要调整的节点(当前节点)是node,具体步骤如下:
- 如果node节点是root节点,则将颜色变为黑色,否则进行下面的步骤。
- 如果node节点的父节点是红色并且是祖父节点的左孩子,叔叔节点也是红色,则将父节点和叔叔节点设为黑色,将祖父节点设为红色,并将祖父节点设为当前节点递归进行调整。
- 如果node节点的父节点是红色并且是祖父节点的左孩子,叔叔节点是黑色,并且node节点是父节点的右孩子,则将父节点设为当前节点并进行左旋,然后递归进行调整。
- 如果node节点的父节点是红色并且是祖父节点的左孩子,叔叔节点是黑色,并且node节点是父节点的左孩子,则将父节点设为黑色,将祖父节点设为红色并进行右旋。
- 如果node节点的父节点是红色并且是祖父节点的右孩子,叔叔节点也是红色,则将父节点和叔叔节点设为黑色,将祖父节点设为红色,并将祖父节点设为当前节点递归进行调整。
- 如果node节点的父节点是红色并且是祖父节点的右孩子,叔叔节点是黑色,并且node节点是父节点的左孩子,则将父节点设为当前节点并进行右旋,然后递归进行调整。
- 如果node节点的父节点是红色并且是祖父节点的右孩子,叔叔节点是黑色,并且node节点是父节点的右孩子,则将父节点设为黑色,将祖父节点设为红色并进行左旋。
子情况1(父节点是红色,叔叔节点也是红色)图解, 5是插入节点(当前节点),:

调整后(按步骤2和5调整)如下,20为当前节点:

对当前节点递归调整(按照步骤1调整)后满足红黑树条件:

子情况2(父节点是红色并且是祖父节点的左孩子,叔叔节点是黑色(空的叶子节点),并且插入节点是父节点的右孩子)图解,15为插入节点:

调整(按步骤3调整)后如下,此时10是当前节点:

对当前节点进行递归调整后满足红黑树条件(这种其实是子情况3,按照步骤4调整):

子情况4图解(子情况3上面已经描述,不再赘述),插入节点是25:

调整后(按照步骤6调整)如下,此时当前节点是30:
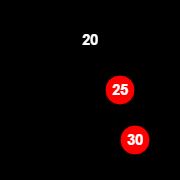
递归调整(这种其实是子情况6,按照步骤7调整)后如下,满足红黑树条件:

完整的Java代码如下:
/**
* 插入新节点
* @param value 要插入节点的值
*/
public void put(E value){
TreeNode node = new TreeNode(null,null,null,value,"red");
TreeNode index = this.root;
TreeNode parent = null;
//寻找插入位置
if(index == null){
this.root = node;
}
else{
while(index != null){
parent = index;
if(value.compareTo(index.value) < 0){
index = index.leftChild;
}
else if(value.compareTo(index.value) > 0){
index = index.rightChild;
}
else{
return;
}
}
//将node的parent设为parent
node.parent = parent;
//如果value小于parent的节点值,则将node置为parent的左孩子,否则置为右孩子
if(value.compareTo(parent.value) < 0){
parent.leftChild = node;
}
else{
parent.rightChild = node;
}
}
//进行调整
insertAdjust(node);
}
/**
* 新增节点后调整
* @param node 需要调整的节点
*/
public void insertAdjust(TreeNode node){
//如果节点为根节点,则将节点颜色变为黑色
if(this.root == node){
this.root.color = "black";
}
//如果当前节点的父节点颜色为红色
else if(node.parent != null && node.parent.color.equals("red")){
//如果父节点是左孩子
if(node.parent.parent != null && node.parent == node.parent.parent.leftChild){
//将tmpNode设为当前节点的叔叔节点
TreeNode tmpNode = node.parent.parent.rightChild;
//如果叔叔节点是红色
if(tmpNode != null && tmpNode.color.equals("red")){
//将父节点设为黑色
node.parent.color = "black";
//将叔叔节点设为黑色
tmpNode.color = "black";
//将祖父节点设为红色
tmpNode.parent.color = "red";
//将祖父节点设为当前节点
node = tmpNode.parent;
insertAdjust(node);
}
//如果叔叔节点是黑色,而且当前节点是右孩子
else if(node == node.parent.rightChild){
//将父节点设为当前节点,并进行左旋
node = node.parent;
leftRotate(node);
//接着进行调整
insertAdjust(node);
}
//如果叔叔节点是黑色,而且当前节点是左孩子
else{
//将父节点设为黑色
node.parent.color = "black";
//将祖父节点设为红色
node.parent.parent.color = "red";
//将祖父节点进行右旋
rightRotate(node.parent.parent);
}
}
else if(node.parent.parent != null){
//将tmpNode设为当前节点的叔叔节点
TreeNode tmpNode = node.parent.parent.leftChild;
//如果叔叔节点是红色
if(tmpNode != null && tmpNode.color.equals("red")){
//将父节点设为黑色
node.parent.color = "black";
//将叔叔节点设为黑色
tmpNode.color = "black";
//将祖父节点设为红色
tmpNode.parent.color = "red";
//将祖父节点设为当前节点
node = tmpNode.parent;
insertAdjust(node);
}
//如果叔叔节点是黑色,而且当前节点是左孩子
else if(node == node.parent.leftChild){
//将父节点设为当前节点,并进行右旋
node = node.parent;
rightRotate(node);
//接着进行调整
insertAdjust(node);
}
//如果叔叔节点是黑色,而且当前节点是右孩子
else{
//将父节点设为黑色
node.parent.color = "black";
//将祖父节点设为红色
node.parent.parent.color = "red";
//将祖父节点进行左旋
leftRotate(node.parent.parent);
}
}
}
}
删除节点
一、按照二叉查找树的规则将节点删除
删除节点的情况有以下三种:
情况1. 要删除的是叶子节点,此时直接删除就可以。
情况2. 要删除的节点只有一个孩子,此时用孩子顶替它即可。
情况3. 要删除的节点有两个孩子,此时需要找出它的代替节点,将代替节点的值赋给要删除的节点,然后将代替节点删除即可。代替节点为要删除节点的右子树上最小的节点,即为要删除节点的右孩子的左孩子的左孩子的左孩子…。由此可知代替节点要么只有一个右孩子,要么没有孩子,不可能有左孩子,所以对代替节点的删除可以转化为情况1和2。
假设需要删除的节点为node,代替节点为replace(replace只可能只有一个左孩子、或者只有一个右孩子、或者没有孩子),具体步骤如下:
- 如果node的左右孩子均不为空,则将replace设为node的右孩子,如果replace的左孩子不为空,循环操作将replace设为它的左孩子。
- 如果node的只有一个孩子或者没有孩子,则将replace设为node。
- 如果replace没有孩子,则判断是否为根节点,如果是根节点,则直接置空跳出;如果不是根节点并且是它父亲的左孩子,那么新建空的叶子节点tmpNode,将它父亲的左孩子设为tmpNode;如果不是根节点并且是它父亲的右孩子,那么新建空的叶子节点tmpNode,将它父亲的右孩子设为tmpNode。
- 如果replace左孩子不为空,则将tmpNode置为它的左孩子,用tmpNode代替replace,如果replace是root节点,则将tmpNode设为root节点。
- 如果replace右孩子不为空,则将tmpNode置为它的右孩子,用tmpNode代替replace,如果replace是root节点,则将tmpNode设为root节点。
- 如果replace的节点值不等于node的节点值,则将replace的节点值赋给node。
删除完后,如果replace是黑色节点时可能会破坏红黑树的规则,因此需要对tmpNode进行调整。
二、删除节点后调整
删除节点后具体有以下几种情况:
- 待调整节点是红色节点,此时将待调整节点设为黑色即可。
- 待调整节点是黑色节点并且是根节点,此时不用进行调整。
- 待调整节点是黑色节点并且不是根节点,此时需要进行调整。这种情况又分为以下几种子情况:
子情况1:待调整节点是父亲的左孩子,并且兄弟节点是红色。
子情况2:待调整节点是父亲的左孩子,并且兄弟节点是黑色,兄弟节点的两个孩子都是黑色。
子情况3:待调整节点是父亲的左孩子,并且兄弟节点是黑色,兄弟节点的左孩子是红色,右孩子是黑色。
子情况4:待调整节点是父亲的左孩子,并且兄弟节点是黑色,兄弟节点的右孩子是红色。
子情况5:待调整节点是父亲的右孩子,并且兄弟节点是红色。
子情况6:待调整节点是父亲的右孩子,并且兄弟节点是黑色,兄弟节点的两个孩子都是黑色。
子情况7:待调整节点是父亲的右孩子,并且兄弟节点是黑色,兄弟节点的右孩子是红色,左孩子是黑色。
子情况8:待调整节点是父亲的右孩子,并且兄弟节点是黑色,兄弟节点的左孩子是红色。
假设node节点是待调整节点,tmpNode节点(和第一步删除时的tmpNode不是同一节点,注意区分)是node节点的兄弟节点,具体调整步骤如下:
- 如果node节点是红色的,则将颜色变为黑色,否则继续下面步骤。
- 如果node节点是黑色的而且不是根节点,判断node节点是它父亲的左孩子还是右孩子
- 如果node是左孩子,tmpNode是红色的,则将tmpNode设为黑色,将node的父亲设为红色,将node的父亲左旋,重新将tmpNode设为node的兄弟节点继续下面步骤。
- 如果node是左孩子,tmpNode是黑色的,而且tmpNode的两个孩子(包含空叶子节点)都是黑色的,则将tmpNode设为红色,递归调整node的父节点。
- 如果node是左孩子,tmpNode是黑色的,而且tmpNode的左孩子是红色的,右孩子是黑色的,则将tmpNode的左孩子变为黑色,将tmpNode变为红色,将tmpNode右旋,重新将tmpNode设为node的兄弟节点,继续下面步骤。
- 如果node是左孩子,tmpNode是黑色的,而且tmpNode的右孩子是红色,则将node父节点的颜色赋给tmpNode,将node父节点设为黑色,将tmpNode右孩子设为黑色,将node的父亲左旋。
- 如果node是右孩子,tmpNode是红色的,则将tmpNode设为黑色,将node的父亲设为红色,将node的父亲右旋,重新将tmpNode设为node的兄弟节点继续下面步骤。
- 如果node是右孩子,tmpNode是黑色的,而且tmpNode的两个孩子都是黑色的,则将tmpNode设为红色,递归调整node的父节点。
- 如果node是右孩子,tmpNode是黑色的,而且tmpNode的右孩子是红色的,左孩子是黑色的,则将tmpNode的右孩子变为黑色,将tmpNode变为红色,将tmpNode左旋,重新将tmpNode设为node的兄弟节点,继续下面步骤。
- 如果node是右孩子,tmpNode是黑色的,而且tmpNode的左孩子是红色,则将node父节点的颜色赋给tmpNode,将node父节点设为黑色,将tmpNode左孩子设为黑色,将node的父亲右旋。
子情况1图解,已经删除的节点是20的左孩子(被空的叶子节点取代),需要调整的(当前节点)是20的左孩子(空的叶子节点):

调整(按照步骤3调整)后如下,此时当前节点的兄弟节点是25:
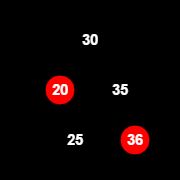
继续进行步骤3之后的步骤,此时其实是子情况2,继续调整(按照步骤4调整)后如下:

对父节点20进行递归调整后如下,满足红黑树规则:

子情况3(子情况2前面已经描述过,这里不再赘述)图解如下,已经删除的节点是20的左孩子,需要调整的节点是20的左孩子(空叶子节点):

调整(按照步骤5)后如下,此时当前节点的兄弟节点是25:

继续进行步骤5之后的步骤,这时实际上是子情况4,调整(按照步骤6)后如下,满足红黑树规则:

子情况5(子情况4前面已经描述过,这里不再赘述)图解,已经删除的节点是20的右孩子,需要调整的节点是20的右孩子(空叶子节点):

调整(按照步骤7)后如下,此时当前节点的兄弟节点是15:

继续步骤7之后的步骤,此时其实是子情况6,继续调整(按照步骤8)后如下:

递归调整父节点20后如下,满足红黑树规则:

子情况7(子情况6前面已经描述过,这里不再赘述)图解,已经删除的节点是20的右孩子,需要调整的节点是20的右孩子(空的叶子节点):

调整(按照步骤9)后如下,此时当前节点的兄弟为15:

继续步骤9之后的步骤,此时其实是子情况8,继续调整(按照步骤10)后如下,满足红黑树规则:

调整完后判断调整的节点是不是空的叶子节点,如果是则将它删除。
完整的删除代码如下:
/**
* 删除节点
* @param value 需要删除的节点值
*/
public void remove(E value){
//查找要删除的节点
TreeNode node = search(this,value);
//如果node的左孩子和右孩子都不为空,则寻找node的后继结点(右子树的最小节点),将后继结点赋给replace
TreeNode replace = null;
if(node.leftChild != null && node.rightChild != null) {
replace = node.rightChild;
while (replace.leftChild != null) {
replace = replace.leftChild;
}
}
else{
replace = node;
}
TreeNode tmpNode = null;
//如果replace为叶子节点,则直接删除
if(replace.leftChild == null && replace.rightChild == null){
//如果replace为根节点,则直接置空
if(replace == this.root){
this.root = null;
return;
}
else {
//用tmpNode空叶子节点代替replace节点,否则调整会报空指针
tmpNode = new TreeNode(replace.parent,null,null,(E)"*","black");
if (replace == replace.parent.leftChild) {
replace.parent.leftChild = tmpNode;
} else {
replace.parent.rightChild = tmpNode;
}
}
}
//如果replace左子树不为空,则用replace左子树替代replace
else if (replace.leftChild != null){
tmpNode = replace.leftChild;
if(replace == this.root){
this.root = tmpNode;
}
else if(replace == replace.parent.leftChild){
replace.parent.leftChild = tmpNode;
tmpNode.parent = replace.parent;
}
else{
replace.parent.rightChild = tmpNode;
tmpNode.parent = replace.parent;
}
}
//如果replace右子树不为空,则用replace右子树替代replace
else{
tmpNode = replace.rightChild;
if(replace == this.root){
this.root = tmpNode;
}
else if(replace == replace.parent.leftChild){
replace.parent.leftChild = tmpNode;
tmpNode.parent = replace.parent;
}
else{
replace.parent.rightChild = tmpNode;
tmpNode.parent = replace.parent;
}
}
//如果replace的值不等于node的值,则将repleace的节点值赋给node
if(replace.value.compareTo(node.value) != 0){
node.value = replace.value;
}
//如果replace为黑色节点,则对tmpNode进行删除调整
if(replace.color.equals("black")){
deleteAdjust(tmpNode);
}
//如果tmpNode是空节点,则将它删除
if(tmpNode.value.equals("*")){
if(tmpNode == tmpNode.parent.leftChild){
tmpNode.parent.leftChild = null;
}
else{
tmpNode.parent.rightChild = null;
}
}
}
/**
* 查找节点
* @param value 需要查找的节点值
* @return 节点
*/
public TreeNode search(RedAndBlackTree tree,E value){
if(tree.root == null){
return null;
}
if(value.compareTo(tree.root.value) == 0){
return tree.root;
}
else if(value.compareTo(tree.root.value) < 0){
RedAndBlackTree leftTree = new RedAndBlackTree();
leftTree.root = tree.root.leftChild;
return search(leftTree,value);
}
else{
RedAndBlackTree rightTree = new RedAndBlackTree();
rightTree.root = tree.root.rightChild;
return search(rightTree,value);
}
}
/**
* 删除节点后调整
* @param node 需要调整的节点
*/
public void deleteAdjust(TreeNode node){
//如果node是红色节点,则将node设为黑色
if(node.color.equals("red")){
node.color = "black";
}
//如果node是黑色节点,且不是根节点
else if(node != this.root){
//如果node是父亲的左孩子
if(node == node.parent.leftChild){
//将node父亲的右孩子赋给tmpNode
TreeNode tmpNode = node.parent.rightChild;
//如果node的兄弟节点tmpNode为红色
if(tmpNode.color.equals("red")){
//将node的兄弟tmpNode设为黑色
tmpNode.color = "black";
//将node的父亲设为红色
node.parent.color = "red";
//将node的父亲进行左旋
leftRotate(node.parent);
//重新将tmpNode设为node的兄弟
tmpNode = node.parent.rightChild;
}
//如果node的兄弟节点tmpNode是黑色,而且tmpNode两个孩子节点都是黑色
if(tmpNode.color.equals("black") && (tmpNode.leftChild == null || tmpNode.leftChild.color.equals("black")) && (tmpNode.rightChild == null || tmpNode.rightChild.color.equals("black"))){
//将node的兄弟节点设为红色,递归对node节点的父亲进行操作
tmpNode.color = "red";
deleteAdjust(node.parent);
}
//如果node的兄弟节点tmpNode是黑色,而且tmpNode的左孩子是红色,右孩子是黑色
if(tmpNode.color.equals("black") && tmpNode.leftChild != null && tmpNode.leftChild.color.equals("red") && (tmpNode.rightChild == null || tmpNode.rightChild.color.equals("black"))){
//将tmpNode的左孩子设为黑色
tmpNode.leftChild.color = "black";
//将tmpNode设为红色
tmpNode.color = "red";
//将tmpNode进行右旋
rightRotate(tmpNode);
//重新将tmpNode设为node的兄弟节点
tmpNode = node.parent.rightChild;
}
//如果node的兄弟节点tmpNode是黑色,而且tmpNode的右孩子是红色
if(tmpNode.color.equals("black") && tmpNode.rightChild != null && tmpNode.rightChild.color.equals("red")){
//将node父节点的颜色赋给兄弟节点tmpNode
tmpNode.color = node.parent.color;
//将node的父节点设为黑色
node.parent.color = "black";
//将tmpNode的右孩子设为黑色
tmpNode.rightChild.color = "black";
//对node的父亲进行左旋
leftRotate(node.parent);
}
}
//如果node是父亲的右孩子
else{
//将node父亲的左孩子赋给tmpNode
TreeNode tmpNode = node.parent.leftChild;
//如果node的兄弟节点tmpNode为红色
if(tmpNode.color.equals("red")){
//将node的兄弟tmpNode设为黑色
tmpNode.color = "black";
//将node的父亲设为红色
node.parent.color = "red";
//将node的父亲进行右旋
rightRotate(node.parent);
//重新将tmpNode设为node的兄弟
tmpNode = node.parent.leftChild;
}
//如果node的兄弟节点tmpNode是黑色,而且tmpNode两个孩子节点都是黑色
if(tmpNode.color.equals("black") && (tmpNode.leftChild == null || tmpNode.leftChild.color.equals("black")) && (tmpNode.rightChild == null || tmpNode.rightChild.color.equals("black"))){
//将node的兄弟节点设为红色,递归对node节点的父亲进行操作
tmpNode.color = "red";
deleteAdjust(node.parent);
}
//如果node的兄弟节点tmpNode是黑色,而且tmpNode的右孩子是红色,左孩子是黑色
if(tmpNode.color.equals("black") && tmpNode.rightChild != null && tmpNode.rightChild.color.equals("red") && (tmpNode.leftChild == null || tmpNode.leftChild.color.equals("black"))){
//将tmpNode的右孩子设为黑色
tmpNode.rightChild.color = "black";
//将tmpNode设为红色
tmpNode.color = "red";
//将tmpNode进行左旋
leftRotate(tmpNode);
//重新将tmpNode设为node的兄弟节点
tmpNode = node.parent.leftChild;
}
//如果node的兄弟节点tmpNode是黑色,而且tmpNode的左孩子是红色
if(tmpNode.color.equals("black") && tmpNode.leftChild != null && tmpNode.leftChild.color.equals("red")){
//将node父节点的颜色赋给兄弟节点tmpNode
tmpNode.color = node.parent.color;
//将node的父节点设为黑色
node.parent.color = "black";
//将tmpNode的左孩子设为黑色
tmpNode.leftChild.color = "black";
//对node的父亲进行右旋
rightRotate(node.parent);
}
}
}
}
打印红黑树
根据层次遍历思想,使用两个队列,将红黑树逐层打印(空叶子节点打印*)。
具体步骤如下:
- 将root节点入队列list1中。
- 循环操作,如果list1不为空,就出队列,将出队列的节点(记为node)入list2中,将node节点的左右孩子分别入队列list1中,如果左右孩子是空就新建一个节点值为*的树节点入队列。
- 判断list1如果不为空且其中的节点值全为*,则代表已经遍历完成,跳出循环。
- 将list1中剩余节点全部入队列list2中。
- 循环打印list2中的节点值以及颜色,每打印2的n次方个数打印一个空格(n从0开始递增)。
打印红黑树Java实现如下:
/**
* 打印红黑树,根据层次遍历思想,使用两个队列
* @param tree 需要打印的红黑树
*/
public void printTree(RedAndBlackTree tree){
TreeNode root = tree.root;
if(root == null){
return;
}
//list1队列用作层次遍历用
LinkedList list1 = new LinkedList();
//list2队列用作最后打印用
LinkedList list2 = new LinkedList();
//将根节点入队列list1
list1.addLast(root);
//如果队列list1不为空,则继续循环
while(list1.size() != 0){
//list1出队列
TreeNode node = list1.removeFirst();
//将节点存进list2队列
list2.addLast(node);
//将节点左右孩子分别入队列list1,如果为空则入节点值为*的
if(node.leftChild != null){
list1.addLast(node.leftChild);
}
else{
TreeNode tmpNode = new TreeNode(null,null,null,(E)"*","black");
list1.addLast(tmpNode);
}
if(node.rightChild != null){
list1.addLast(node.rightChild);
}
else{
TreeNode tmpNode = new TreeNode(null,null,null,(E)"*","black");
list1.addLast(tmpNode);
}
//判断如果队列list1不为空且均为*,代表遍历完成,将list1中剩余节点值均入队列list2中
boolean flag = true;
if(list1.size() == 0){
flag = false;
}
for(int num = 0;num < list1.size();num++){
if(!list1.get(num).value.equals("*")){
flag = false;
break;
}
}
if(flag == true){
while(list1.size() != 0){
TreeNode tmp = list1.removeFirst();
list2.addLast(tmp);
}
break;
}
}
//打印list2中最终结果,每打印2的n次方个数打印一个空格(n从0开始递增)
int i = 1,j = 0;
while(list2.size() != 0){
TreeNode treeNode = list2.removeFirst();
System.out.print(treeNode.value + ":" +treeNode.color + " ");
if(i == Math.pow(2,j)){
System.out.println();
i = 0;
j++;
}
i++;
}
System.out.println();
}
完整代码已经上传github:
https://github.com/3ylh3/DataStructureAndAlgorithm/tree/master/src/main/java/com/xiaobai/datastructure/redandblacktree
参考博文:https://www.cnblogs.com/skywang12345/p/3245399.html
欢迎访问我的个人博客:https://www.xiaobai.pub