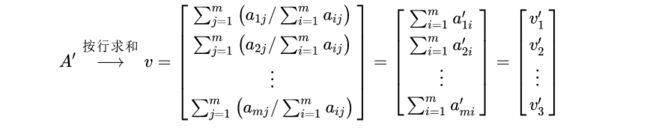【原理+代码】Python实现Topsis分析法(优劣解距离法)
目录
综合评价法
什么是Topsis法
MATLAB代码
TOPSIS法的算法步骤
数据正向化
数据标准化
考虑是否加权?(熵权法)
归一化并计算得分 (无加权)
最优最劣(加权)
TOPSIS法的评估
可视化
(AHP)层次分析法定权重
每文一语
综合评价法
评价方法一般分为两类。一类是主观赋权法,多数采取综合咨询评分确定权重,如:综合指数法、模糊综合评价法、层次分析法、功效系数法等。另一类是客观赋权法,根据各指标之间的相关关系或各指标值变异程度来确定权数,如:主成分分析法、因子分析法、理想解法等。
那么目前,主要使用的评价方法有:主成分分析法、因子分析法、TOPSIS法(本文详解)、秩和比法、灰色关联法、熵权法、层次分析法、模糊评价法、物元分析法、聚类分析法、价值工程法、神经网络法等。
是不是感觉太多了,其实当你踏进机器学习和算法,以及建模的道路当中,知识才是越学越多,越学才知道要学的东西太多了。俗话说:人外有人,天外有天,知识的海洋是无穷无尽的,学海无涯,当然要做舟呀,不然还没有入海3秒你就被淹死了,哈哈哈!
什么是Topsis法
该方法通过构造评价问题的正理想解和负理想解(各指标的最优解和最劣解),通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和负理想解的程度,来对方案进行排序,从而选出最优方案。
TOPSIS法 是根据有限个评价对象与理想化目标的接近程度进行排序的方法,是在现有的对象中进行相对优劣的评价【其中最优解的各指标值都达到各评价指标的最优值,最劣解的各指标值都达到各评价指标的最差值】
TOPSIS法 特别适合具有多组评价对象时,要求通过检测评价对象与最优解、最劣解的距离来进行排序
确定最优方案和最劣方案
计算各评价对象与最优方案、最劣方案的接近程度(典型:熵权法)
计算各评价对象与最优方案的贴近程度
这里有一个MATLAB 代码案例,可以参考使用,从熵权法到得出评分,本文还是着重从Python的角度实现。
MATLAB代码
%% 第一步:把数据复制到工作区,并将这个矩阵命名为 X
load data_water_quality.mat % 数据的名字叫 data_water_quality
%% 第二步:判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标'])
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0: ']);
if Judge == 1
Position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: ');%[2,3,4]
disp('请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ')
Type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: '); % [2,1,3]
for i = 1 : size(Position,2)
X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
end
disp('正向化后的矩阵 X = ')
disp(X)
end
%% 第三步:对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)
%% 第四步:让用户判断是否需要增加权重(可以自己决定权重,也可以用熵权法确定权重)
disp("请输入是否需要增加权重向量,需要输入1,不需要输入0")
Judge = input('请输入是否需要增加权重: ');
if Judge == 1
Judge = input('使用熵权法确定权重请输入1,否则输入0: ');
if Judge == 1
if sum(sum(Z<0)) >0 % 如果之前标准化后的Z矩阵中存在负数,则重新对X进行标准化
disp('原来标准化得到的Z矩阵中存在负数,所以需要对X重新标准化')
for i = 1:n
for j = 1:m
Z(i,j) = [X(i,j) - min(X(:,j))] / [max(X(:,j)) - min(X(:,j))];
end
end
disp('X重新进行标准化得到的标准化矩阵Z为: ')
disp(Z)
end
weight = Entropy_Method(Z);
disp('熵权法确定的权重为:')
disp(weight)
else
disp(['如果你有3个指标,你就需要输入3个权重,例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);
weight = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);
OK = 0; % 用来判断用户的输入格式是否正确
while OK == 0
if abs(sum(weight) -1)<0.000001 && size(weight,1) == 1 && size(weight,2) == m % 注意浮点数
OK =1;
else
weight = input('你输入的有误,请重新输入权重行向量: ');
end
end
end
else
weight = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同,即都为1/m
end
%% 第五步:计算与最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')
TOPSIS法的算法步骤
① 正向化(每一列都转为极大型)
② 标准化(每一个元素都被标准化处理)
③ 归一化(每一列的和都为 1 )
④ 计算权重(求每一行的和)
数据正向化
有的数据是越大越好,有的数据是靠近某个值越好,有的是在一个区间中最好,这种不同的方向和区间让分析变得混乱,为了简化分析我们将数据进行正向化处理,都让他越大越好。通常来说,常见的数据可以分为四类:
极大型指标(效益类指标):指标数值越大越好。
极小型指标(成本类指标):指标数值越小越好。
中间型指标:指标数值越接近某个值越好。
区间型指标:指标数值在某个区间范围内最好,区间中的数值大小无优劣之分。
极小型指标转化为极大型指标:(患病率)
#极小型指标 -> 极大型指标
def dataDirection_1(datas):
return np.max(datas)-datas #套公式(1)中间型指标转化为极大型指标:(ph值越接近7就越好)
#中间型指标 -> 极大型指标
def dataDirection_2(datas, x_best):
temp_datas = datas - x_best
M = np.max(abs(temp_datas))
answer_datas = 1 - abs(datas - x_best) / M #套公式
return answer_datas
区间型指标转化为极大型指标:期望指标的取值最好落在某一个确定的区间最好(如体温)
#区间型指标 -> 极大型指标
def dataDirection_3(datas, x_min, x_max):
M = max(x_min - np.min(datas), np.max(datas) - x_max)
answer_list = []
for i in datas:
if(i < x_min):
answer_list.append(1 - (x_min-i) /M) #套公式
elif( x_min <= i <= x_max):
answer_list.append(1)
else:
answer_list.append(1 - (i - x_max)/M)
return np.array(answer_list) 那么有时候,我们不是很确定最佳的区间值,可能我们在不同的专家下或者资料下,发现区间值有所波动,举一个简单的例子,假设某一个指标官方给出的是[4,5],但是就会出现一个问题,某些情况下5.5和3.5也算是不错的,如果采用后者那么就会太偏激了,采用前者又太局限了,所以我们应该如何去做呢?这里重新定义了一个公式,添加了最大容忍区间。
def dataDirection_3(datas, x_min, x_max, x_minimum, x_maximum):
def normalization(data):
if data >= x_min and data <= x_max:
return 1
elif data <= x_minimum or data >= x_maximum:
return 0
elif data > x_max and data < x_maximum:
return 1 - (data - x_max) / (x_maximum - x_max)
elif data < x_min and data > x_minimum:
return 1 - (x_min - data) / (x_min - x_minimum)
return list(map(normalization, datas))上述的转换,其实最终都是转换为正向值,不管你的方法是那种,条条大路通罗马
数据标准化
经过了正向化后,还存在一个问题就是所有的值都有它的量纲,以经过了正向化的表格数值为例,假如直接计算距离,那么肯定是肺活量越大的人越健康,比如肺活量要比其他值大得多,为了消除数据量纲的影响我们需要对数据进行标准化处理。对于每一列的数据进行标准化的方法如下:
构造加权规范矩阵,属性进行向量规范化,即每一列元素都除以当前列向量的范数(使用余弦距离度量)
# 使用sklearn里面的包,不用传统的方法
from sklearn.preprocessing import MinMaxScaler,StandardScaler,scale
def temp2(A):
max_min_scaler=StandardScaler()
A=max_min_scaler.fit_transform(A)
return A
#这种方法适合大多数类型的数据,其应用非常广泛。从公式里我们就可以看出来,转化之后其均值将变为0,而方差和标准差将变为1(考虑方差的公式),这部分如果不明白那就不妨在本子上推理一下哦。本质原理:
data = data / np.sqrt((data ** 2).sum())其他:
def Standard(datas):
K = np.power(np.sum(pow(datas,2),axis = 0),0.5)
for i in range(len(K)):
datas.iloc[: , i] = datas.iloc[: , i] / K[i]
return datas 这里可以采用自定义的标准化公式,写出原始代码,但是sklearn更加的快速的简单,正好前期更新了机器学习。
考虑是否加权?(熵权法)
熵权法是一种客观赋权方法,在具体使用过程中,根据各指标的数据的分散程度,利用信息熵计算出各指标的熵权,再根据各指标对熵权进行一定的修正,从而得到较为客观的指标权重。
如果你对某些指标,有更加的专家知识验证,那么你也可以根据算法所算出来的权重指标,自己去做一些细微的调整,可能效果更好。
#熵权法等
def entropy(df):
#返回每个样本的指数
#样本数,指标个数
n,m=np.shape(data0)
#一行一个样本,一列一个指标
#下面是归一化
maxium=np.max(data0,axis=0)
minium=np.min(data0,axis=0)
data= (data0-minium)*1.0/(maxium-minium)
##计算第j项指标,第i个样本占该指标的比重
sumzb=np.sum(data,axis=0)
data=data/sumzb
#对ln0处理
a=data*1.0
a[np.where(data==0)]=0.0001
# #计算每个指标的熵
e=(-1.0/np.log(n))*np.sum(data*np.log(a),axis=0)
# #计算权重
w=(1-e)/np.sum(1-e)
# recodes=np.sum(data*w,axis=1)
return w
plt.figure(figsize=(10,8))
sns.barplot(recodes,df.columns, orient='h')归一化并计算得分 (无加权)
def Score(sta_data):
z_max = np.amax(sta_data , axis=0)
z_min = np.amin(sta_data , axis=0)
# 计算每一个样本点与最大值的距离
tmpmaxdist = np.power(np.sum(np.power((z_max - sta_data) , 2) , axis = 1) , 0.5) # 每个样本距离Z+的距离
tmpmindist = np.power(np.sum(np.power((z_min - sta_data) , 2) , axis = 1) , 0.5) # 每个样本距离Z+的距离
score = tmpmindist / (tmpmindist + tmpmaxdist)
score = score / np.sum(score) # 归一化处理
return score最优最劣(加权)
import pandas as pd
import numpy as np
def topsis(data, weight=None):
# 归一化
data = data / np.sqrt((data ** 2).sum())
# 最优最劣方案
Z = pd.DataFrame([data.min(), data.max()], index=['负理想解', '正理想解'])
# 距离
weight = entropyWeight(data) if weight is None else np.array(weight)
Result = data.copy()
Result['正理想解'] = np.sqrt(((data - Z.loc['正理想解']) ** 2 * weight).sum(axis=1))
Result['负理想解'] = np.sqrt(((data - Z.loc['负理想解']) ** 2 * weight).sum(axis=1))
# 综合得分指数
Result['综合得分指数'] = Result['负理想解'] / (Result['负理想解'] + Result['正理想解'])
Result['排序'] = Result.rank(ascending=False)['综合得分指数']
return Result, Z, weightTOPSIS法的评估
Topsis法 的优点:
(1) 避免了数据的主观性,不需要目标函数,不用通过检验,而且能够很好的刻画多个影响指标的综合影响力度
(2) 对于数据分布及样本量、指标多少无严格限制,既适于小样本资料,也适于多评价单元、多指标的大系统,较为灵活、方便
Topsis法 的缺点:
(1) 需要的每个指标的数据,对应的量化指标选取会有一定难度
(2) 不确定指标的选取个数为多少适宜,才能够去很好刻画指标的影响力度
(3) 必须有两个以上的研究对象才可以进行使用
可视化
对不同的指标进行正向化之后,然后标准化,归一化,最终可以可视化,哈哈哈,咋感觉有一点押韵呢,那么这个这么可视化呢?
不错,就是雷达图,至于这么绘制雷达图,我这里就不做详细的讲解了,我的《炫酷可视化》专栏有,详情点击下方,即可跳转。
Python绘制雷达图之可视化神器pyecharts
先得出上述的表格,在进行可视化
合理确定指标权重是应用 TOPSIS 综合评价的关键
评价结果、评价方法的好坏,本身就具有很强的主观性。马克思主义告诉我们“具体问题具体分析。在矛盾普遍性原理的指导下,具体分析矛盾的特殊性,并找出解决矛盾的正确方法。”。怎么在论文中将你的思想、选取方法的原则、指标选取、权重构造尽可能详尽的展示,才是方法应用成功与否的关键。
做建模,切记莫要一贯定性思维,要总结前人有点,学会自主创新,才能获得真正的进步和提升
(AHP)层次分析法定权重
层次分析法是一种定性与定量相结合的决策分析方法,通过判断各衡量指标的相对重要程度,进而得到决策方案中每个指标的权重,熵权法是基于数据的定权方法,而层次分析法是基于经验的定权方法。
注意:层次分析法所提到的特征向量、特征值并不是矩阵中的概念,是重新定义的。
1) 构造指标成对比较矩阵
由于定性定权不免存在偏差,Santy 等人提出使用一致矩阵法,构造成对比较矩阵。设共有 M 个评价指标。
2) 计算矩阵的特征值和特征向量
Step 1 : 先对成对比矩阵进行列归一化,即每个元素都除以当前列元素的和
Step 2: 将归一化矩阵按行求和,得到每一行的“特征向量”
Step 3: 将特征向量按列归一化,得到“指标权重”
Step 4: 成对比矩阵的每一列乘以“指标权重”中对应位置的元素得到矩阵
3) 判断成对比较矩阵的一致性
定义: 一致性指标 CI 定义为
越趋近于0,说明一致性越好,即成对比矩阵构造合理。但多“小”依旧是人为选取,因此引入 “一致性比率” 来衡量。
定义: 一致性比率 CR,其中 CI 是一致性指标,RI 是随机一致性指标(查表得到):
本文主要介绍Python,Topsis的相关知识,至于层次分析法,后续会详细的介绍,这里只是简单提一下。
每文一语
加油!