《数据结构与算法分析：C语言描述》复习——第十章“算法设计技巧”——Minimax策略

2014.07.08 20:53

简介：

　　Minimax策略描述的是二人在轮流操作的博弈中，尽力使自己的利益最大化（Max），使对手利益最小化（Min）的一种策略。

　　这样的游戏有很多种，其中最典型的就是双人棋牌类游戏：中国象棋、五子棋、扑克牌等等。

　　这样的游戏的特点是：

　　　　1. 两人交替操作，一方先开始

　　　　2. 两人的操作互相独立，没有协作

　　游戏的种类实在太多，生活中处处是游戏。

　　“游戏”和“博弈”的英语释义都是“game”，所以我们其实可以认为理论上它们是一回事，只不过一个通俗，一个深奥。

图示：

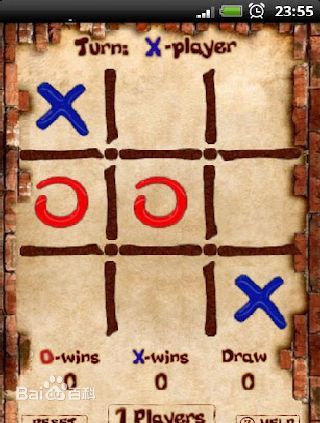
　　本次我们使用书上给出的一个非常简单的棋牌游戏“三连棋”作为例子，来解释Minimax策略。

　　如图：

　　

　　给定一个3X3的棋盘，两人轮流在上面画“O”和“X”，谁能先将三个相同符号连成一条线（横竖斜皆可），就算赢。

　　本次的代码会实现这个游戏的AI，允许你和程序来玩这个游戏。运行程序后，你会发现不论你怎么下棋，你都赢不了的。

　　因为这个游戏是公平的，没有必胜策略，因此电脑程序总能和你打成平局。

　　如果你不好好下棋，当然也会输掉。

　　

　　下面我们开始讨论Minimax策略的理论部分。

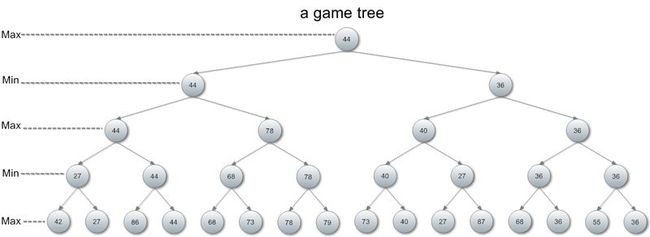
　　下面是一棵树（分叉数量我们不关心）：

　　

　　上面这棵树叫“博弈树”，英文是game tree。其中Max层和Min层交替出现。关于这棵树有四点需要解释：

　　　　1. Max层表示轮到我操作，期望我的利益最大化，所以标记为Max层

　　　　2. Min层表示轮到对手操作，期望我的利益最小化，所以标记为Min层

　　　　3. 节点中有一个数值，这个莫名其妙的数值是本章最难理解的东西——利益

　　　　4. 树的底层总是叶子节点，此处每个叶子节点都表示游戏的一种结局，因为游戏结束了，树才不会继续延伸下去

　　利益是什么？金钱，高考分数，身高体重，房子面积。总之说多了都是泪。

　　游戏中的“利益”不能用一个“赢”字来概括，否则你无法着手去分析赢的办法。

　　此处的利益，应该是具有多个参数的一个函数F(...)，函数值越大，你离“赢”就越近。

　　

　　比如下象棋，“赢”的定义是吃掉对手的“将”或者“帅”。所以你不能将“对手的将是否存在”作为利益的判断条件。

　　如果你手上现在有7个棋子，而对手只剩2个，那么很有可能你会赢，因此将双方棋子的数量差作为“利益”的标准，可能会更好。

　　同样是象棋棋子，“车”的攻击力巨大，“马”的行动灵活，“士”的防御至关重要，因此不同的棋子为你带来的潜在利益各不相同。

　　正是由于实际的游戏如此复杂，想用一个包含了很多参数的函数F(...)来表达利益才显得非常困难。

　　对于中国象棋之类的游戏，这个估值函数可以复杂到让人吐血，也可以很简单。至于用户能看到的区别，就是“电脑厉害死了”和“电脑弱爆了”。

　　

　　至此，你要随时记住一个游戏中的两个条件：

　　　　1. 赢的标准是什么（走象棋，吃掉对方的将帅）

　　　　2. 为了达到“赢”，我应该朝什么方向努力（走象棋，努力吃掉对方的棋子）

　　

　　那么三连棋呢：

　　　　1. 赢的标准，三个棋子连成一条线

　　　　2. 为了达到“赢”，你应该尽力把自己的棋子连在一起

　　

　　至此我已经不知道该怎么继续讲了，因为我思考到这儿之后就直接开始编写代码了。

　　现在你可以运行下面的代码，试试和电脑下棋，并单步调试观察运行过程。

　　如果你要自己编码实现这个程序，请记住一条原则：你如果赢了电脑，那程序就是错的。

　　在阅读代码的过程中，请尝试理解这个程序中是如何定义“利益”的。

实现：

  1 // My first attempt on Minimax , using tic-tac-toe game as a sample.
  2 #include <iostream>
  3 #include <vector>
  4 using namespace std;
  5 
  6 int function_call_count;
  7 
  8 bool computerWin(const vector<int> &board)
  9 {
 10     int i, j;
 11     
 12     for (i = 0; i < 3; ++i) {
 13         for (j = 0; j < 3; ++j) {
 14             if (board[i * 3 + j] != -1) {
 15                 break;
 16             }
 17         }
 18         if (j == 3) {
 19             return true;
 20         }
 21     }
 22     
 23     for (i = 0; i < 3; ++i) {
 24         for (j = 0; j < 3; ++j) {
 25             if (board[j * 3 + i] != -1) {
 26                 break;
 27             }
 28         }
 29         if (j == 3) {
 30             return true;
 31         }
 32     }
 33     
 34     if (board[0] == board[4] && board[4] == board[8] && board[8] == -1) {
 35         return true;
 36     }
 37     
 38     if (board[2] == board[4] && board[4] == board[6] && board[6] == -1) {
 39         return true;
 40     }
 41     
 42     return false;
 43 }
 44 
 45 bool humanWin(const vector<int> &board)
 46 {
 47     int i, j;
 48     
 49     for (i = 0; i < 3; ++i) {
 50         for (j = 0; j < 3; ++j) {
 51             if (board[i * 3 + j] != 1) {
 52                 break;
 53             }
 54         }
 55         if (j == 3) {
 56             return true;
 57         }
 58     }
 59     
 60     for (i = 0; i < 3; ++i) {
 61         for (j = 0; j < 3; ++j) {
 62             if (board[j * 3 + i] != 1) {
 63                 break;
 64             }
 65         }
 66         if (j == 3) {
 67             return true;
 68         }
 69     }
 70     
 71     if (board[0] == board[4] && board[4] == board[8] && board[8] == 1) {
 72         return true;
 73     }
 74     
 75     if (board[2] == board[4] && board[4] == board[6] && board[6] == 1) {
 76         return true;
 77     }
 78     
 79     return false;
 80 }
 81 
 82 bool fullBoard(const vector<int> &board)
 83 {
 84     for (int i = 0; i < 9; ++i) {
 85         if (board[i] == 0) {
 86             return false;
 87         }
 88     }
 89     
 90     return true;
 91 }
 92 
 93 void findComputerMove(vector<int> &board, int &best_move, int &result)
 94 {
 95     void findHumanMove(vector<int> &, int &, int &);
 96     int dc, i, response;
 97     
 98     ++function_call_count;
 99     best_move = -1;
100 
101     if (fullBoard(board)) {
102         result = 0;
103         return;
104     }
105     
106     if (computerWin(board)) {
107         result = -1;
108         return;
109     }
110     
111     for (i = 0; i < 9; ++i) {
112         if (board[i] != 0) {
113             continue;
114         }
115         board[i] = -1;
116         findHumanMove(board, dc, response);
117         board[i] = 0;
118         
119         if (best_move == -1 || response < result) {
120             result = response;
121             best_move = i;
122         }
123     }
124 }
125 
126 void findHumanMove(vector<int> &board, int &best_move, int &result)
127 {
128     void findComputerMove(vector<int> &, int &, int &);
129     int dc, i, response;
130     
131     ++function_call_count;
132     best_move = -1;
133 
134     if (fullBoard(board)) {
135         result = 0;
136         return;
137     }
138     
139     if (humanWin(board)) {
140         result = 1;
141         return;
142     }
143     
144     for (i = 0; i < 9; ++i) {
145         if (board[i] != 0) {
146             continue;
147         }
148         board[i] = 1;
149         findComputerMove(board, dc, response);
150         board[i] = 0;
151         
152         if (best_move == -1 || response > result) {
153             result = response;
154             best_move = i;
155         }
156     }
157 }
158 
159 void printBoard(const vector<int> &board)
160 {
161     cout << "  1 2 3" << endl;
162     int i, j;
163     
164     for (i = 0; i < 3; ++i) {
165         cout << i + 1;
166         for (j = 0; j < 3; ++j) {
167             cout << ' ';
168             switch(board[i * 3 + j]) {
169             case -1:
170                 cout << 'X';
171                 break;
172             case 0:
173                 cout << '.';
174                 break;
175             case 1:
176                 cout << 'O';
177                 break;
178             }
179         }
180         cout << endl;
181     }
182 }
183 
184 int main()
185 {
186     vector<int> board;
187     int n;
188     int result;
189     
190     board.resize(9, 0);
191     while (cin >> n) {
192         if (n < 0 || n >= 9 || board[n]) {
193             cout << "Invalid move" << endl;
194             continue;
195         }
196 
197         board[n] = 1;
198         printBoard(board);
199         if (humanWin(board)) {
200             cout << "You win." << endl;
201             break;
202         }
203         
204         if (fullBoard(board)) {
205             cout << "Draw." << endl;
206             break;
207         }
208         
209         result = 1;
210         function_call_count = 0;
211         findComputerMove(board, n, result);
212         cout << "Number of function calls: " << function_call_count << endl;
213         board[n] = -1;
214         printBoard(board);
215         if (computerWin(board)) {
216             cout << "Computer win." << endl;
217             break;
218         }
219         
220         if (fullBoard(board)) {
221             cout << "Draw." << endl;
222             break;
223         }
224     }
225     
226     return 0;
227 }