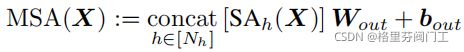精读ConViT: Improving Vision Transformerswith Soft Convolutional Inductive Biases
摘要
本文提出CNN上限太低,Vision Transformer上限高但因为需求的数据量极大而下限太低,而且训练起来更加耗时耗力。作者便希望通过结合两者的优点,达到更优秀的效果。而带有位置编码的注意力模块可以达到类似卷积的效果,因此如何将位置编码和图像结合便是本文重点。
背景知识
作者一步步地介绍了各种注意力机制,层层递进地引出了带有位置编码的注意力机制。首先介绍了单头注意力机制,这没啥好说的:
Q尺寸为L1*Dh,K尺寸为L2*Dh,Dh为图像通道数。
然后,作者开始介绍多头注意力机制。多头注意力机制可以并行地使用几个注意力头,关注不同类之间的依赖性(to allow the learning of different kinds of interdependencies)。
其中,每个注意力头的输出为![]() ,Wout尺寸为Demb*Demb,bout尺寸为Demb,为了让公式成立,Demb=Nh*Dh。而SA的计算公式又为
,Wout尺寸为Demb*Demb,bout尺寸为Demb,为了让公式成立,Demb=Nh*Dh。而SA的计算公式又为
![]()
在普通的多头注意力机制中,A即为上面第一个式子中的A。在本文中,Q和K均为L*Dh,那么A尺寸为L*L,X尺寸为L*Demb,W尺寸为Demb*Dh,那么SAh尺寸应该为L*Dh。因为Demb=Nh*Dh,那么concat后,Nh个SA变为一个L*Demb的矩阵。最后MSA为L*Demb。
但是普通的A无法探知位置信息,因此,作者又介绍了带有位置编码的注意力机制:
![]()
之间计算注意力,都是直接算出整个矩阵,而这种方法,则是一个个地计算矩阵中的每个元素。取出Q的第i行,尺寸为1*Demb,K的第j行,并转置K的第j行,尺寸为Demb*1,因此两者相乘得到一个数,其实这个数就是原来的A的第i行j列的数。但是,该注意力机制引入了一个可训练的嵌入v,长度为Dpos,Dpos>=3,和只由像素i与j的距离决定的r,这个数实际上由一个二维向量![]() 表示。
表示。
奇怪的是,这里没说这个二维向量内容是啥,或如何初始化,或如何计算,却紧接着说了这个向量怎么用。在另一篇文章中,Cordonnier等人指出,采用如下设置,带位置编码的多头注意力的输出就会类似于卷积
其中,![]() 是一个坐标,代表注意力头h最关注的像素是哪一个,
是一个坐标,代表注意力头h最关注的像素是哪一个,![]() 代表注意力头的注意力有多么集中,α越大,注意力越集中。如下图,红框代表注意力坐标,α越大,注意力图像有数值的部分越少。
代表注意力头的注意力有多么集中,α越大,注意力越集中。如下图,红框代表注意力坐标,α越大,注意力图像有数值的部分越少。
方法
上面扯了那什么多,只是为了一步步地引出最后那个通过注意力头达到卷积效果的参数设置。在作者的文章中,为了将首先使用注意力信息,然后慢慢地过渡到卷积信息,作者提出了如下模型:
FFN为前馈网络,是由GeLU激活层隔绝开的两个线性全连接层。
作者在前几层将普通的SA替换为本文提出的GPSA,而控制GPSA更像普通SA还是更像卷积的重点,就在GPSA中的那个![]() 上。
上。
![]()
![]()
GPSA中,最特别的就是A的求法。在上文提到了,当Q=K=0时,注意力头的输出才类似于卷积。而![]() 是sigmoid函数,当λ趋于无穷时,
是sigmoid函数,当λ趋于无穷时,![]() 趋于1,Q*K部分的系数就会趋于0,达到卷积的效果。但为了防止λ一直远大于1,所以每个注意力头的初始值均设为1,然后在不断的训练过程中,模型自行调整每个位置的λ,在注意力图和卷积之间做均衡和取舍。
趋于1,Q*K部分的系数就会趋于0,达到卷积的效果。但为了防止λ一直远大于1,所以每个注意力头的初始值均设为1,然后在不断的训练过程中,模型自行调整每个位置的λ,在注意力图和卷积之间做均衡和取舍。
架构细节
模型输入为224*224,分割成16*16块,每块大小14*14。每一块都得到一个长度为64的嵌入,作为不同的X。一般的模型是有12层SA,每个SA后面跟着一个FFN。而本文将前十个SA替换为了GPSA。
此外,模型学习BERT,加入了一个可学习的,名为class token的玩意,这是辅助SA捕捉位置信息的,因为GPSA包含位置编码,所以不需要这玩意。所以如上图所示,只有SA输入了class token。
实验
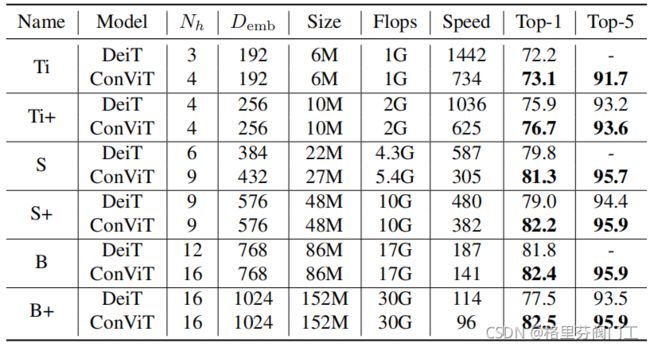
第一个实验是Nh,即每一层SA中注意力头的数量对模型性能的影响。
首先是注意力头的数目对模型性能的影响。那个Name可以看作是Model的子类,就像Resnet18和Resnet34都是Resnet的子类。Nh代表了每层SA的注意力头数目。speed表示每秒在a Nvidia Quadro GP100上能处理的图片数。
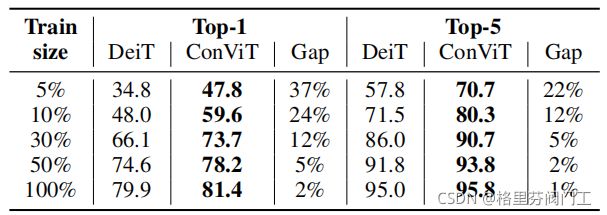
第二个实验则是实验规模对模型的的影响。
第三个实验则是着重于模型的可解释性,研究了不同训练阶段每个注意力头的σ(λ)值的变化。
这张图显示了随着训练,GPSA的关注重点的变化。这里显示了10层GPSA在训练过程中σ(λ)的变化,纵坐标即为σ(λ),黑色线条为这Nh个头的平均值。可以看到,除了第一层,前面几层中还有许多注意力头在训练后依然保留很大的σ(λ)值,说明它们倾向于卷积,更关注局部信息,而后面三层,几乎每一个注意力头的σ(λ)值都快速锐减,这说明它们更倾向于transformer结构,更关注全局的信息。
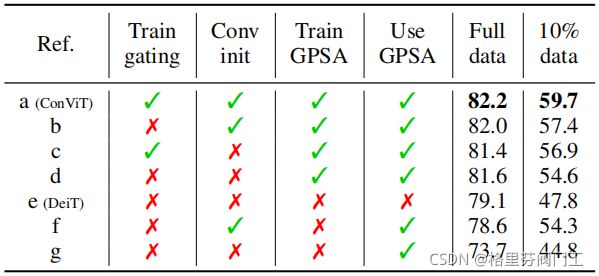
消融实验
作者探究了许多因素对模型的影响,其中大部分都好理解,而Con init是指convolutional initialization,就是根据Wq=Wk=0所在的那几个式子对GPSA中的各个值进行初始化。尽管一开始λ设置为1,理论上是综合考虑卷积和transformer的注意力的,但这样初始化,让所有GPSA层从卷积层模式开始,能小幅度提高模型性能。