数据结构之——二叉树(2)
一:二叉树的建立
1:二叉链表的结点结构定义代码
// 二叉树的二叉链表结点结构定义
typedef struct BitNode
{
TElemType data; // 结点数据
struct BitNode *lchild, *rchild // 左右孩子指针
} BitNode, *BiTree;
2:二叉树的建立的代码部分
// 按前序遍历输入二叉树中结点的值(一个字符)
// 若输入‘#’,则表示空树,构造二叉链表表示二叉树 T
void CreatBiTree(BiTree T)
{
TElemType ch;
scanf("%c", &ch);
if(ch == 'c'){
T = NULL;
}
else{
T = (BiTree)malloc(sizeof(BiTnode));
if(T == NULL){ //出现这种情况则是内存已满,无空间可分配
exit(OVERFLOW);
}
T->data = ch; //生成根节点
CreatBiTree(T->lchild); //构造左子树
CreatBiTree(T->rchild); //构造右子树
}
}
//其实树节点的建立构成是函数的递归过程。
二:线索二叉树
1:线索二叉树原理
没有引用线索二叉树原理之前:
对于一个有 n 个结点的二叉链表,每个结点都有指向左右孩子的两个指针域,所
以一共是 2n 个指针域。而 n 个结点的二叉树一共有 n-1 条分支线,所以,这种情
况下其实是存在 2n-(n-1)=n+1 个空指针域的。这些空间不存储任何事物,白白的浪
费内存的资源。
引用后:
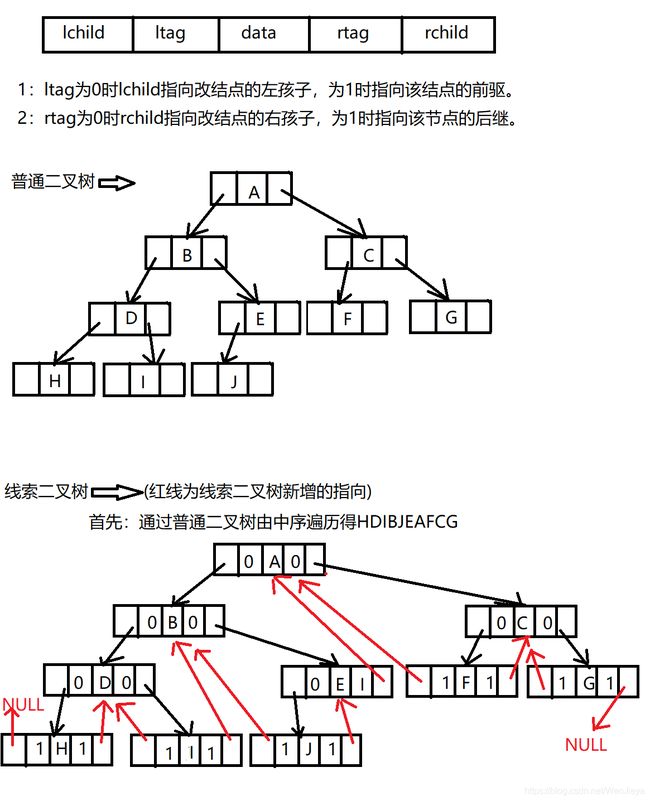
假如我们对一个二叉树进行中序遍历得到了HDIBJEAFCG这样的字符序列,遍历
过后,我们可以知道,结点 I 的前是 D ,后继是B,结点 F 的前驱是 A ,后继是
C。也就是说,我们可以很清楚的知道任意一个结点,它的前驱和后继是哪一个。我
们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应
的二叉树就称为线索二叉树。
2:线索二叉树的结点结构
typedef enum {Link, Thread} PointerTag;
// link = 0 表示指向作用孩子指针
// Thread = 0 表示指向前驱或者后继的显示
typedef struct BiThrNode
{
TElemType data; // 结点数据
struct BiThrNode *lchild, *rchild // 左右孩子指针
PointerTag LTag; //左标志
PoinTerTag RTag; //右标志
} BiThrNode, *BiThrTree;
线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱
和后继的信息只有在遍历该二叉树时才能得到,所以线索化的过程就是在遍历的过程
中修改空指针的过程。
3:中序遍历线索化的递归函数代码如下
BiThrTree pre; //定义为全局变量,始终指向刚刚访问过的结点。
//中序遍历进行中序线索化
void InThreading(BiThrTree p)
{
if(p){ //如果 p 指针不为空的话
InThreading(p->lchild); //递归左子树线索化
if(!p->lchild){ //如果没有左孩子的话
p->Ltage = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
(————————下面这行行代码后面有解析)
if(!pre->rchild){ //前驱没有右孩子
pre->RTag = Thread; //后继线索
pre->rchild = p; //前驱右孩子指针指向后继(当前结点p)
}
pre = p; //保持 pre 指向 p 的前驱
InThreading(p->rchild); //递归右子树线索化
}
}
解析:
为什么这里是 !pre->rchild 而不是向上面那样是 p->child 呢?
注意我们线索化的要求:“要得到前驱和后继的信息”
对于前驱的信息而言:很简单,就是pre,因为在进行if(!p->lchild)这个代码
之前已经执行了InThreading(p->lchild);这行代码,但是还没有执行
pre = p;这行代码,所以此时pre指针指向的结点就是当前p指针指向的结点
的前驱结点。
对于后继结点的信息而言:上面已经说了:“此时pre指针指向的结点就是当前p指
针指向的结点的前驱结点。”,所以我们还没有遍历到此时p指针指向的这个结
点的后继结点,我们只能知道此时pre指向的这个结点的后继节点是当前指针p
指向的这个结点。
前序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree p)
{
if(p){ //如果 p 指针不为空的话
if(!p->lchild){ //如果没有左孩子的话
p->Ltage = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild){ //前驱没有右孩子
pre->RTag = Thread; //后继线索
pre->rchild = p; //前驱右孩子指针指向后继(当前结点p)
}
pre = p; //保持 pre 指向 p 的前驱
InThreading(p->lchild); //递归左子树线索化
InThreading(p->rchild); //递归右子树线索化
}
}
后序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree p)
{
if(p){ //如果 p 指针不为空的话
InThreading(p->lchild); //递归左子树线索化
InThreading(p->rchild); //递归右子树线索化
if(!p->lchild){ //如果没有左孩子的话
p->Ltage = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild){ //前驱没有右孩子
pre->RTag = Thread; //后继线索
pre->rchild = p; //前驱右孩子指针指向后继(当前结点p)
}
pre = p; //保持 pre 指向 p 的前驱
}
}
4:中序遍历的代码如下
有了线索二叉树后,我们对它进行遍历时会发现,它等同于一个双向链表结构,
设置一个头节点,让其lchild指针指向二叉树的根节点,让其rchild指针指向中序
便利时访问的最后一个节点。
并且:让二叉树通过中序遍历得出的字符串中的第一个字符的节点的lchild指针
和最后一个字符的节点的rchild指针均指向头节点。这样既可以从第一个节点起顺后
继进行遍历,也可以从最后一个节点起顺前进行遍历。
/*T 指向头节点,头节点左链 lchild 指向根节点,头节点rchild指向中序遍历的
最后一个节点。
中序遍历二叉线索链表表示的二叉树*/
Status InOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p;
p = T->lchild; //p指向根节点
while(p != T){
/*我们上面说过了,让中序遍历得到的最后以一个字符其对应的节点的rchild指针
指向头节点,即T,所以当P=T时说明已经遍历到最后一个节点了,可以结束遍历了*/
while(p->LTag == 0){//当目前所在节点存在左子节点时
p = p->lchild;
}
printf("%C", p->data);//显示节点数据
while(p->Rtag == 1 && p->rchild != T){
//RTag==1说明该节点没有右子节点,rchild指向的是后继节点
//rchild != T 说明该节点的后继节点不是头节点。
p = p->rchild;
printf("%C", p->data);
}
p = p->rchild; /*执行到这一步说明该节点的RTag = 0,其存在右子
节点*/
}
}
三:树、森林与二叉树的转换
1:树转换为二叉树
规则
1:原来树的根节点仍然作为新的二叉树的根节点。
2:每个结点原来的左子树的根节点仍然作为该结点的左子树根节点。
3:每个结点同层次下右边相邻的兄弟结点作为该节点的右子树的根节点。
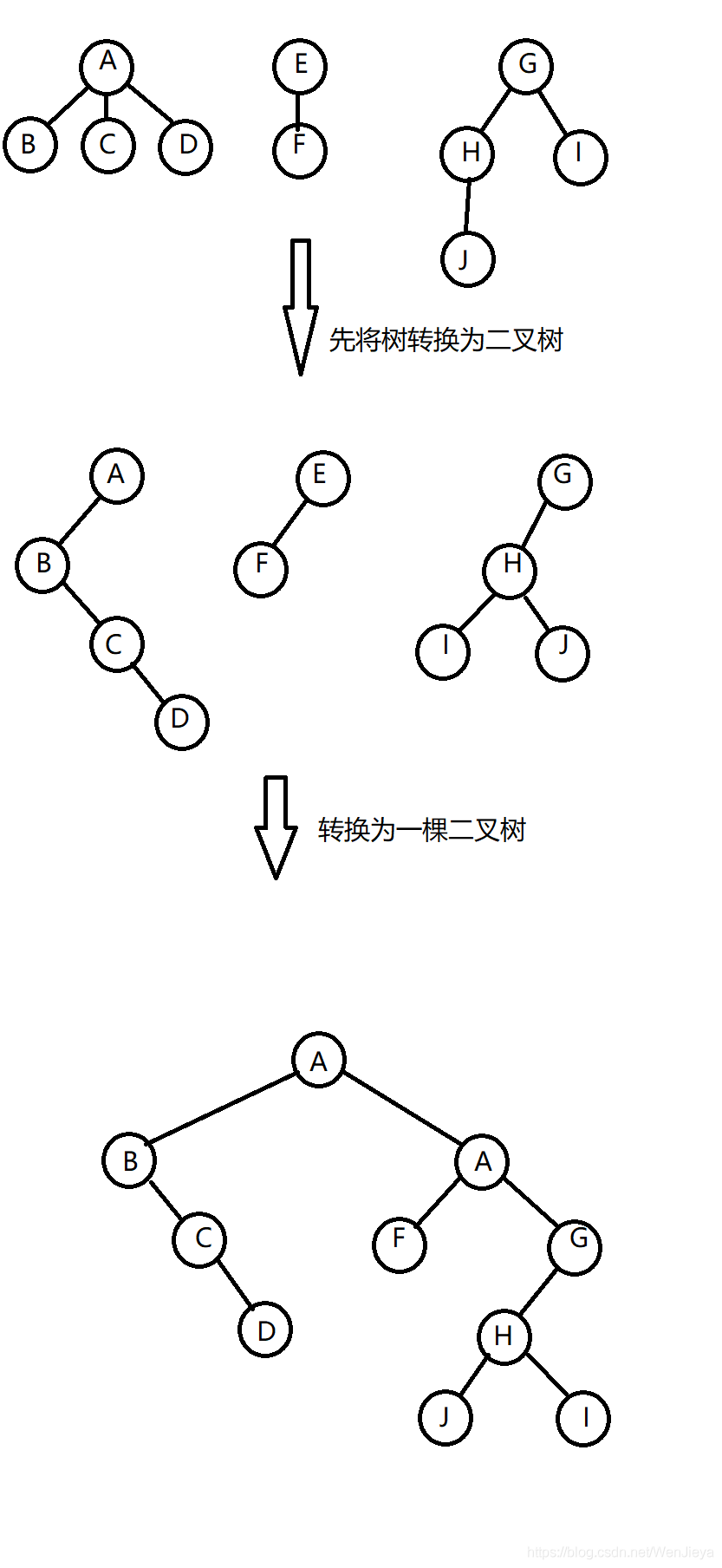
规则
1:把每个树转换为二叉树(按上面1中的方法)。
2:前一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根节点作
为前一棵的根节点的右孩子,用线连接起来。当所以的二叉树连接起来后就得到
了由森林转换而来的二叉树。
其过程就是树转换为二叉树的逆过程。
4:二叉树转换为森林
其过程就是森林转换为二叉树的逆过程(先把二叉树转化为几个二叉树,再通过3
把这几个二叉树转换为树)
四:赫夫曼树及其应用
1:初识赫夫曼编码
用电脑的人几乎都会应用压缩和解压缩软件来处理文档,因为它可以减少 文档
在磁盘上的空间,我们还可以在网络上以压缩的形式传输大量数据,使得保存和传递
都更加高效。
压缩而不出错是怎么做到的呢? 简单说:我们把要压缩的文本进行重新编码,
以减少不必要的空间。尽管现在最新技术在编码上已经很好很强大,但是这一切都
来自于曾经的技术积累,最基本的压缩编码方法——赫夫曼编码。
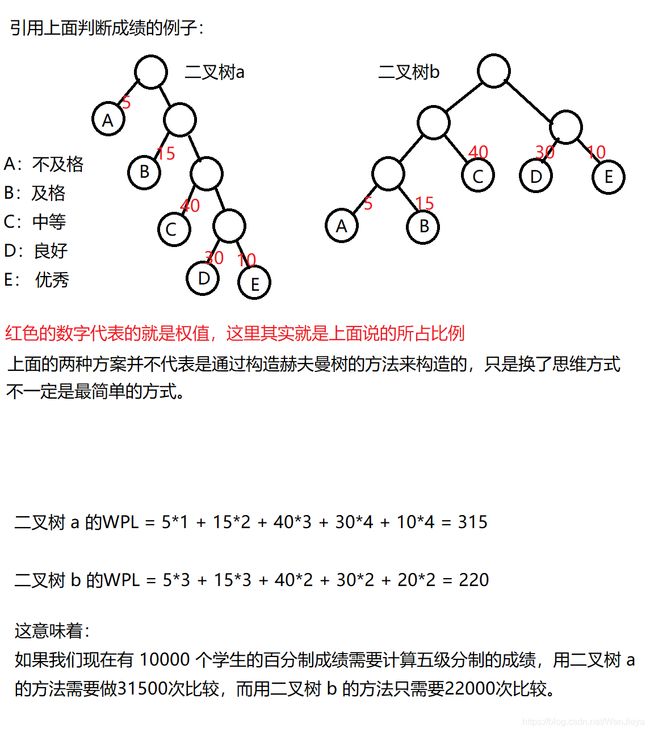
如果我们编写一个判断成绩的代码,最简单的如下:
if(a < 60){
b = "不及格";
}
else if(a < 70){
b = "及格";
}
else if(a < 80){
b = "中等";
}
else if(a < 90){
b = "良好";
}
else {
b = "优秀";
}
但是对于以上的代码,如果输入量很大的话,那效率是很有问题的,例如:70
分以上的人大约占总数的 80%,但是他们的成绩都需要经过 3 次以上的判断才能得
到结果,这显然是不合理的。
2:赫夫曼树定义与原理
【以下是特定名词】
1:路径长度:从树中一个结点到另一个结点之间的分支构成两个结点之间的路
径,路径上的分支数目称做路径长度。
3:树的路径长度:从树根到每一结点的路径长度之和。
权:树节点之间的边相关数叫做权
————————————若考虑到带权的结点
4:结点的带权路径长度:从该节点到树根之间的路径长度与结点上权的乘积。
5:树的带权路径长度:树中所有叶子结点的带权路径长度之和。
注意:带权路径长度(PWL)最小的二叉树称作赫夫曼树(也叫最优二叉树)
3:如何构造赫夫曼树
规则:
1:根据给定的 n 个权值{W1、W2.....Wn}构成 n 棵二叉树的集合 F = {T1、T2
T3........Tn},其中每棵二叉树 Ti 中只有一个带权为Wi的根节点,其左右
子树均为空。
2:在 F 中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树,且置
新的二叉树的根节点的权值为其左右子树的上根节点的权值之和。
3:在 F 中删除这两棵树,同时将新得到的二叉树加入 F 中。
4:重复 2 和 3 步骤,直到 F 只含一棵树为止。这棵树便是赫夫曼树。
假如我们有一段文字的内容为"BADCADFEED"要网络传输给别人,用二进制的数
字(0和1)来表达是很自然的。我们这段文字中有六个种类的字符:ABCDEF,其相应的
二进制数据表示为:
字母: A B C D E F
二进制字符:000 001 010 011 100 101
所以编码后的数据为:“001000011010000011101100100011”
假设六个字母的频率为A 27,B 8,C 15,D 15,E30,F 5,因此我们可以按照赫夫曼树来重新规划它们。
规则:赫夫曼树的左分支代表 0 ,右分支代表 1 ,即先根据上述,按照权值大小
构造赫夫曼树,在将赫夫曼树的左分支 改为 0 ,右分支改为 1

此时:我们对这六个字母从其根节点到叶子节点所经过路径的 0 或 1来编码,可以得到以下定义:
字母: A B C D E F
二进制字符: 01 1001 101 00 11 1000
所以:
原编码二进制串:001000011010000011101100100011(30个字符)
新编码二进制串:10010100101010010000111100(25个字符)
随着字符的增加和多字符权重的不同,这种压缩会更加显示出它的优势。
注意:
1:若要设计长短不等的编码,则必须是任一字符的编码都不是另一个字
符的码的前缀(因为非常容易混淆),这种编码称作前缀编码。
2:在解码时,还是要用到赫夫曼树的,所以发送方和接收方必须要约定好同样
的赫夫曼编码规则。