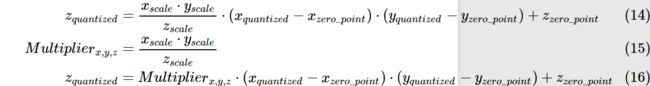模型量化原理及tflite示例
什么是量化
模型的weights数据一般是float32的,量化即将他们转换为int8的。当然其实量化有很多种,主流是int8/fp16量化,其他的还有比如
- 二进制神经网络:在运行时具有二进制权重和激活的神经网络,以及在训练时计算参数的梯度。
- 三元权重网络:权重约束为+1,0和-1的神经网络
- XNOR网络:过滤器和卷积层的输入是二进制的。 XNOR 网络主要使用二进制运算来近似卷积。现在很多框架或者工具比如nvidia的TensorRT,xilinx的DNNDK,TensorFlow,PyTorch,MxNet 等等都有量化的功能.
量化的优缺点
量化的优点很明显了,int8占用内存更少,运算更快,量化后的模型可以更好地跑在低功耗嵌入式设备上。以应用到手机端,自动驾驶等等。缺点自然也很明显,量化后的模型损失了精度。造成模型准确率下降.
量化的原理
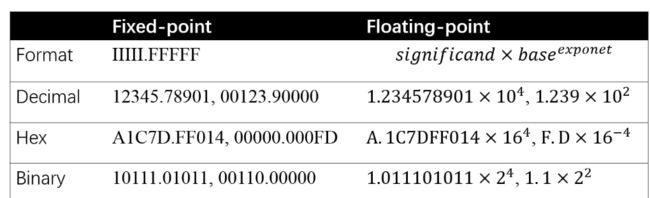
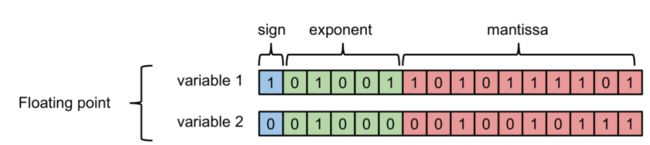
先来看一下计算机如何存储浮点数与定点数:
其中负指数决定了浮点数所能表达的绝对值最小的非零数;而正指数决定了浮点数所能表达的绝对值最大的数,也即决定了浮点数的取值范围。float的范围为-2^128 ~ +2^128. 可以看到float的值域分布是极其广的。
说回量化的本质是:找到一个映射关系,使得float32与int8能够一一对应。那问题来了,float32能够表达值域是非常广的,而int8只能表达[0,255].
怎么能够用255个数代表无限多(其实也不是无限多,很多,但是也还是有限个)的浮点数?
幸运地是,实践证明,神经网络的weights往往是集中在一个非常狭窄的范围,如下:
所以这个问题解决了,即我们并不需要对值域-2^128 ~ +2^128的所有值都做映射。但即便是一个很小的范围,比如[-1,1]能够表达的浮点数也是非常多的,所以势必会有多个浮点数被映射成同一个int8整数.从而造成精度的丢失.
这时候,第二个问题来了,为什么量化是有效的,为什么weights变为int8后,并不会让模型的精度下降太多?在搜索了大量的资料以后,我发现目前并没有一个很严谨的理论解释这个事情.
您可能会问为什么量化是有效的(具有足够好的预测准确度),尤其是将 FP32 转换为 INT8 时已经丢失了信息?严格来说,目前尚未出现相关的严谨的理论。一个直觉解释是,神经网络被过度参数化,进而包含足够的冗余信息,裁剪这些冗余信息不会导致明显的准确度下降。相关证据是,对于给定的量化方法,FP32 网络和 INT8 网络之间的准确度差距对于大型网络来说较小,因为大型网络过度参数化的程度更高
和深度学习模型一样,很多时候,我们无法解释为什么有的参数就是能work,量化也是一样,实践证明,量化损失的精度不会太多,do not know why it works,it just works.
如何做量化
由以下公式完成float和int8之间的相互映射.
![]()
其中参数由以下公式确定:
举个例子,假设原始fp32模型的weights分布在[-1.0,1.0],要映射到[0,255],则![]() ,
,![]()
量化后的乘法和加法:
依旧以上述例子为例:
我们可以得到0.0:127,1.0:255的映射关系.
那么原先的0.0 X 1.0 = 0.0 注意:并非用127x255再用公式转回为float,这样算得到的float=(2/255)x(127x255-127)=253
我们假设所有layer的数据分布都是一致的.则根据上述公式可得zquantized=127zquantized=127,再将其转换回float32,即0.0.
同理加法:
参考原文:
模型量化原理及tflite示例 - core! - 博客园模型量化 什么是量化 模型的weights数据一般是float32的,量化即将他们转换为int8的。当然其实量化有很多种,主流是int8/fp16量化,其他的还有比如 二进制神经网络:在运行时具有二进https://www.cnblogs.com/sdu20112013/p/11960552.html