【opencv-python】全景图像拼接
参考资料
- Panoramic Image Mosaic
- R. Szeliski and H.-Y. Shum. Creating full view panoramic image mosaics and texture-mapped models, SIGGRAPH 1997, pp251-258.
- M. Brown, D. G. Lowe, Recognising Panoramas, ICCV 2003.
概述
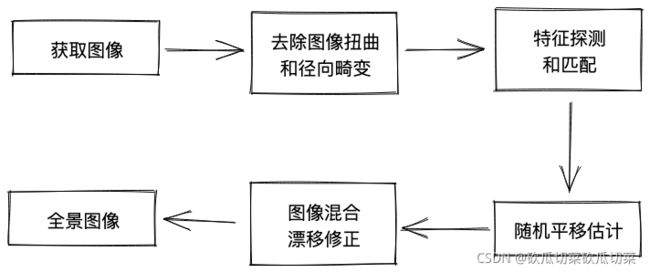
图像全景拼接技术对于商用和艺术领域都有很高的价值。自从摄影术诞生以来,人们发明了许多特定的设备来制作全景图像,但由于价格低廉的数码相机也可以胜任,使得人们对自动全景图像拼合的需求度大大增加。在我们这个示例项目中,我们使用圆柱形扭曲创建全景图像。圆柱形翘曲是最容易实现的,但它有严格的要求,所有的图像必须采取相机放置或已知的倾斜角度。而使用这种方法,我们不需要进行完全单应性计算,只需要沿角度方向进行平移即可创建全景图像。技术路线图如下图所示:
 正向翘曲:
正向翘曲:
根据图像坐标 ( x , y ) (x,y) (x,y),获得柱面投影坐标 ( x ′ , y ′ ) (x',y') (x′,y′)可以按照下式计算:
x ′ = s ⋅ θ = s ⋅ t a n − 1 ( x / f ) y ′ = s ⋅ h = s ⋅ y x 2 + f 2 x'=s·θ=s·tan^{-1}(x/f)\\ y'=s·h=s·\frac{y}{\sqrt{x^2+f^2}} x′=s⋅θ=s⋅tan−1(x/f)y′=s⋅h=s⋅x2+f2y
反向翘曲:
从柱面投影坐标 ( x ′ , y ′ ) (x',y') (x′,y′)计算图像坐标 ( x , y ) (x,y) (x,y)可以按照下式计算:
x = f ⋅ t a n θ = s ⋅ t a n − 1 ( x ′ / s ) y = h ⋅ ( x 2 + f 2 ) = y ′ / s ⋅ f ⋅ 1 + t a n 2 ( x ′ / s ) = f ( y ′ s ) ⋅ s e c ( x ′ s ) x=f·tanθ=s·tan^{-1}(x'/s)\\ y=h·\sqrt(x^2+f^2)=y'/s·f·\sqrt{1+tan^2(x'/s)}=f(\frac{y'}{s})·sec(\frac{x'}{s}) x=f⋅tanθ=s⋅tan−1(x′/s)y=h⋅(x2+f2)=y′/s⋅f⋅1+tan2(x′/s)=f(sy′)⋅sec(sx′)
在前向翘曲中,源图像映射到柱面上,但它可以在目标图像中产生空洞(因为某些像素可能永远不会映射到那里)。因此,我们使用反向映射,将目标图像中的每个像素映射到源图像。由于这两种映射都不可能精确到像素值,因此使用双线性插值来计算目标像素处的颜色。
径向畸变
由于相机中经常使用厚镜头,因此有必要校正图像中的径向畸变。一种常用的简化畸变模型如下式表达:
x d = x u ( 1 + k 1 ∗ r 2 + k 2 ∗ r 4 ) y d = y u ( 1 + k 1 ∗ r 2 + k 2 ∗ r 4 ) x_d=x_u(1+k_1*r^2+k_2*r^4)\\ y_d=y_u(1+k_1*r^2+k2*r^4) xd=xu(1+k1∗r2+k2∗r4)yd=yu(1+k1∗r2+k2∗r4)
其中 ( x d , y d ) (x_d,y_d) (xd,yd)是失真图像像素的位置, ( x u , y u ) (x_u,y_u) (xu,yu)是失真修正后(非失真)的图像位置。 ( k 1 , k 2 ) (k_1,k_2) (k1,k2)取决于相机本身,并且可以通过相机标定技术获取。反向映射和镜像畸变矫正都需要插值技术进而计算目标图像像素的颜色值。插值技术比较容易实现,可以实现对特征的平滑,因此这步要得到高质量的最终目标图像。在应用中有两个地方需要进行插值,一是反向翘曲阶段从柱面图像变换到源图像;二是从非失真图像灰度变换到失真图像灰度。我们可以把上述两步骤和计算柱面图像灰度值直接结合起来,进而避免中间的插值过程。源图像如下图所示:

畸变图像如下图所示:
SIFT特征检测
我们直接使用SIFT特征检测算法去在每张图片里面生成特征,每个SIFT描述子是128个字符长度,这些特征与相邻图像进行匹配以估计平移量。由于可能出现一定数量可能使最终图像错位的离群点,我们使用RANSAC算法去消除最终估计里产生的离群点,如下图所示:

随机抽样一致性平移变换(Ransac Translation)
随机抽样一致性(RANSAC:Random sample consensus)算法是一种可用于计算现存异常值中完全单应性的通用算法。柱面翘曲方法的使用具备只需要计算翘曲图像中平移运动的优势。同样适用于平移估计,只需一个特征就足够了。RANSAC估计方法给予容差值去计算非离群点数量,容差值基于图像噪声确定。由于我们的图像获取质量较高,为取得较好的估计效果,两个像素的容差值就足够了(我们发现图像中只有5-10%数量的离群点)。
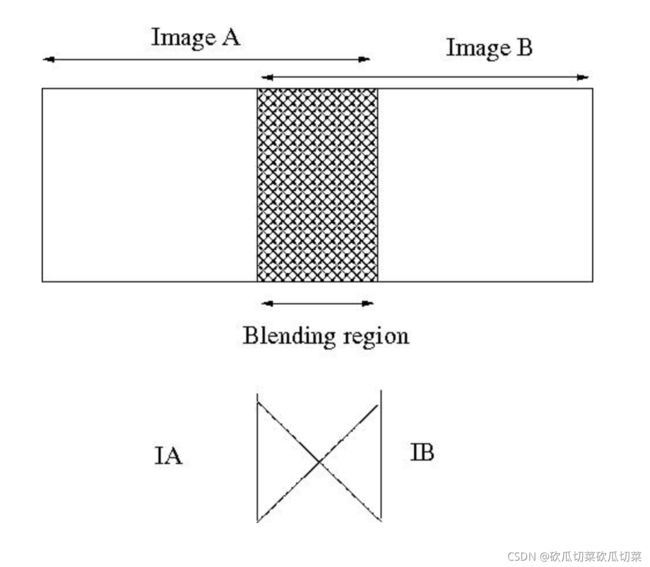
图像融合
在这个最简单的方法中,融合区域中的像素值通过两个交叠图像加权平均的方式确定。有时这个简单的方法不起作用(例如在一些曝光差异存在的场景中)。但是在我们的场景中,所有的图像都是保证相机架在三脚架上同时拍摄,因此这个简单的算法可以获得完美的结果。加权平均图像融合算法的数学表达为:
P B ( i , j ) = ( 1 − w ) ⋅ P A ( i , j ) + w ⋅ P B ( i , j ) PB(i,j)=(1-w)·PA(i,j)+w·PB(i,j) PB(i,j)=(1−w)⋅PA(i,j)+w⋅PB(i,j)
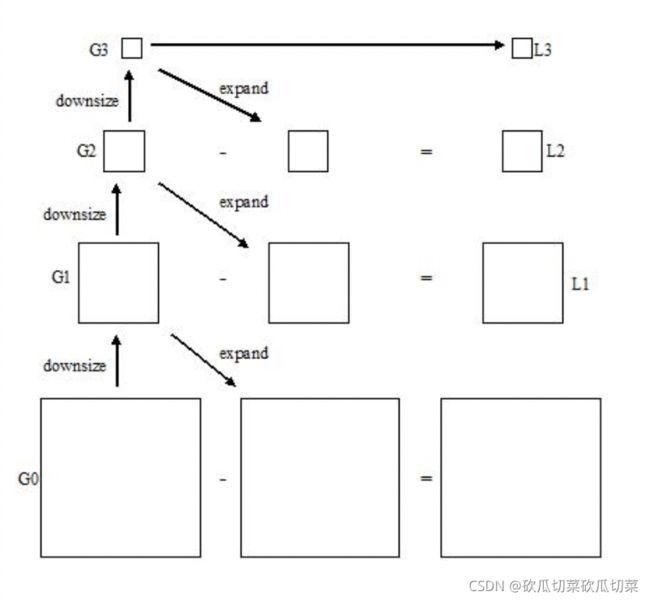
金字塔融合
拉普拉斯金字塔是一种使用高斯核在融合图像时能同时保持足够多特征的算法。这种算法通过高斯核将图像降维至不同的等级(尺寸)。随后将高斯核扩展到较低的级别,并从该级别的图像中提取以获得拉普拉斯图像,原理如下图所示:
在为了交叠图像A和B生成完拉普拉斯金字塔之后,我们将两个图像在不同拉普拉斯等级通过彼此部分图像融合起来,如下图所示:
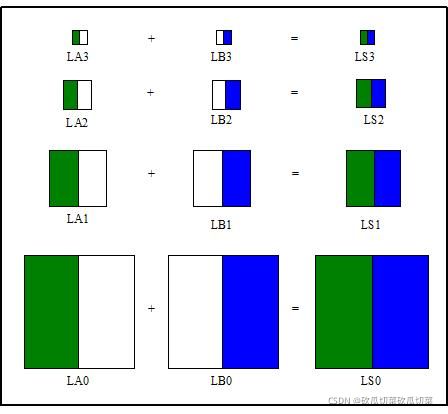
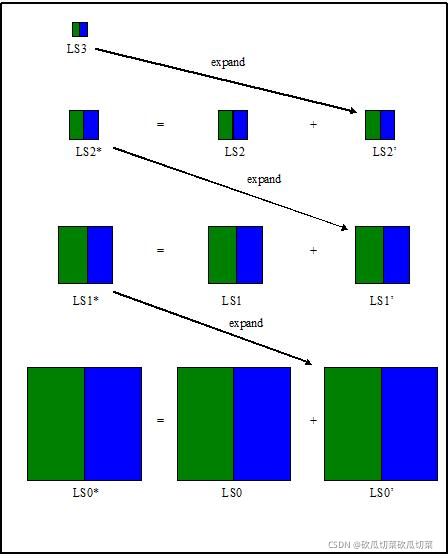
然后,我们将LS从顶级向下一级(N-1)扩展并将其添加到在相关层中的原始拉普拉斯图像中,进而生成相关层中的最新的拉普拉斯图像。我们重复这个过程直至最低级,最终得到融合图像结果,image A apple如下图所示:

image B orange如下图所示:

特征融合结果:

拉普拉斯金字塔融合结果:

漂移修正:
视场内第一张图片和最后一张图片经常没有很对齐,这种对不齐可以通过“剪切翘曲”和其他光束评查算法调整。在我们的案例中,由于不对齐的量值仅仅是1-2像素,所以我们无需做调整。
结果:
我们使用Canon SX100相机和Kedan三脚架做实验,一些相机的具体信息如下所示:
- 相机分辨率:480✖️640;
- 相机焦距:678.0541;
- k1:-0.22982
- k2:0.22952
下面是我们实现的两张全景图拼接效果:
感谢支持,欢迎关注,丰富技术/学术内容持续更新!
opencv-python快速入门视频教程
