基于Python的深度学习理论与实现（P8——误差反向传播算法）

误差反向传播算法

 之前，我们使用数值微分计算了神经网络的权重参数的梯度（严格来说，是损失函数关于权重参数的梯度）。数值微分容易实现，但是缺点在于计算上比较耗费时间。所以，在训练神经网络时，一般使用误差反向传播 算法来高效的计算权重参数的梯度。

计算图

 书中以计算图的方法引入关于反向传播算法的概念。
 计算图将计算过程用图形的方式表现出来，这里的图指的是数据结构图，即节点和边。现在我们用计算图来表示计算过程：

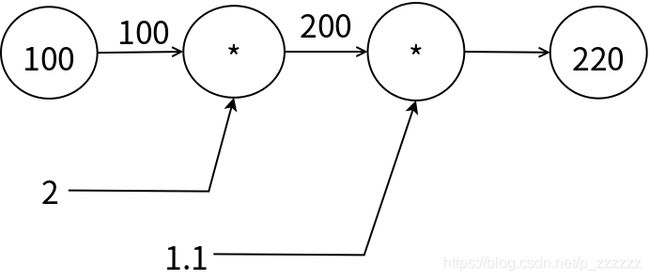
 图示中为一个简单的计算图示例，其中输入为100，输出为220，输入到输出称为计算图的正向传播，它先后经过了两个乘节点，第一个乘节点参数为2，第二个乘节点参数为1.1；当然我们也可以将参数放到节点中，或者用不同的形状来表示计算节点。
 通过上例可以看出计算图就是一个用图来描述计算过程的方法，我们再看一个更为复杂的计算图，这次我们用方形节点表示输入输出，圆形节点表示计算：

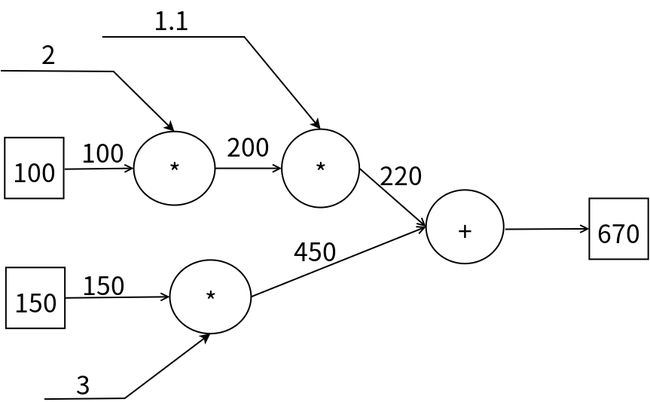
 这个示例中加入了新增的节点类型——加法。计算图的独特之处在于可以通过传递局部计算获得最终结果，局部计算指的是无论全局发生了什么，都只需要根据与自己相关联的信息计算结果即可，比如下图：

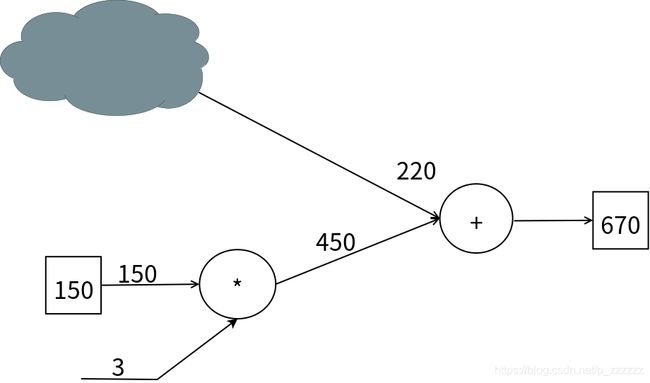
 图中，我们将原本的左上部分的输入以及节点用云来表示，对于加法节点而言，完全无需知道云中的内容即可执行计算。计算图可以集中精力于局部计算，无论全局的计算有多么复杂，各个步骤所要做的就是对象节点的局部计算。虽然局部计算非常简单，但是通过传递它的计算结果可以获得全局的复杂计算结果。
 计算图除了局部计算的优势以外，另外一大优势在于可以通过反向传播高校的计算导数。

利用计算图的反向传播

 计算图的局部计算的优势在反向传播中也有显现。计算图的正向传播是将信号经过函数映射得到输出，而计算图的反向传播也是将信号经过函数映射得到输出，二者的本质是相同的，只是反向相反，更为重要的是，反向传播的函数映射是特殊的：将输入信号乘以当前节点的局部导数。

 图中，输入信号x正向传播通过f节点得到Y，用数学表达为：
$$y=f(x)$$
 在反向传播过程中，输入信号E通过反向传播，得到E’，E’是输入信号乘以局部导数，用数学表达为：
$$E^{\prime }=E\times \frac{\partial y}{\partial x}$$
 假设我们的节点为平方计算，即正向传播为：
$$y=f(x)=x^2$$
 同时假设反向传播的信号值为a，则：
$$E^{\prime }=a\times 2\times x$$
 下面我们来看反向传播更复杂一些的例子，如下图：

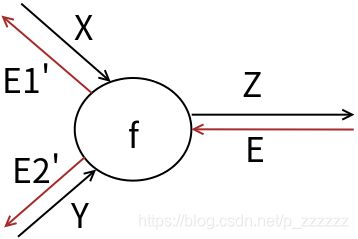
 该图中，计算节点f有了x和y两个输入，即：
$$z=f(x,y)$$
 则反向信号为E时，应该计算局部偏导数乘以反向输入信号作为反向计算的输出，即：
$$E{1}^{\prime }=E\times \frac{\partial Z(x,y)}{\partial x}$$

$$E{2}^{\prime }=E\times \frac{\partial Z(x,y)}{\partial y}$$

 同理，无论正向传播的结构是怎样的，都只需要计算局部偏导数即可。
 以加法节点为例：

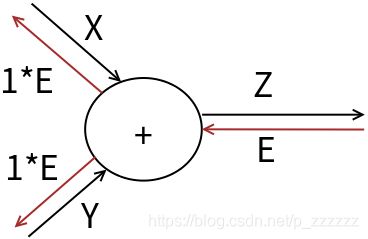
 图中的计算节点为加法，即：
$$z=x+y$$
则，计算局部偏导数有：
$$\frac{\partial (x+y)}{\partial x}=1$$
$$\frac{\partial (x+y)}{\partial y}=1$$
 所以反向传播的结果如图中所示。

 再看看乘法节点的示例：

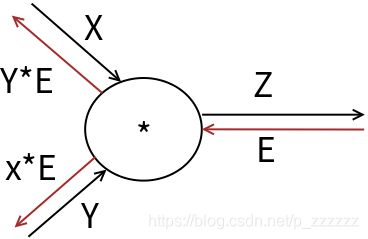
 图中的计算节点为乘法，即：
$$z=x\times y$$
则，计算局部偏导数有：
$$\frac{\partial (x\times y)}{\partial x}=y$$
$$\frac{\partial (x\times y)}{\partial y}=x$$
所以计算结果如图中所示。

简单层的实现

 既然知道了反向传播算法的基本原理，现在我们将反向传播算法带入到神经网络中，实现神经网络中最基本的单位——层。
 我们将构建神经网络中的层实现为一个类。层指的是神经网络中的功能单位，比如sigmoid层指的是负责进行sigmoid计算等。层的实现中，除了层的构造方法外，还应当有一个forward()方法和一个backward()方法，分别用于该层的正向传播和反向传播。

class AddLayer:
	def __init__(self):
		pass

	def forward(self,x,y):
		return x+y

	def backward(self,dout):
		dx = dout *1
		dy = dout *1
		return dx,dy
	
class MulLayer:
	def __init__(self):
		self.x = None
		self.y = None

	def forward(self,x,y):
		self.x = x
		self.y = y
		return self.x *self.y

	def backward(self,dout):
		dx = dout * self.y
		dy = dout * self.x
		return dx,dy

 如上代码中我们实现了一个加法层和一个乘法层，我们用实现的加法层和乘法层对下图进行正向传播和反向传播：

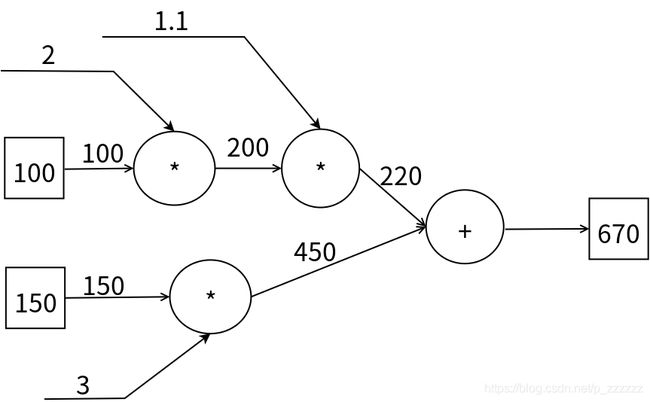
if __name__ == '__main__':
	x = 100
	a1 = 2
	a2 = 1.1
	y = 150
	b1 =3
	mx_a1 = MulLayer()
	mxa1_a2 = MulLayer()
	my_b1 = MulLayer()
	axy = AddLayer()
	
	#正向传播
	x_a1 = mx_a1.forward(x,a1)
	y_b1 = my_b1.forward(y,b1)
	xa1_a2 =mxa1_a2.forward(x_a1,a2)
	xy = axy.forward(xa1_a2,y_b1)
	print(xy)
	#输出结果670.

	#反向传播
	z = 1
	dxa1a2,dyb1 = axy.backward(z)
	print(dxa1a2,dyb1)
	#输出结果是：1 1
	dxa1,da2 = mxa1_a2.backward(dxa1a2)
	print(dxa1,da2)
	#输出结果是：1.1 200
	dx,da1 = mx_a1.backward(dxa1)
	print(dx,da1)
	#输出结果是：2.2 110.00000000000001
	dy,db1 = my_b1.backward(dyb1)
	print(dy,db1)
	#输出结果是：3 150

 以上示例中，我们使用实现的简单层完成了一个计算图的正向传播和反向传播，在神经网络中，误差的反向传播算法表示的是输出层的产生的误差（损失函数的结果）反向传入网络中，通过反向传播算法计算出每个参数对误差的梯度，由此来调整参数值来达到学习的效果。

激活函数层的实现

 现在我们来实现神经网络中存在的层，首先是两个激活函数层——ReLU层和Sigmoid层。
 ReLu层是一个单变量层，其向前传播的数学表达为：
$$y=\{\begin{array}{c}xx(>0)\\ 0x(⩽0)\end{array}$$
 则求出y关于x的导数为：
$$y=\{\begin{array}{c}1x(>0)\\ 0x(⩽0)\end{array}$$
 由以上的数学表达，我们可以如下实现ReLU层。

class ReLU:
	def __init__(self):
		self.mask = None

	def forward(self,x):
		self.mask = (x<=0)
		out = x.copy()
		out[self.mask] = 0
		return out

	def backward(self,dout):
		dout[self.mask] = 0
		dx = dout
		return dx

 Sigmoid层同样是一个单变量层，但是它的数学形式比ReLU函数较复杂：
$$y=\frac{1}{1+exp(-x)}$$
对该函数的求导需要用到一些链式求导技巧：
$$\frac{\partial y}{\partial x}=y^{2}exp(-x)=y(1-y)$$
 由以上的数学表达，可以将Sigmoid层实现为：

class Sigmoid:
	def __init__(self):
		self.out = None

	def forward(self,x):
		out = 1/(1+np.exp(-x))
		self.out = out
		return out

	def backward(self,dout):
		dx = dout * (1.0-self.out)* self.out

仿射层与输出层的实现

 在神经网络的正向传播中，为了计算加权信号的总和，使用了矩阵乘积运算，这在几何邻域中称为仿射变换，因此，将进行仿射变换的处理实现称为仿射层或Affine层也常常被称为全连接层。
 仿射层的正向传播的数学表达为：
$$\mathbf{Y}=\mathbf{X}\cdot \mathbf{W}+\mathbf{B}$$
 则其反向传播的数学表达为：
$$\frac{\partial \mathbf{Y}}{\partial \mathbf{X}\mathbf{Y}}=1$$
$$\frac{\partial \mathbf{Y}}{\partial \mathbf{B}}=1$$
$$\frac{\partial \mathbf{X}\mathbf{Y}}{\partial \mathbf{X}}={\mathbf{W}}^T$$
$$\frac{\partial \mathbf{X}\mathbf{Y}}{\partial \mathbf{W}}={\mathbf{X}}^T$$
 由以上，可以将Affine层实现为：

class Affine:
	def __init__(self,W,b):
		self.W = W
		self.b = b
		self.x = None
		self.dW = None
		self.db = None

	def forward(self,x):
		self.x = x
		out = np.dot(x,self.W) + self.b
		return  out

	def backward(self,dout):
		dx = np.dot(dout,self.W.T)
		self.dW = np.dot(self.x.T,dout)
		self.db = np.dot(dout,axis=0)
		

 对于输出层，我们会使用softmax函数或恒等函数，同时，往往会在输出层后添加一个损失函数的计算，我们将Softmax函数和交叉熵误差函数合并在同一层中实现，称为Softmax-with-Loss层。
 我们这里不加证明的给出Softmax-with-Loss层的反向传播结果（整个证明过程有点麻烦，但实际上也就是较为复杂的复合函数求导）：Softmax层的输入假设为(a₁,a₂,…,a_n)，Softmax层的输出为(y₁,y₂,…,y_n)，监督数据t为（t₁,t₂,…,t_n)，则如果反向输入为1，则整个Softmax-with-Loss层的输出为（y₁ - t₁,y₂ - t₂,…y_n - t_n)，需要注意的是，之所以整个Softmax-with-Loss层的反向传播结果形式这么简单是由于交叉熵函数作为损失函数，是专门设计出来为了使得反向传播的结果形式变得简单的。

Softmax-with-Loss层的实现为：

class SoftWithLoss:
	def __init__(self):
		self.loss = None
		self.y = None
		self.t = None

	def forward(self,x,t):
		self.t = t
		self.y = softmax(x)
		self.loss = cross_entropy_error(self.y,self.t)
		return self.loss

	def backward(self,dout=1):
		batch_size = self.t.shape[0]
		dx = (self.y - self.t)/batch_size
		return dx

 至此，我们已经实现了很多神经网络中的层，已经有了足够充足的砖头，只要将其堆砌起来就可以完成一个既可以向前传播进行预测，又可以向后传播进行学习的神经网络，书中实现了一个简单的二层神经网络：

class TwoLayerNet:
	def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
		self.params = {}
		self.params['W1'] = weight_init_std * np.random.randn(input_size,hidden_size)
		self.params['b1'] = np.zeros(hidden_size)
		self.params['W2'] = weight_init_std * np.random.randn(hidden_size,output_size)
		self.params['b2'] = np.zeros(output_size)

		self.layers = OrderedDict()
		self.layers['Affine1'] = Affine(self.params['W1'],self.params['b1'])
		self.layers['Relu1'] = ReLU()
		self.layers['Affine2'] = Affine(self.params['W2'],self.params['b2'])
		self.lastLayer = SoftmaxWithLoss()

	def predict(self,x):
		for layer in self.layers.values():
			x = layer.forward(x)
		return x

	def loss(self,x,t):
		y = self.predict(x)
		return  self.lastLayer.forward(y,t)

	def gradient(self,x,t):
		#要使用向后传播算法必须有向前传播的结果，即必须产生误差。
		self.loss(x,t)

		dout = 1
		dout = self.lastLayer.backward(dout)

		layers = list(self.layers.values())
		layers.reverse()
		for layer in layers:
			dout = layer.backward(dout)

		grads= {}
		grads['W1'] = self.layers['Affine1'].dW
		grads['b1'] = self.layers['Affine1'].db
		grads['W2'] = self.layers['Affine2'].dW
		grads['b2'] = self.layers['Affine2'].db

		return grads

 代码中没有包含精度计算和数值微分验证的实现。