机器学习笔记1——经验误差、模型评估方法和性能度量
关于模型的评估
文章目录
- 关于模型的评估
-
-
- 经验误差
-
-
- 错误率
- 经验误差
- 过拟合和欠拟合
-
- 模型评估方法
-
-
- 留出法
- 交叉验证法
- 交叉验证的特例——留一法
- 自助法
-
- 性能度量
-
-
- 精度和错误率
- 查全率和查准率
- 受试者工作特征——ROC曲线
- 代价敏感错误率和代价曲线
- 期望总体代价和代价曲线
-
-
经验误差
错误率
m个样本,a个分类错误,错误率: E = a / m E=a/m E=a/m;
经验误差
学习器在训练集上的误差叫做经验误差或者训练误差;
新样本上的误差叫做泛化误差;
并不是正确率越高,学习器就越好;
过拟合和欠拟合
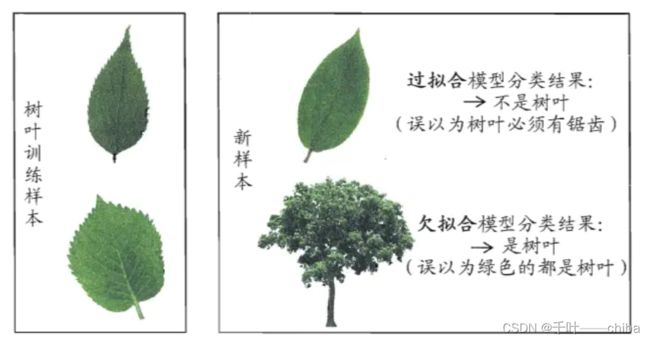
过拟合:学习器将训练样本学习的太好了,导致很多训练样本自身的特点当作了所有潜在样本的一般性质(训练误差小泛化误差大);
欠拟合:训练样本的一般性质都没有学号,训练误差大;
下图直观说明(图源:机器学习西瓜书):
欠拟合一般可以避免,但是过拟合基本是无法避免的,只能说是减少它带来的影响;
模型评估方法
测试集尽量要跟训练集互斥;
留出法
将数据集划分为两个互斥集合,一个作为训练集,一个作为测试集;通常将2/3~4/5的样本用于训练,剩余用作测试;
要注意:需要通过分层采样的方法保证数据的分布一致性;
为了保持训练正确率和普适性,我们可以进行n次划分评估,最后求出n次结果的均值;
交叉验证法
将数据集划分为很多(n)个大小相似的互斥子集,然后进行n次循环(如下图所示):
- 每次选取第i个集合作为测试集,剩余子集的并集作为训练集( i ∈ [ 1 , n ] i \in [1,n] i∈[1,n]);
- 循环k次,每次选取不同的集合作为测试集,最后返回k次测试的均值;
- 评估结果的稳定性取决于k的数量,一般k取值为10;
交叉验证的特例——留一法
-
数据集中有n个样本,进行k次划分,当k=n时,n个样本的划分方式是唯一的,每个划分出来的子集只有一个元素;
-
之所以叫留一法,因为这种方法是在每次测试中只留一个样本作为测试集;
-
由于留一法的训练集跟初始数据集只差一个样本,因此留一法的评估结果往往比较准确;
-
缺点是计算开销有可能很大,因为数据量庞大起来,划分的次数也会跟着变大;
自助法
- 给定一个包含n个样本的数据集D,和一个采样集T,T初始为空;
- 每次从D中选择一个样本,复制进T中,也许会出现某一个已经被采集的样本再次被采集;
- 重复第二步n次,得到最终的采样集T,将T作为训练集,D\T作为测试集;
每个样本从始至终不被采集的概率为 lim m → ∞ ( 1 − 1 m ) m = 1 e \lim_{m \to \infty}{(1- \frac{1}{m})^m} = \frac{1}{e} limm→∞(1−m1)m=e1;
也就是说,每个样本都有大约 1 3 \frac{1}{3} 31的概率不被采集到并作为测试集;从概率宏观的角度来说,也就是我们把约 1 3 \frac{1}{3} 31的样本当作了测试集;
自助法适用于数据集规模较小或者在划分训练\测试集的时候比较有用,也可以从初始数据集中产生多个不同的数据集;但是这种方法会改变初始数据集的分布(因为每次抽取具有随机性,无法确保分层取样等),因此会有估计误差;所以在数据量足够的时候用前面两种方法会更好。
性能度量
精度和错误率
这两个指标既适用于二分类任务,也适用于多分类任务。
假设给定一个样例集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) D={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)} D=(x1,y1),(x2,y2),...,(xn,yn),其中 y i y_i yi为 x i x_i xi的真实分类结果, f ( x i ) f(x_i) f(xi)为学习器预测的结果;
错误率指的就是分类错误的样本数占总样本数的比例,定义如下:
E ( f ; D ) = 1 m ∑ i = 1 m ∥ ( f ( x i ) ≠ y i ) E(f;D)= \frac{1}{m} \sum_{i=1}^{m} \parallel(f(x_i) \neq y_i) E(f;D)=m1i=1∑m∥(f(xi)=yi)在回归方法中,错误率常用均方误差来表示:
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f;D)= \frac{1}{m} \sum_{i=1}^{m} (f(x_i) - y_i)^2 E(f;D)=m1i=1∑m(f(xi)−yi)2精确度的定义即为: 1 − E ( f ; D ) 1-E(f;D) 1−E(f;D);
查全率和查准率
错误率并不能满足所有的任务需求,因此我们引入查全率和查准率两个概念;
例如对搜索引擎好坏的判定,假设用户某一个查询的正确信息(我们可以理解为可以满足用户查询需求的信息集合)的总集合为D,该搜索引擎为我们返回的信息的集合为S,我们需要关心的主要有两个问题:
- S中有多少信息在D中?
- D中有多少信息在S中?
第一个问题,就是我们需要判定搜索引擎返回的正确信息所占的返回总信息数(|S|)的比例,这就是查准率;
如果返回的结果很少,那光有上面这一个指标是不行的,因此我们还要考虑第二个问题,即这个搜索引擎总共能返回多少个正确的信息,这就是查全率;
通过上面的例子,我们可以理解到,这两个指标,一般用于二分类问题中,接下来再看一个例子:
| 真实情况 | 检索出的结果 | 被搜索引擎抛弃的结果 |
|---|---|---|
| 正确信息 | TP(真正例) | FN(假反例) |
| 错误信息 | FP(假正例) | TN(真反例) |
一个搜索引擎检索出的结果可能有真正正确的(TP),实际上不正确的(FP),那么根据查准率的定义,查准率P的计算公式为:
P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
真正正确的信息中,有被搜索引擎检索出来的(TP),也有被抛弃的(FN),因此查全率的公式为:
R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
查全率和查准率是两个矛盾的指标,因为如果为了查全率而把查询数量加大,那么查准率会下降,因此,我们引入PR曲线来直观表述这两个指标,进而对学习器性能进行一个描述(图源西瓜书);

A曲线和B曲线完全把C曲线“包住”了,因此我们可以判定A和B学习器要优于C;但是A和B之间,有一个交叉点,在查全率高的时候B要强一些,反之A强一些,很难断言谁更强。
因此我们引入平衡点的概念:当P=R的时候,谁的PR值更高谁就相对强一些:A的平衡点PR值更高,因此可以认为A相对于B要好一些。
但是这个评价还是不够客观,因为我们已经默认查全率和查准率的重要性是一样的。实际应用中,根据不同需求,查全率和查准率的重要性往往不一样,比如淘宝推荐中,查准率会更加重要。因此我们需要设置一个加权评判标准:
F β = ( 1 + β 2 ) × P × R β 2 × P + R F_{\beta}=\frac{(1+\beta^2)×P×R}{\beta^2×P+R} Fβ=β2×P+R(1+β2)×P×R
当 β \beta β小于1的时候,对查准率有更大的影响;反之对查全率有比较大的影响;
当 β \beta β等于1的时候,这个公式等价为标准 F 1 F1 F1度量方法:
F 1 = 2 × P × R P + R = 2 × T P N + T P − T N F_1=\frac{2×P×R}{P+R}=\frac{2×TP}{N+TP-TN} F1=P+R2×P×R=N+TP−TN2×TP
其中 N N N为样例总数;
受试者工作特征——ROC曲线
这是查全率和查准率的一个延申,思路就是用于个分类阈值来进行二分类,主要用于神经网络的计算结果进行分类;
神经网络一般预测值都在0-1之间,设置一个在0-1之间的阈值a,大于a则判定为正类,反之为反类;
拿查重率和查准率来说,如果我们希望查准率更加重要,,参照之前讲过的PR曲线,那么我们可以把这个阈值设置的更加小一些;同理,如果我们希望查全率更加重要,那么我们就把阈值设置的更大;
ROC曲线,就是用来判断这种“学习器的期望泛化性能的好坏”的一个工具,概念理解起来有点困难,先看下面的步骤就可以懂了;
首先把上面的表格搬下来:
真实情况 检索出的结果 被搜索引擎抛弃的结果 正确信息 TP(真正例) FN(假反例) 错误信息 FP(假正例) TN(真反例) 定义两个概念:
- 命中率: T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP;
- 虚惊率: F P R = F P T N + F P FPR=\frac{FP}{TN+FP} FPR=TN+FPFP(找到的反例中占所有反例的比例);
针对训练结果,我们按照预测值排序;
接下来,以FPR为横坐标,TPR为纵坐标绘制一个折线图,类似下图:

绘图过程大致如下:
- 给定m个正例和n个反例,按照机器学习的结果排序,得到序列 s 1 , s 2 , . . . , s m + n {s_1,s_2,...,s_{m+n}} s1,s2,...,sm+n;
- 先把分类阈值设为最大,即所有的样例都设为反例,这个时候TP=0,因此命中率和虚惊率都是0,再坐标原点处画一个点;
- 此后将阈值设置为每个样例的预测值,计算各自的命中率和虚惊率,得到对应的坐标点 ( x i , y i ) (x_i,y_i) (xi,yi),在图上画出;
- 最后点连成线,如果曲线包络的面积越大,说明这个学习器分类分的越好,质量就越高;
所以,从上面的过程我们可以看出,这其实是一个查全率和查准率的一个延申应用。为了提高查全率,我们肯定需要增加样本数量,那么如果我的学习器在提升样本数量的同时(虚惊率也会因此而提升),我的命中率如果越来越高,说明我这个学习器就越好。
如果要利用ROC曲线来定量的表示两个学习器的性能,有如下两种方法:
-
寻找最优零界点:寻找 m a x ( T P R − F P R ) max(TPR-FPR) max(TPR−FPR)所对应的阈值,这个点越在图的左上方就说明ROC曲线越优;
-
面积法(AUC):比较两个曲线和x轴、图的右半边竖线围成的面积大小,可利用如下公式计算:
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ∗ ( y i + y i + 1 ) AUC=\frac{1}{2} \sum_{i=1}^{m-1}(x_{i+1}-x_i)*(y_i+y_{i+1}) AUC=21i=1∑m−1(xi+1−xi)∗(yi+yi+1)
AUC的值越大,就说明学习器越优;
代价敏感错误率和代价曲线
以二分类问题为例,分类错误主要有两种情况:
- 把一部分假的信息当作真信息返回(假正例);
- 把一部分真的信息当作家的信息舍弃(假反例);
在实际应用中,我们对于两种错误的付出的代价是完全不一样的,比如一个门禁系统,把可通行用户拦在门外和把不可通行用户放进去造成的潜在后果是不一样的。而前面的算法中,我们都是假设了均等错误代价,把错误率直接计算成错误次数,没有考虑不同错误造成的后果。因此,我们需要针对两种错误类别,再做一次加权。
假设一个样例集合D中,正例子集为T,反例子集为F;假正例导致的代价为 c o s t 10 cost_{10} cost10,假反例导致的代价为 c o s t 01 cost_{01} cost01;
对错误率公式进行加权得到代价敏感错误率:
E ( f ; D ; c o s t ) = 1 m ( ∑ x i ∈ T ∥ ( f ( x i ) ≠ y i + ∑ x i ∈ F ∥ ( f ( x i ) ≠ y i ) E(f;D;cost)=\frac{1}{m}(\sum_{x_i \in T}\parallel(f(x_i) \neq y_i+\sum_{x_i \in F}\parallel(f(x_i) \neq y_i) E(f;D;cost)=m1(xi∈T∑∥(f(xi)=yi+xi∈F∑∥(f(xi)=yi)
当公式中i和j取值不限于0和1的时候,该公式可以改写为多分类问题的代价敏感错误率公式;
同样的,ROC曲线也没有考虑代价的问题,而代价曲线就考虑了,过程如下:
首先引入第一概念叫做加权正例概率,应该还是比较好理解的:
P c o s t = p × c o s t 01 p × c o s t 01 + ( 1 − p ) × c o s t 10 P_{cost}=\frac{p×cost_{01}}{p×cost_{01}+(1-p)×cost_{10}} Pcost=p×cost01+(1−p)×cost10p×cost01
其中p表示查准率,即样例为正例的概率;
第二个概念叫做归一化代价,先上公式:
c o s t t o r m = ( 1 − T P R ) × p × c o s t 01 + F P R × ( 1 − p ) × c o s t 10 p × c o s t 01 + ( 1 − p ) × c o s t 10 cost_{torm}=\frac{(1-TPR)×p×cost_{01}+FPR×(1-p)×cost_{10}}{p×cost_{01}+(1-p)×cost_{10}} costtorm=p×cost01+(1−p)×cost10(1−TPR)×p×cost01+FPR×(1−p)×cost10
公式中的TPR和FPR就是ROC中的命中率和虚惊率,那么 ( 1 − T P R ) (1-TPR) (1−TPR)就是没有被选中的真信息的比率,也就是假反例占总正例的比率;整个计算式,就是对 ( 1 − T P R ) (1-TPR) (1−TPR)和 F P R FPR FPR两者进行了一个加权运算,获得的结果我们可以理解为两类错误的平均加权代价。
把加权正例概率作为横坐标,归一化代价作为纵坐标,即可得出代价曲线;
期望总体代价和代价曲线
将ROC中每个点的两个量 ( 1 − T P R ) (1-TPR) (1−TPR)和 F P R FPR FPR计算出来,然后在代价平面上绘制一条从 ( 0 , F P R ) (0,FPR) (0,FPR)到 ( 1 , 1 − T P R ) (1,1-TPR) (1,1−TPR)的线段,如此遍历所有的ROC点,可以得到一幅类似下图的图像(图源西瓜书):
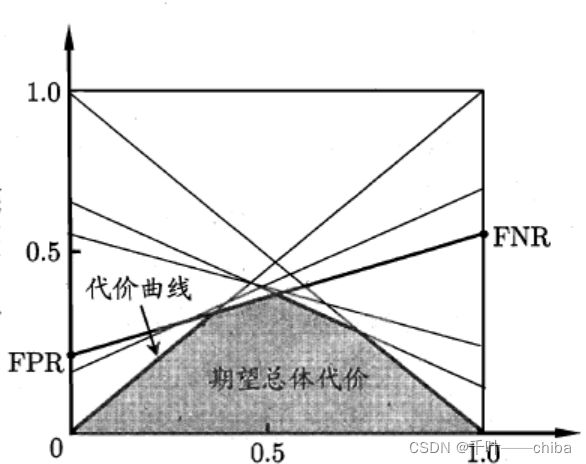
阴影部分即为期望总体代价,围成这一部分的折线即为代价曲线。跟上面一小节一对比,我们可以发现,当横坐标为0的时候(即p=0), c o s t t o r m cost_{torm} costtorm可以视为 F P R FPR FPR,而当横坐标为1的时候(p=1), c o s t t o r m cost_{torm} costtorm可以视为 1 − T P R 1-TPR 1−TPR,即图中的 F N R FNR FNR。
在面对考虑代价的学习模型的时候可以参考使用这两种方法,这两种方法其实从本质上看是同一种思路的不同执行方法而已,选择哪种视具体情况而定。
下一节:机器学习笔记2——比较检验