Python深度学习入门笔记 4 CNN
Python深度学习入门笔记 4 CNN
卷积神经网络
这一部分的主题是卷积神经网络CNN。
网络结构
CNN和之前介绍的神经网络一样,也是一层一层构建,不过,CNN中新出现了卷积层(Convolution层)和池化层(Pooling层)。
在之前介绍的神经网络中,相邻层的所有神经元之间都有连接,这称为全连接(fully-connected),下图是基于全连接层(Affine层)的网络的例子:
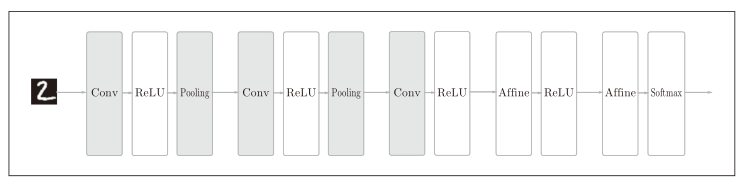
而CNN的结构通常是:
在CNN中,层的连接顺序是“Convolution-ReLU-(Pooling)”(Pooling 层有时会被省略)。这可以理解为之前的“Affine-ReLU”连接被替换成了“Convolution-ReLU-(Pooling)”连接。不过,靠近输出层的部分还是使用了之前的“Affine-ReLU”,输出层也使用的是“Affine-Softmax”
卷积层
全连接层有什么问题?
全连接层存在一个问题:数据的形状被“忽视”了,例如,输入图片时,通常的图片数据都是“高、长、通道“方向上的三维数据,但是,向全连接层输入时,需要将3维数据拉平为1维数据。
在图像的这个三维数据中,存在着重要的空间信息,比如,空间上邻近的像素为相似的值、RBG的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等,3维形状中可能隐藏有值得提取的本质模式。因为全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一维度的神经元)处理,所以无法利用与形状相关的信息。
而卷积层可以保持形状不变。当输入数据是图像时,卷积层会以 3 维数据的形式接收输入数据,并同样以3 维数据的形式输出至下一层。因此,在CNN中,可以(有可能)正确理解图像等具有形状的数据。
在CNN 中,有时将卷积层的输入输出数据称为特征图(feature map)如,输入特征图,输出特征图。后续“输入输出数据”和“特征图”将表示同样的意思。
关于后续会涉及一些数字图像处理中的名词和知识,我之前的分享中有详细的整理,数字图像处理笔记。
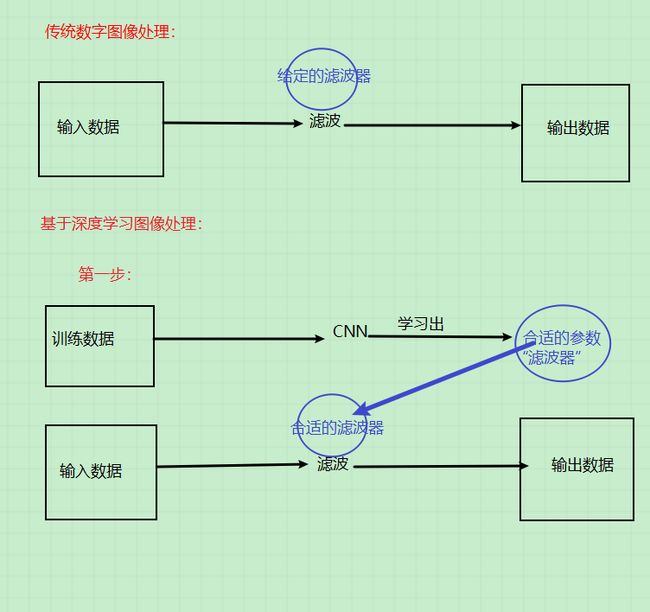
传统数字图像处理和基于深度学习的图像处理之间最主要的差别在于:传统数字图像处理中用到的滤波器是固定的,比较通用的,或者是根据经验研究已经确定好的;而基于深度学习可以“学习出”针对当前场景最合适的滤波器。除此之外,对于图像的处理操作,二者是没有什么差别的。
简化一下就如下图所示:
卷积运算
卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的“滤波器运算”。“滤波器”也叫作“核”。
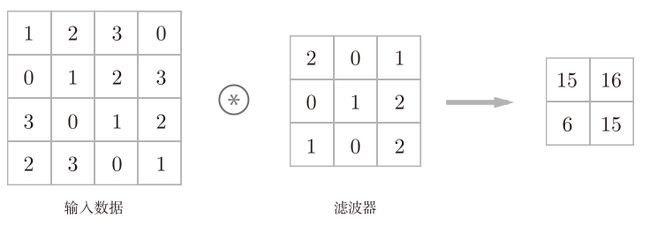
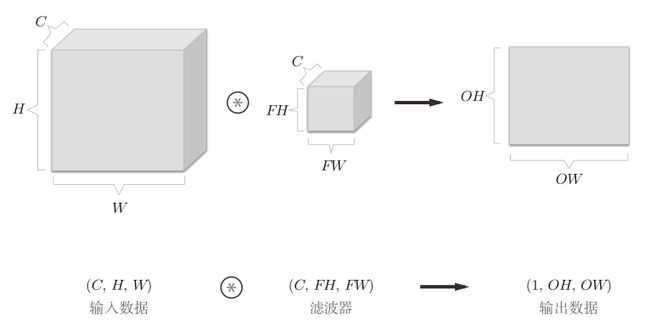
一个输入数据大小是(4, 4),滤波器大小是(3, 3),最终输出大小的(2, 2)的例子:
对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用,将各个位置上滤波器的元素和输入的对应元素相乘,然后再求和(有时将这个计算称为乘积累加运算)。然后,将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍,就可以得到卷积运算的输出。
CNN中,滤波器的参数就对应之前的权重。并且,CNN中也存在偏置。偏置通常只有1个,这个值会被加到应用了滤波器的所有元素上。
填充
可以看到的是,经过滤波之后,图像比之前“少了一圈”,那是因为图像最外层的元素没有完整的四周元素与滤波器对应相乘。我们为了是边缘元素不会丢失,就采用了填充。
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比
如0等),这称为填充(padding)。
卷积运算的填充处理:向输入数据的周围填入0(图中用虚线表示填充,0没有显示出来)
步幅
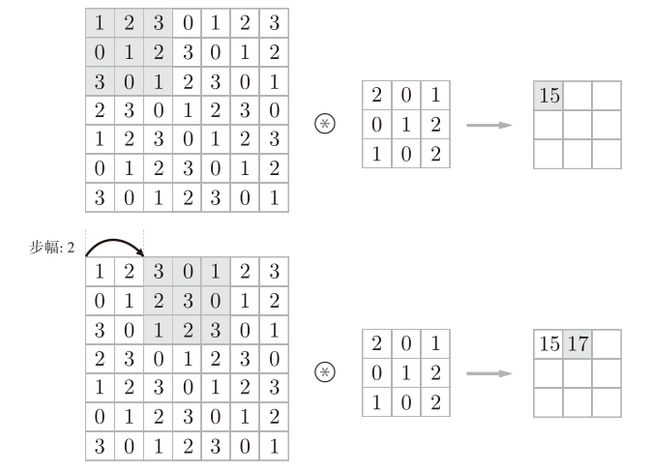
应用滤波器的位置间隔称为步幅(stride)。如果将步幅设为2,则如下图所示,应用滤波器的窗口的间隔变为2个元素。
综上,增大步幅后,输出大小会变小。而增大填充后,输出大小会变大。那么如何通过二者与输入大小计算出输出大小呢?
假设输入大小为(H, W),滤波器大小为(FH, FW),输出大小为(OH, OW),填充为P,步幅为S,那么输入大小就是:
注意式子中的除法,当输出大小无法除尽时(结果是小数时),需要采取报错等对策。
3维数据的卷积运算
我们来看一下对加上了通道方向的3维数据进行卷积运算的例子。
注意:在3维数据的卷积运算中,滤波器的通道数只能设定为和输入数据的通道数相同的值。
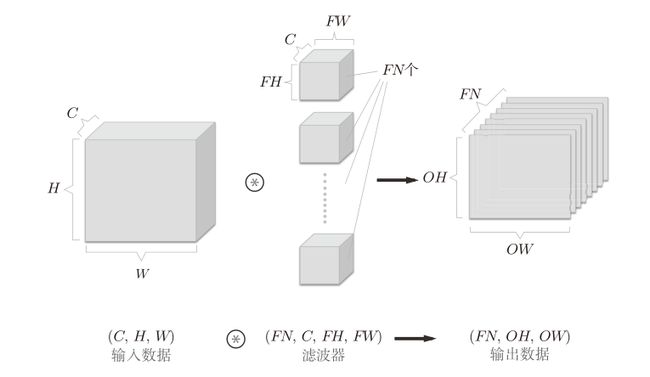
到这里,我们又发现一个问题:三维数据经过一个滤波器滤波后变成了二维数据。
怎么解决呢?**用多个滤波器(权重)**就可以了。
通过应用FN个滤波器,输出特征图也生成了FN个。如果将这FN个特征图汇集在一起,就得到了形状为(FN, OH, OW)的方块。将这个方块传给下一层,就是CNN的处理流。
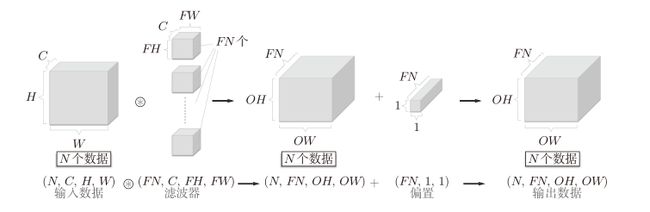
每个通道有一个偏置,因此,偏置的形状是 (FN, 1, 1)。
批处理
神经网络的处理中进行了将输入数据打包的批处理。如果我们希望卷积运算也同样对应批处理,就需要将在各层间传递的数据保存为4维数据(一批三维数据)。具体地讲,就是按(batch_num, channel, height, width)的顺序保存数据。
池化层
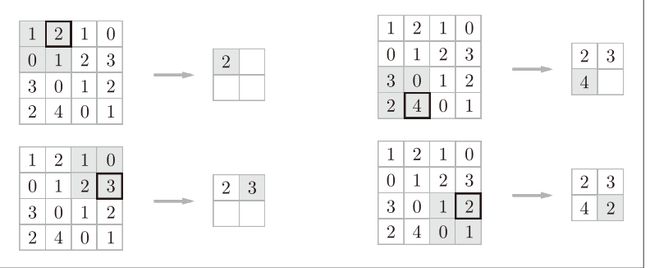
池化是缩小高、长方向上的空间的运算。在图像识别领域,主要使用Max池化,也就是说选取一个目标区域里的最大值。
下面例子是按步幅2进行2 × 2的Max池化时的处理顺序:
池化层的特征:
- 没有要学习的参数,它的工作很简单只是从目标区域中取最大值(或者平均值),所以不存在要学习的参数。
- 通道数不发生变化,每个通道单独池化。
- 对微小的位置变化具有鲁棒性(健壮)。
卷积层和池化层的实现
我们将用Python来实现这两个层,不过在开始之前我们还要解决一些小问题。
基于im2col的展开
CNN中处理的是4维数据,因此卷积运算的实现看上去会很复杂,但是通过使用im2col,问题就会变得很简单。
如果老老实实地实现卷积运算,估计要重复好几层的for语句。这样的实现有点麻烦,而且,NumPy中存在使用for语句后处理变慢的缺点(NumPy中,访问元素时最好不要用for语句)
im2col(image to column)是一个函数,将输入数据展开以适合滤波器(权重)。
在上图中,为了便于观察,将步幅设置得很大,以使滤波器的应用区域不重叠。而在实际的卷积运算中,滤波器的应用区域几乎都是重叠的。在滤波器的应用区域重叠的情况下,使用im2col展开后,展开后的元素个数会多于原方块的元素个数。因此,使用im2col的实现存在比普通的实现消耗更多内存的缺点。但是,汇总成一个大的矩阵进行计算,对计算机的计算颇有益处。
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
filter_h : 滤波器的高
filter_w : 滤波器的长
stride : 步幅
pad : 填充
Returns
-------
col : 2维数组
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
使用im2col展开输入数据后,之后就只需将卷积层的滤波器(权重)纵向展开为1列,并计算2个矩阵的乘积即可。
可以看到,展开之后正好可以利用矩阵的乘法进行计算。
卷积层的实现
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中间数据(backward时使用)
self.x = None
self.col = None
self.col_W = None
# 权重和偏置参数的梯度
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
# 计算输出数据大小
out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
out_w = int(1 + (W + 2*self.pad - FW) / self.stride)
# 输入数据展开
col = im2col(x, FH, FW, self.stride, self.pad)
# 滤波器的展开
col_W = self.W.reshape(FN, -1).T
# 使用矩阵乘法计算
out = np.dot(col, col_W) + self.b
# 重新变为三维的形状
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
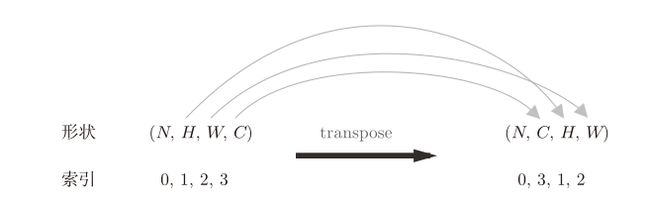
这里要注意,通过在reshape时指定为-1,reshape函数会自动计算-1维度上的元素个数,以使多维数组的元素个数前后一致。而transpose会更改多维数组的轴的顺序,例如transpose(0, 3, 1, 2)就是将原来0,1,2,3位置的轴分别换到输入参数的位置。
以上就是卷积层的forward处理的实现。至于卷积层的反向传播的代码,用到了col2im,就是im2col的逆过程。代码如下:
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col :
input_shape : 输入数据的形状(例:(10, 1, 28, 28))
filter_h :
filter_w
stride
pad
Returns
-------
"""
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
池化层的实现
池化的应用区域按通道单独展开。
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
#展开
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h * self.pool_w)
#最大值
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
#转换
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
最大值的计算可以使用 NumPy 的np.max方法。np.max可以指定axis参数,并在这个参数指定的各个轴方向上求最大值。比如,如果写成np.max(x, axis=1),就可以在输入x的第1维的各个轴方向上求最大值。
通过将输入数据展开为容易进行池化的形状,后面的实现就会变得非常简单.
CNN的实现
将要实现的网络的构成是“Convolution-ReLU-Pooling-Affine-
ReLU-Affine-Softmax”,我们将它实现为名为SimpleConvNet的类
class SimpleConvNet:
"""
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_size : 输入大小(MNIST的情况下为784)
hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100])
output_size : 输出大小(MNIST的情况下为10)
activation : 'relu' or 'sigmoid'
weight_init_std : 指定权重的标准差(e.g. 0.01)
指定'relu'或'he'的情况下设定“He的初始值”
指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
"""
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
#计算卷积层输出数据大小
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
#计算池化层输出数据大小
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
#输出层单独放置
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
参数x是输入数据、t是教师标签
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def numerical_gradient(self, x, t):
"""求梯度(数值微分)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
loss_w = lambda w: self.loss(x, t)
grads = {}
for idx in (1, 2, 3):
grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
"""求梯度(误差反向传播法)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
除了网络结构中使用了卷积层和池化层外,可以看到,cnn的实现代码的主要流程和之前使用全链接层实现的神经网络没有什么区别。
CNN的可视化
CNN中用到的卷积层在“观察”什么呢?
下图展示的是学习前和学习后的第1层的卷积层的权重,权重的元素是实数,但是在图像的显示上,统一将最小值显示为黑色(0),最大值显示为白色(255):
学习前的滤波器是随机进行初始化的,所以在黑白的浓淡上没有规律可循,但学习后的滤波器变成了有规律的图像。我们发现,通过学习,滤波器被更新成了有规律的滤波器。
如果要问图中右边学习过的有规律的滤波器在“观察”什么,答案就是它在观察边缘(颜色变化的分界线)和斑块(局部的块状区域)等。
在传统数字图像处理中,检测边缘的滤波器一般都是固定的,如梯度算子,高斯-拉普拉斯算子等。而神将网络可以根据训练图像自己学习出边缘的规律,产生合适的滤波器。
基于分层结构的信息提取
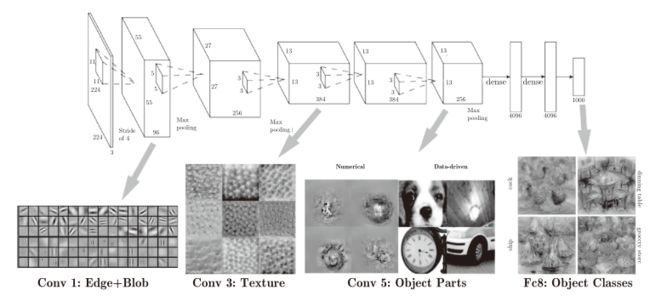
根据深度学习的可视化相关的研究,随着层次加深,提取的信息(正确地讲,是反映强烈的神经元)也越来越抽象。
CNN的卷积层中提取的信息。第1层的神经元对边缘或斑块有响应,第3层对纹
理有响应,第5层对物体部件有响应,最后的全连接层对物体的类别(狗或车)有
响应。
如果堆叠了多层卷积层,则随着层次加深,提取的信息也愈加复杂、抽象,这是深度学习中很有意思的一个地方。随着层次加深,神经元从简单的形状向“高级”信息变化。换句话说,就像我们理解东西的“含义”一样,响应的对象在逐渐变化。
具有代表性的CNN
LeNet
LeNet是最早的CNN,和“现在的CNN”相比,LeNet有几个不同点:
- 第一个不同点在于激活函数。LeNet 中使用sigmoid 函数,而现在的 CNN中主要使用 ReLU 函数。
- 原始的LeNet中使用子采样(subsampling)缩小中间数据的大小,而现在的CNN中Max池化是主流。
AlexNet
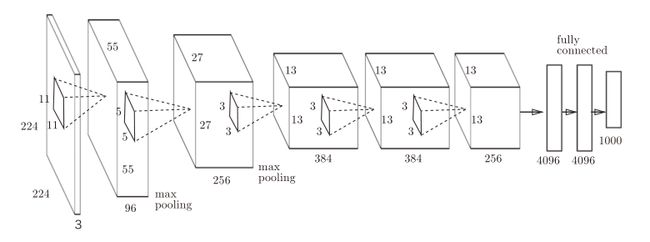
AlexNet是引发深度学习热潮的导火线,不过它的网络结构和LeNet基本上没有什么不同。
AlexNet叠有多个卷积层和池化层,最后经由全连接层输出结果,在结构上AlexNet和LeNet没有大的不同,但有以下几点差异:
- 激活函数使用ReLU。
- 使用进行局部正规化的LRN(Local Response Normalization)层
着层次加深,神经元从简单的形状向“高级”信息变化。换句话说,就像我们理解东西的“含义”一样,响应的对象在逐渐变化。
具有代表性的CNN
LeNet
[外链图片转存中…(img-2DFXyUwG-1642312849109)]
LeNet是最早的CNN,和“现在的CNN”相比,LeNet有几个不同点:
- 第一个不同点在于激活函数。LeNet 中使用sigmoid 函数,而现在的 CNN中主要使用 ReLU 函数。
- 原始的LeNet中使用子采样(subsampling)缩小中间数据的大小,而现在的CNN中Max池化是主流。
AlexNet
AlexNet是引发深度学习热潮的导火线,不过它的网络结构和LeNet基本上没有什么不同。
[外链图片转存中…(img-YSH2M5DR-1642312849110)]
AlexNet叠有多个卷积层和池化层,最后经由全连接层输出结果,在结构上AlexNet和LeNet没有大的不同,但有以下几点差异:
- 激活函数使用ReLU。
- 使用进行局部正规化的LRN(Local Response Normalization)层
- 使用Dropout(在学习的过程中随机删除神经元)。