数据结构系列1------数据结构简介

1.1数据结构

先了解几个基本的概念。

数据(Data)是对信息的一种符号表示，是所有能输入到计算机中并被计算机程序处理的符号的总称。通俗说，凡是能被计算机识别、存储和加工处理的符号，如字符、图形、图像、声音、视频信号等一切信息都可以称为数据，数据是计算机程序的"原料"。

数据元素(Data Element)是数据的基本单位，在程序中通常作为一个整体进行处理。一个数据元素可以有若干个数据项组成。数据项是数据不可分割的最小单位。数据项有时也称为字段或域。

数据对象(Data Object)是性质相同的数据元素的集合，是数据的一个子集。比如整数数据对象的集合可以表示成N={0,±1,±2,….}，字符数据对象集合可以表示为C={'a','b','c'…}。

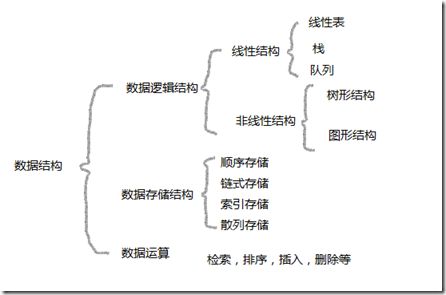
数据结构(Data Structure)是数据元素之间存在的一种或多种特定关系的集合。具体来说，数据结构是按某种逻辑关系组织起来的一批数据。他们按一定表现方式存储在计算机的存储器上，数据结构包括数据逻辑结构、数据存储结构、数据运算。如图：

1：逻辑结构

逻辑结构是数据元素之间的关联方式。数据元素之间的逻辑关系的整体成为逻辑结构。数据逻辑结构是数据的组成方式。

①：线性结构。数据元素之间一对一的线性关系，第一个元素无直接前趋，最后一个元素无直接后趋。其余元素只有惟一的一个前趋和唯一的一个后趋。

②：非线性结构。数据元素之间为一对多或者多对多的非线性关系，每个数据元素有多个直接前趋或者多个直接后趋。

可以分为集合、线性、树形、图状。数据结构(Data Structure)简记DS，是一个二元组，DS=(D,R).其中D是数据元素的有限集合，R是数据元素之间关系的有限集合。

2：数据存储结构

①：顺序存储。每个存储节点只包含一个数据元素。所有存储结点相继存放在一个连续的存储区中。逻辑上相邻的数据元素存放到计算机内存中仍然相邻。借助数据元素在存储器中的相对位置来表示数据元素之间的逻辑关系。用这种方式表示逻辑关系的存储结构称为顺序存储。

②：链式存储。每个存储结点不仅仅含有一个数据元素，也包含一组指针。每个指针指向一个与本节点有逻辑关系的节点。这种存储方式不要求逻辑上相邻的数据元素在物理位置上相邻，数据元素之间的逻辑关系是由附加的指针表示的。

③:索引存储。每个存储结点只包含一个数据元素，所有存储结点连续存放。使用该方式存放时，还需要建立附加的索引表。索引表中的每一项称为索引项(索引)。索引项的一般形式是：(关键字，索引)，其中的关键字是能唯一标识一个节点的数据项，索引指示各存储结点的存储位置或位置区间端点。

④：散列存储。每个存储结点只包含一个数据元素，各个结点均匀的分布在存储区中。该方法的基本思想是通过构造散列函数，根据节点的关键字直接计算出该数据元素的存储地址。

3：数据运算

数据的运算是对数据的操作。运算的定义取决于逻辑结构，运算的实现必须依赖于存储结构。运算只描述处理功能，不包括处理步骤和方法，因此运算实现的核心是处理步骤的规定，即算法的设计。

1.2数据类型

1.数据类型

数据类型(Data Type)是一个值的集合，以及在这个集合上定义一组操作的总称。可以分为：

①：原子类型：值不可分解，如(整形、字符型)、指针类型等

②：结构类型：值可以分解成若干成分，如(数组、结构等)。结构类型的成分可以是原子类型，也可以是某种结构类型。

2：抽象数据类型

抽象数据类型(Abstract Data Type,ADT)是指一个数学模型以及定义在该模型上的一组操作。抽象数据类型的定义取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关。不管其内部结构如何变化，只要它的数学特性不变，都不影响其外部的使用。比如：

求字符串长度、索引位置、合并两个集合、比较、替换等。

1.3算法的特性

算法(Algorithm)是对某一特定类型的问题的求解步骤的描述，应该具备五个特性

1):有穷性(Finity)

2):确定性(Unambiguousness)

3):输入(Input)

4):输出(Output)

5):可行性(Realizability)

算法的评价主要标准为正确性、可读性、健壮性、时间效率、空间存储需求。

1.4算法度量分析

1：时间复杂度分析

对于解决同一个问题的算法，执行时间短的显然比执行时间长的效率高，也就是说执行时间短的比时间长的算法时间复杂度低。估算算法执行时间的最重要的因素是输入算法的数据量(问题规模)。比如在100个单词中查找某个单词与在10W个单词中查找某个单词所花费的时间肯定不同。因此，一个算法的执行时间T可以表示为问题规模n的一个函数T(n)。除了问题规模外，实现算法的程序设计语言、编译后产生的机器码质量、机器执行速度等都会影响执行时间，所以不能把T(n)作为算法的实际执行时间。一般用算法中语句被执行的次数来表示算法的时间效率(时间复杂度)

比如：下面的算法用来求1+2+3+4+….+n

第一种：

int Sum(int n)

{

     int j, sum = 0;

     for (int i = 0; i < n; i++)

     {

         sum = sum + i;

     }

     return sum;

}

以上语句，int j,sum执行1次，for (int i = 0; i < n; i++) 执行n+1次，sum = sum + i; 执行n次，return sum;执行1次。

因此，该算法的时间复杂度T(n)=2n+3，并且随着N的增长，T(n)也随n的比例增长。看看另一种方法

第二种：

int Sum(int n)

{

    int sum = 0;

    sum = (1 + n) * n / 2;

    return sum;

}

以上语句,int sum=0执行一次，sum = (1 + n) * n / 2;执行一次，return sum;执行一次，该算法的时间复杂度T(n)=3，不会随着n的变化而变化

常忽略一些次要语句的执行次数(比如上面的return sum)，只保留重要语句和执行最频繁的语句计数，同时对计算结果中的次要项也忽略，只保留主要项，给出数量级，这种表示方式叫渐进时间复杂度。通常用O表示，定义为：

当且仅当存在正整数c和N，使得对所有n≥N，有T(n)≤cf(n)成立，则称T(n)是O(f(n))。

对于一个算法，假设其问题的输入大小为n，那么我们可以用 O(n) 来表示其算法复杂度(time complexity)。那么，渐进时间复杂度（asymptotic time complexity）就是当n趋于无穷大的时候，O（n）得到的极限值。(来自大百度百科)。

O表示岁问题规模n的增加，算法的时间复杂度T(n)和函数f(n)具有相同的数量级。例如第一种求和方法中，T(n)=O(n),T(n)是n的数量级，因此当n≥2时，有f(n)≤5n，所以可选N=2，c=5。