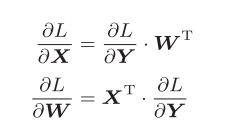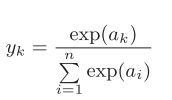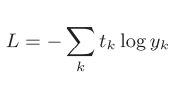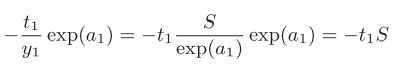深度学习入门-误差反向传播法(人工神经网络实现mnist数据集识别)
文章目录
-
-
-
- 误差反向传播法
-
- 5.1 链式法则与计算图
- 5.2 计算图代码实践
- 5.3激活函数层的实现
- 5.4 简单矩阵求导
- 5.5 Affine 层的实现
- 5.6 softmax-with-loss层计算图推导
- 5.7 softmax-with-loss层的实现
- 5.8 误差反向传播算法的实现
-
-
误差反向传播法
这次用到的代码上传到csdn了,0积分下载误差反向传播代码其实本文也都贴出来了,只是需要改一下import的路径。还有一些数学公式函数数学公式。若理解困难参考上一章节神经网络的学习-搭建神经网络。小白请参考第一章深度学习入门-从朴素感知机到神经网络。
根据《深度学习入门》所写的笔记。简单矩阵求导一节借鉴b站九天Hector的视频。
5.1 链式法则与计算图
复合函数求导的链式法则我们很熟悉,如果我们稍微加一点限制它就会变得很有趣。
我们用计算图的方式来表达一个数学函数,至于什么是计算图,看一眼下图就知道了,我们用节点表示计算符号(加减乘除),并且每个计算符号只有两个输入和一个输出。
我们来看三个例子:(代码非常简单,稍微了解计算机观看代码就能理解误差反向传播)
按箭头方向我们很容易看出来这就是三个函数,z = x + y +w,z = x * y * w,z = x * y + w。
在各条横线下面求出了导数值,我们可以发现一个规律,如果按箭头相反的方向看,例如z = x * y + w的例子,加法后(指向x,y,w方向)的导数值不变 ,乘法后的导数值乘以其翻转值,例如x的导数值是z对t的导数值再乘以x的翻转值也就是y的值,而y的导数值同样等于z对t的导数值乘以x的值。
总结一下,在计算图中反向传播,加号导数值不变,乘号导数值乘以其翻转值。
5.2 计算图代码实践
这里,我们把要实现 的计算图的乘法节点称为“乘法层”(MulLayer),加法节点称为“加法层” (AddLayer)。我们来实践一个小例子如下
![]()
首先我们实现一个乘法类
class MulLayer:
def __init__(self): #初始化x和y,用于正向传播时保存值
self.x = None
self.y = None
def forward(self,x,y):#正向传播
self.x = x
self.y = y
out = x*y
return out
def backword(self,dout): #dout是导数值
dx = dout * self.y #反转x和y
dy = dout * self.x
return dx,dy
然后我们来买苹果
from layer_naive import MulLayer
apple = 100
apple_num = 2
tax = 1.1
#layer 层 一次乘法一个层
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
#forward
apple_price = mul_apple_layer.forward(apple,apple_num)
price = mul_tax_layer.forward(apple_price,tax)
print(100*2*1.1)
print(price)
#正确结果是220.0,不过如果出现220.00000000000003,浮点数表示小数的精度问题,可以忽略,或者用decimal模块。
同时我们在后面加上一段代码,反向传播
#backword
dprice = 1
dapple_price,dtax = mul_tax_layer.backword(dprice)
dapple,dapple_num = mul_apple_layer.backword(dapple_price)
print(dapple,dapple_num,dtax)
#结果2.2 110.0 200
#注意我们向前传播的参数顺序,和向后传播的参数顺序是相反的。
之后我们实现一个加法层
class AddLayer:
def __init__(self):#加法层反向传播导数值不变,不用存x和y
pass
def forward(self,x,y):
out = x + y
return out
def backwoard(self,dout):
dx = dout
dy = dout
return dx,dy
我们用代码实现一下买苹果和买橘子的过程。
from layer_naive import MulLayer,AddLayer
apple = 100
orange = 150
apple_num = 2
orange_num = 3
tax = 1.1
#层
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
#forward
apple_price = mul_apple_layer.forward(apple,apple_num)
orange_price = mul_orange_layer.forward(orange,orange_num)
apple_orange_price = add_apple_orange_layer.forward(apple_price,orange_price)
price = mul_tax_layer.forward(apple_orange_price,tax)
print(price)
#715.0000000000001
#backward
dprice = 1
dapple_orange_price,dtax = mul_tax_layer.backword(dprice)
dapple_price,dorange_price = add_apple_orange_layer.backwoard(dapple_orange_price)
dorange,dorange_num = mul_orange_layer.backword(dorange_price)
dapple,dapple_num = mul_apple_layer.backword(dapple_price)
print(dapple_num,dapple,dorange,dorange_num,dtax)
#110.00000000000001 2.2 3.3000000000000003 165.0 650
#关于浮点数表示小数的精度问题,我们忽略一下。
#综上可见,计算图中层的实现非常简单,使用这
#些层可以进行复杂的导数计算。下面,我们来实现神经网络中使用的层
5.3激活函数层的实现
5.3.1 ReLU层
现在,我们将计算图的思路应用到神经网络中。这里,我们把构成神经 网络的层实现为一个类。先来实现激活函数的ReLU层(以前用的sigmoid,这次我们用ReLU)和softmax层。
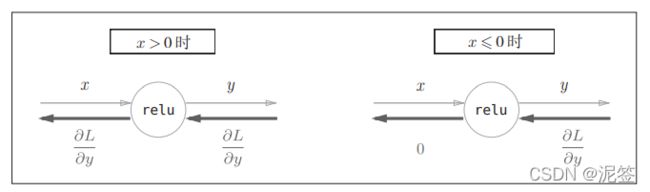
先看一下新的激活函数ReLu:大于0原样输出,小于等于0输出0

如果用计算图表示ReLu层就是下面的样子
用代码实现也非常简单
class Relu:
def __init__(self):
self.mask = None
def forward(self,x):
self.mask = (x<=0) #mask是与x同型的bool数组,元素大于0为false,小于等于0为true
out = x.copy()
out[self.mask] = 0 #大于0值不变,其他值变为0
return out
def backwoard(self,dout):
dout[self.mask] = 0 #小于等于0的变成0 常数的导数为0
dx = dout #大于0不变 x的导数为1,乘以1值不变
return dx
5.3.2 sigmoid层
计算图表示如下
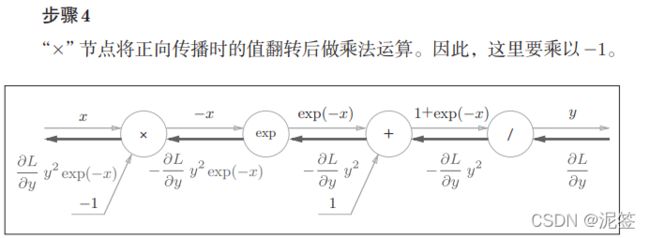
除了“×”和“+”节点外,还出现了新的“exp”和“/”节点。 “exp”节点会进行y = exp(x)的计算,“/”节点会进行y=1/x 的计算。
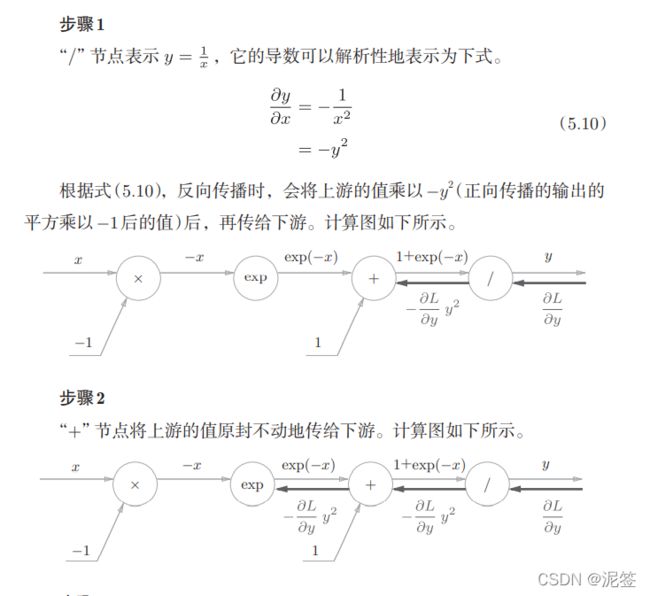
如何分析这个计算图的反向传播呢,我觉得没人能比书上说的更清楚了,直接截图如下:
步骤2的加法层我们很熟悉,除法层也很容易理解5.10的表达式,只不过有一点别扭它用y表示而不是用x,我们先接受这样的方式。
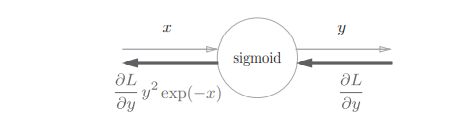
根据上述内容,计算图可以进行Sigmoid层的反向传播。而更简化的表达为如下计算图
我们整理下这个最终结果,将其中的x化简掉,变成一个y的表达式
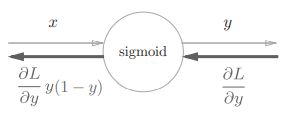
从而简化计算图,如下图所示的sigmoid层已经非常简单了
接下来我们用代码实现以下:
class Sigmoid:
def __init__(self):
self.out = None
def forward(self,x):
out = 1/(1+np.exp(-x)) #就是输出sigmoid(x)
self.out = out
return out
def backword(self,dout):
dx = dout*(1.0 - self.out)*self.out
# 不用numpy.dot 因为这里不是矩阵相乘,只是简单的乘法减法运算
return dx
5.4 简单矩阵求导
5.4.1 定义法求向量变元的导数
(书上没有这一段,我认为了解矩阵求导有帮助理解Affine层)
矩阵求导本质上只不过是多元函数求导,仅仅是把函数的自变量以及求导的结果排列成了矩阵的形式,方便表达与计算而已。
假设存在一个二元函数:f(x1,x2) = 2x1 + x2
我们很容易的算出函数对变量x1的偏导数为2,函数对变量x2的偏导数为1。
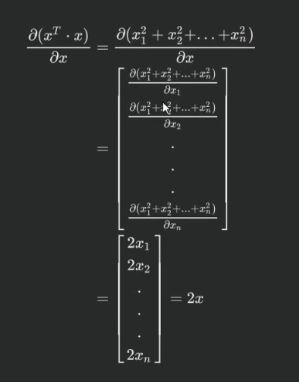
现在我们考虑将上述函数写为矩阵形式,我们把函数中的两个变量x1,x2一次排列组成一个向量变元,即一个由多个变量所组成的一个向量。如下
此时,如果我们按照向量变元内部的变量排列顺序,依次在每个变量位置填上该变量对应的偏导函数,则构成了对于函数f(x)进行向量变元X的求导的结果:
到此其实我们就完成了一次矩阵求导。
核心点在于,我们是依据向量变元中的变量排列顺序每一次填写了对应变量的偏导数函数计算结果。不够,更进一步的来看,既然方程组需要写成矩阵形式,那么原始函数的方程也可以写为:
结合求导结果我们发现,其实计算结果就是A。(结合矩阵与方程组的关系更容易理解)
至此,我们进行了一次矩阵求导的过程,之所以没有先给出定义,是觉得大家应该先对此有一个感觉,而不是用定义将大家的感觉框住。接下来给出详细的定义(注意x是向量变元不是矩阵):
大家觉得疑惑的一点是f函数怎么能对向量变元x求导,还得能对标量x1,x2…xn求偏导呢,其实我们要了解f函数只是一种映射关系。如果把f(x)写成f(x1,x2,…,xn)的形式,大家就会觉得容易接受了。其实f函数在这两种表达方式中是不变的。
5.4.2 熟悉了定义法求导后我们来推一些公式:(推公式的主要目的是熟悉定义法求导)
公式一:
公式二:
推导过程如下:(一步步看还是很简单的)
公式三:
推导:
公式四:
推导:只要把x的转置 A x都写成矩阵形式,然后按照定义发求导很容易就能推出,此处省略。
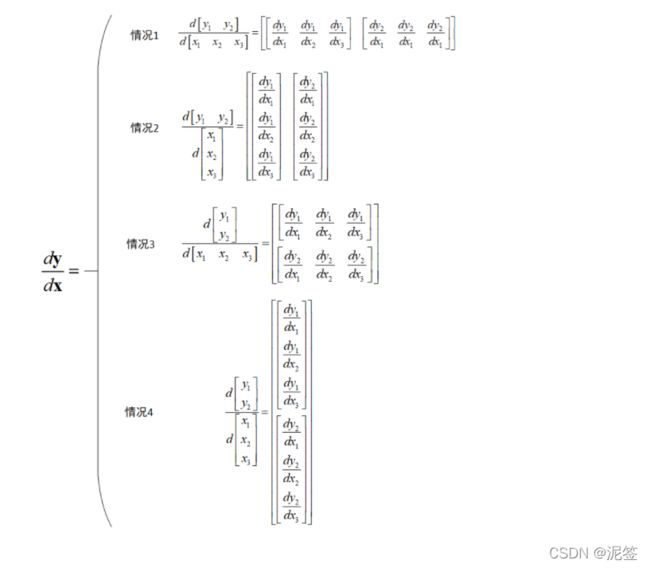
以上其实都转化为了每个变量元素对每个变量元素的求导,只不过形状我们可能有些不了解,下面来看一下向量向量求导的形状规则:
1)向量 y 的每个元素是标量,先做 y 的每个元素对向量 x 求导,这里按照标量对向量的求导规则进行。
2)第一步做好后,将求导结果按 y 的形状排列。
这是博客园一位无名者的图,向量对向量的求导我们解决了,矩阵对矩阵的求导完全可以变为向量对向量的求导,可以看一下这个链接矩阵求导
5.5 Affine 层的实现
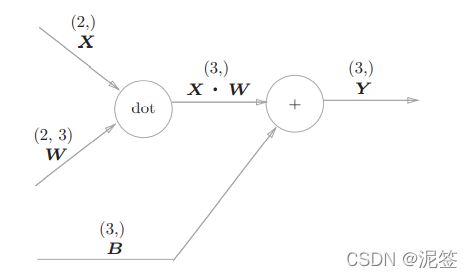
以前在神经网络的正向传播中使用了numpy.dot计算加权信号的值。神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿 射变换”。因此,这里将进行仿射变换的处理实现为“Affine层”。
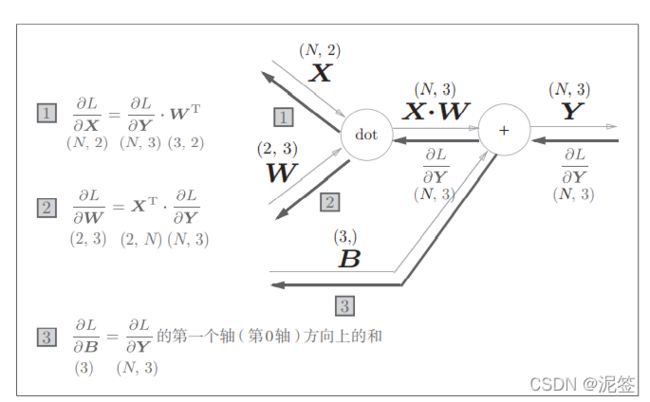
我们来尝试理解一下Affine层的计算图,注意此时的变量是矩阵
好吧,没有学过矩阵论,第二个找了很多资料还是没看懂怎么推出来的,让我先去系统的学习一下矩阵论,两个月之内回来更新,我们暂时接受结论就好。
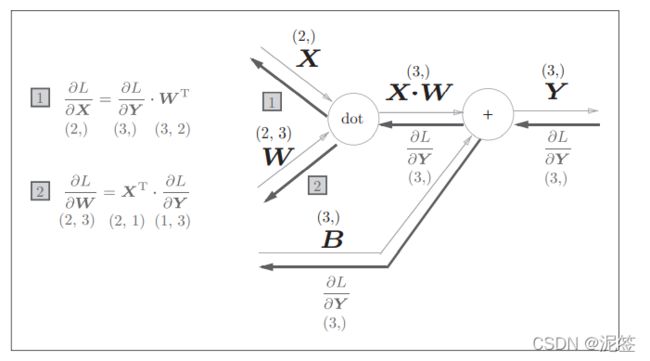
然后我们能得出计算图如下,
这里的X是单个数据,我们把它换成批处理的版本如下:
注意一点,偏置值B正向传播会被加到每一个数据上,所以反向传播时要将各个值汇总:
dB = np.sum(dY, axis=0)
然后就可以实现以下代码了:
class Affine:
def __init__(self,W,b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self,x):
self.x = x
out = np.dot(x,self.W) + self.b
return out
def backword(self,dout):
dx = np.dot(dout,self.W.T)
self.dW = np.dot(self.x.T,dout)
self.db = np.sum(dout,axis=0)
return dx
5.6 softmax-with-loss层计算图推导
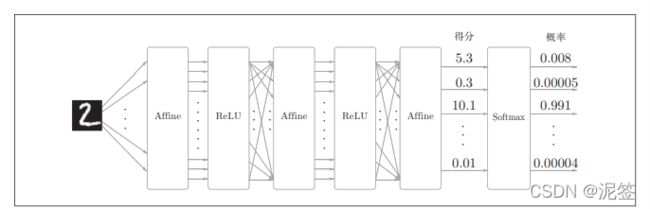
softmax函数会将输入值正规化之后再输出。比如手写数字识别时,Softmax层的输出如上图
神经网络中进行的处理有推理(inference)和学习两个阶段。神经网 络的推理通常不使用 Softmax层。比如,用上图的网络进行推理时, 会将最后一个 Affine层的输出作为识别结果。神经网络中未被正规 化的输出结果(上图Softmax层前面的 Affine层的输出)有时 被称为“得分”。也就是说,当神经网络的推理只需要给出一个答案 的情况下,因为此时只对得分最大值感兴趣,所以不需要 Softmax层。 不过,神经网络的学习阶段则需要 Softmax层。
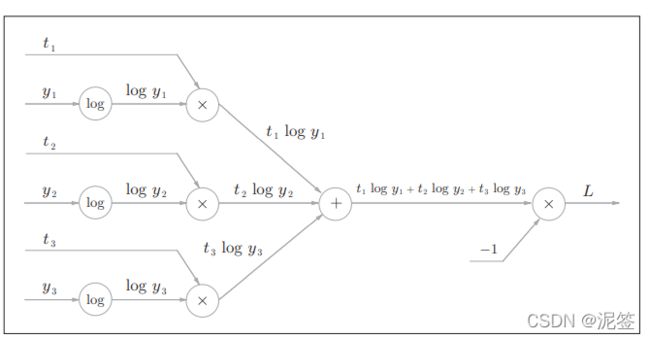
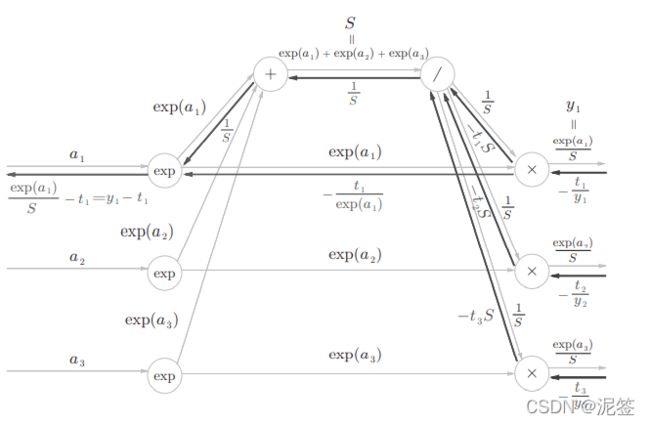
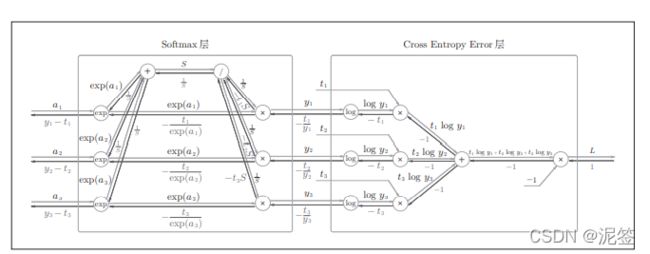
考虑到这里也包含作为损失函数的交叉熵误 差(cross entropy error),所以称为“Softmax-with-Loss层”。Softmax-with-Loss层(Softmax函数和交叉熵误差)的计算图如下图

这个计算图有些复杂,我们花些时间来推导一下
不想看推导过程的请直接跳过到softmax-with-loss层的实现,毕竟可能会损失掉一些兴趣。
开始推导:
5.6.1 正向传播
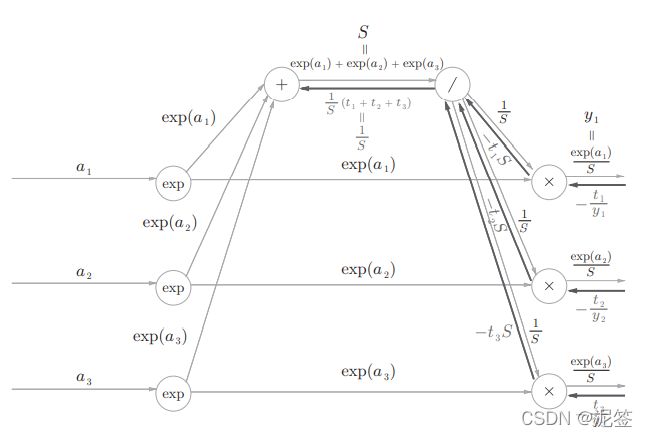
将分母这一部分和记为S,我们能得出计算图如下:
交叉熵误差我们也曾用代码实现过,
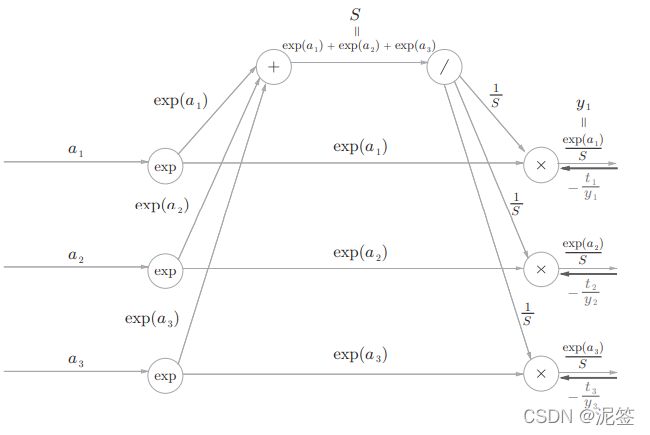
5.6.2反向传播
首先是Cross Entropy Error层的反向传播
这一层的反向传播还是很简单的,下面我们来看softmax层,我们一步一步来。
从loss传过来的数值我们卸载了乘号的右边。
步骤2:
这一步x节点将正向传播的值反转后相乘,如下式子:
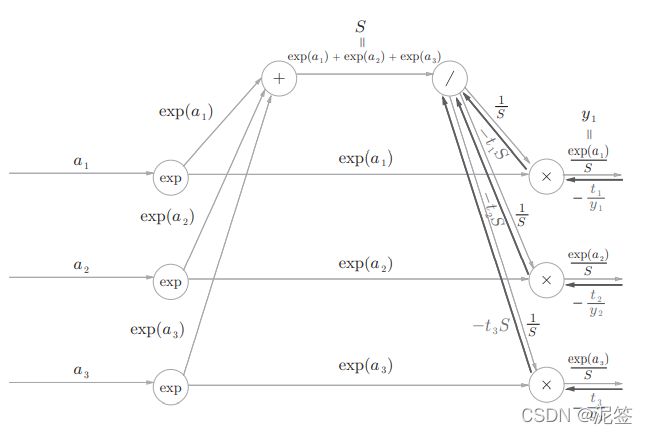
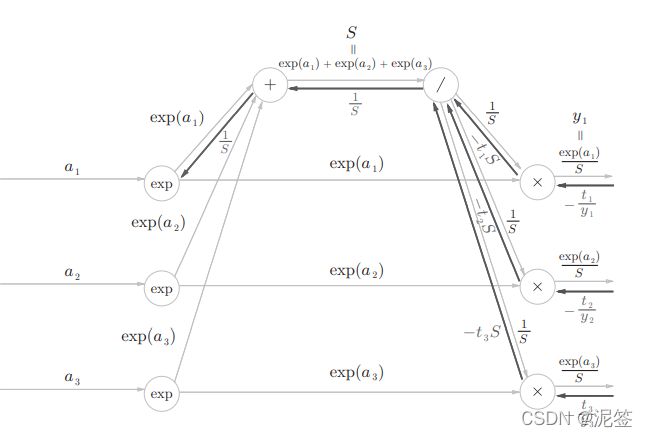
步骤3:
正如前面的Affine层的偏执值b一样,softmax层的除号节点将1/S的值传给下一层每一个节点。正向传播时三个分支流出反向传播时会被求和,1/S的导数很简单时-1/S**2,很容易得出结果(-1/S* * *2) * (-t1 * S - t2 * S -t3 * S)。由于此处的(t1,t2,t3)是教师标签也就是one-hot数组,所以ti的和是1,所以得出结果(1/S)。
加号 原封不动传递值。
步骤5:
这里求的是乘号节点的另一个反向分支,很容易的除结果。
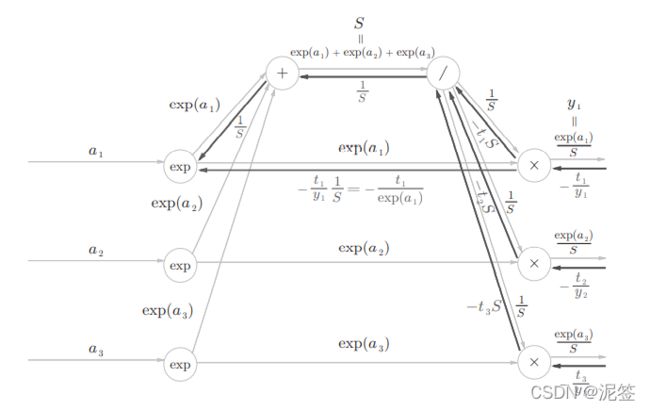
步骤6:
exp号我们处理过,不过这个地方注意有两个分支,所以举个例子,i=1时结果是(1/S-t1/exp(a1))exp(a1)。
exp(x)的导数是exp(x),注意此处x是a1。整理一下就是y1-t1。
由此,我们推导完了softmax层,接下来我们把他俩合在一起。
softmax-with-loss层
这个计算图看似复杂,但是一步步走下去也没有很难。确定的是,计算图比去看误差反向传播的数学公式推导简单的多的多的多。
5.7 softmax-with-loss层的实现
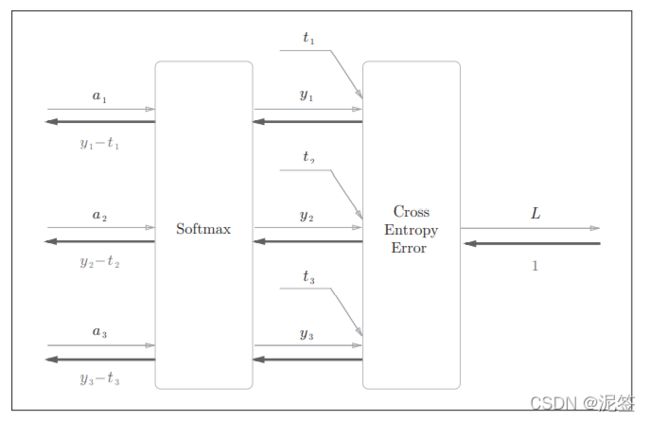
经过推导我们可以把softmax层和cross-entropy-error层的内部细节隐藏变成如下所示的简洁版softmax-with-loss层计算图。
注意softmax反向传播的结果是(y1-t1,y2-t2,y3-t3)。而(y1,y2,y3)恰好是softmax层的输出,(t1,t2,t3)是监督数据,所以(y1-t1,y2-t2,y3-t3)是softmax层的输出和教师标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层,这是神经网络学习的重要性质。
这里考虑一个具体的例子,比如思考教师标签是(0, 1, 0),Softmax层 的输出是(0.3, 0.2, 0.5)的情形。因为正确解标签处的概率是0.2(20%),这个 时候的神经网络未能进行正确的识别。此时,Softmax层的反向传播传递的 是(0.3, −0.8, 0.5)这样一个大的误差。因为这个大的误差会向前面的层传播, 所以Softmax层前面的层会从这个大的误差中学习到“大”的内容。
使用交叉熵误差作为 softmax函数的损失函数后,反向传播得到 (y1 − t1, y2 − t2, y3 − t3)这样“漂亮”的结果。实际上,这样“漂亮” 的结果并不是偶然的,而是为了得到这样的结果,特意设计了交叉 熵误差函数。回归问题中输出层使用“恒等函数”,损失函数使用 “平方和误差”,也是出于同样的理由(3.5节)。也就是说,使用“平 方和误差”作为“恒等函数”的损失函数,反向传播才能得到(y1 − t1, y2 − t2, y3 − t3)这样“漂亮”的结果。
现在我们来用代码实现一下softmax-with-loss层。
我们之前的章节实现了softmax函数和损失函数cross_entropy_error函数。
class SoftMaxTithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self,x,t):
self.t = t
self.y = softmax(x)
self.loss =cross_entropy_error(self.y,self.t)
return self.loss
def backward(self,dout = 1):
batch_size = self.t.shape[0]
dx = (self.y - self.t)/batch_size #一次mini_batch的平均损失函数
return dx
至此,我们完成了误差反向传播算法所需要的层。
5.8 误差反向传播算法的实现
我们把前面实现的所有层的类写到一个py文件
from deeplearning.fuction import softmax,cross_entropy_error
import numpy as np
class Relu:
def __init__(self):
self.mask = None
def forward(self,x):
self.mask = (x<=0) #mask是与x同型的bool数组,元素大于0为false,小于等于0为true
out = x.copy()
out[self.mask] = 0 #大于0值不变,其他值变为0
return out
def backward(self,dout):
dout[self.mask] = 0 #小于等于0的变成0 常数的导数为0
dx = dout #大于0不变 x的导数为1,乘以1值不变
return dx
class Sigmoid:
def __init__(self):
self.out = None
def forward(self,x):
out = 1/(1+np.exp(-x)) #就是输出sigmoid(x)
self.out = out
return out
def backword(self,dout):
dx = dout*(1.0 - self.out)*self.out
# 不用numpy.dot 因为这里不是矩阵相乘,只是简单的乘法减法运算
return dx
class Affine:
def __init__(self,W,b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self,x):
self.x = x
out = np.dot(self.x,self.W) + self.b
return out
def backward(self,dout):
dx = np.dot(dout,self.W.T)
self.dW = np.dot(self.x.T,dout)
self.db = np.sum(dout,axis=0)
return dx
class SoftMaxTithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self,x,t):
self.t = t
self.y = softmax(x)
self.loss =cross_entropy_error(self.y,self.t)
return self.loss
def backward(self,dout = 1):
batch_size = self.t.shape[0]
dx = (self.y - self.t)/batch_size #一次mini_batch的平均损失函数
return dx
#然后搭建神经网络
import numpy as np
from collections import OrderedDict
from net_layer import *
from deeplearning.fuction import numerical_gradient
class TwoLayerNet:
def __init__(self,input_size,hidden_size,output_size,
weight_init_std=0.01):
#初始化权重
self.params = {}
self.params['W1'] = weight_init_std*np.random.randn(input_size,hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std*np.random.randn(hidden_size,output_size)
self.params['b2'] = np.zeros(output_size)
"""
OrderedDict是有序字典
"""
#生成层
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'],self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'],self.params['b2'])
self.lastLayer = SoftMaxTithLoss()
#有序字典的作用 体现在向前传播
def predict(self,x):
for layer in self.layers.values():
x = layer.forward(x)
return x
#损失函数 我们以前得到的y是softmax之后的,现在的predict并没有经过softmax
def loss(self,x,t):
y = self.predict(x)
return self.lastLayer.forward(y,t)
def accuracy(self,x,t):
y = self.predict(x) #y获得得分情况
y = np.argmax(y,axis = 1) #没经过softmax y获得最高得分
if t.ndim != 1 : #如果t是1维 axis=1会出错,mini_batch不会是1维
t = np.argmax(t,axis = 1)
acuracy = np.sum((y==t)/float(x.shape[0]))
return acuracy
#数值微分法求梯度
def numerical_gradient(self,x,t):
loss_W = lambda W:self.loss(x,t)
grads = {}
grads['W1'] = numerical_gradient(loss_W,self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
#误差反向传播求梯度
def gradient(self,x,t):
#forward 向前传播就是获取损失函数值的过程
self.loss(x,t)
#backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads
5.8.2 梯度确认
数值微分相比于误差反向传播慢太多了,但是公式简单,准确性高,所以我们仍保留了数值微分法对误差反向传播法所求的梯度进行梯度确认。
我们来实现以下梯度确认的代码,注意会用到读出mnist数据集的代码,不在本文的范畴内,我会将所有源码放在本文的最后,大家直接用就行了。
import numpy as np
from deeplearning.mnist import load_mnist
from bp_two_layer_net import TwoLayerNet
(x_train,t_train),(x_test,t_test) = load_mnist(normalize=True,
one_hot_label=True)
network = TwoLayerNet(input_size=784,hidden_size=50,output_size=10)
x_batch = x_train[:3]
t_batch = t_train[:3]
print(t_batch)
print(x_batch.shape)
# 计算梯度
grad_numerical = network.numerical_gradient(x_batch,t_batch)
grad_backprop = network.gradient(x_batch,t_batch)
for key in grad_numerical.keys():
diff = np.average(np.abs(grad_backprop[key]-grad_numerical[key]))
print(key+":"+str(diff))
"""
W1:5.149479600079807e-10
b1:3.1285116192493813e-09
W2:6.50174656746636e-09
b2:1.4024284498564966e-07
差值非常小 可以忽略不计
"""
最后让我们训练这个二层bp人工神经网络
from bp_two_layer_net import TwoLayerNet
import numpy as np
from deeplearning.mnist import load_mnist
import matplotlib.pyplot as plt
(x_train,t_train),(x_test,t_test) = load_mnist(normalize=True,one_hot_label=True)
network = TwoLayerNet(input_size=784,hidden_size=50,output_size=10)
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size/batch_size,1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size,batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
#反向误差获取梯度
grad = network.gradient(x_batch,t_batch)
#更新梯度
for key in ('W1','b1','W2','b2'):
network.params[key] -= learning_rate*grad[key]
loss = network.loss(x_batch,t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train,t_train)
test_acc = network.accuracy(x_test,t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc,test_acc)
print("训练结束,开始画图:")
f1 = plt.figure()
x = np.arange(len(train_loss_list))
y = np.array(train_loss_list)
plt.xlabel("mini_batch")
plt.ylabel("loss")
plt.plot(x,y)
f2 = plt.figure()
x2 = np.arange(len(train_acc_list))
y1 = np.array(train_acc_list)
y2 = np.array(test_acc_list)
plt.xlabel("mini_batch")
plt.ylabel("accuracy")
plt.plot(x2,y1,label="train data")
plt.plot(x2,y2,linestyle="--",label="test data")
plt.legend()
plt.show()
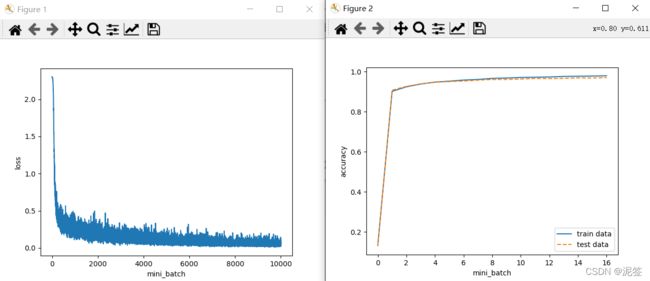
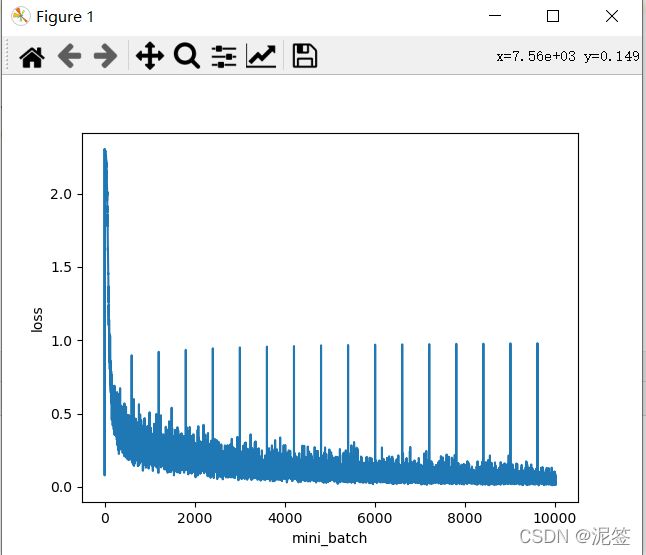
两个图像如下
一张是损失函数值关于mini_batch训练次数的图像,肉眼可见逐步收敛接近0。第二张是训练数据正确率和测试数据正确率,可见泛化程度很好,没有过拟合。
打印结果也贴出来:
0.1328666666666667 0.1284
0.9012833333333337 0.9073000000000002
0.9240833333333335 0.9263000000000002
0.9380500000000003 0.9390000000000003
0.9476333333333338 0.9470000000000003
0.9523000000000003 0.9503000000000003
0.9579000000000002 0.9531000000000003
0.9609000000000002 0.9573000000000003
0.9661833333333335 0.9608000000000003
0.9680333333333335 0.9609000000000003
0.9708166666666669 0.9631000000000004
0.9719833333333336 0.9658000000000002
0.9733666666666668 0.9653000000000004
0.9758666666666669 0.9664000000000004
0.9769000000000002 0.9686000000000003
0.9778833333333334 0.9681000000000004
0.9792000000000004 0.9701000000000004
训练结束,开始画图:
Process finished with exit code 0
误差反向传播法至此结束了,写了好多,矩阵求导那一块暂时拖欠了,过两个月后来还,另外给大家看一个bug
大家可以思考下为什么会出现这种状况。
因为我把正确率加到损失函数值上了!




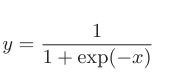


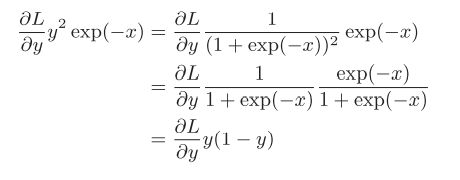
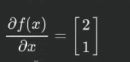

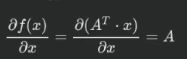


![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bAYF8NQ0-1644493498444)(五、误差反向传播法.assets/图5-24-1644286354792.png)]](http://img.e-com-net.com/image/info8/c07c283a6282487c98a564863bbb24f1.jpg)

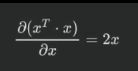
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vlFoHJZ2-1644493498446)(五、误差反向传播法.assets/图5-28.png)]](http://img.e-com-net.com/image/info8/9479deaa3f5f470a87d90dd88f2ac513.jpg)