数据结构与算法——第三节 链表(单向不循环不带头+双向循环带头 C实现+源码剖析+运行+思路分析)
大家好,我是@jxwd,
开心学编程,学到无极限。
你还在数据结构的苦海中挣扎吗?
你难道还在抱着一本厚厚的数据结构书在那里硬啃吗?
你难道还是对于数据结构一无所措吗?
别急,因为~~~
在未来的几个月里,我会为大家推出精品的数据结构文章。涵盖广、内容深。
如果你能够静下心来,看了我的文章以后,你会发现,课本就是一本小说。
我在未来还会给大家推出视频,用视频的方式讲解。
想要了解我的视频,以及我的文章,那就持续关注我,订阅专栏《完全自学数据结构与算法和C++》吧
本节的内容为 链表 !
目录
链表的存在意义和背景
链表的构成与定义
链表的分类
双链表的实现
函数1:打印链表 void ListPrint(ListNode* phead);
函数2:ListNode* BuyListNode(LTDataTYpe x);//创建新节点
函数3:ListNode* ListInit();//初始化链表
函数4:void ListNodePushFront(ListNode* phead, LTDataTYpe x);//头插
函数5:void ListNodePushBack(ListNode* phead, LTDataTYpe x);//尾插
函数6:void ListPopFront(ListNode* phead);//头删
函数7:void ListPopBack(ListNode* phead);//尾删
函数8:ListNode* ListFind(ListNode* phead, LTDataTYpe x); //寻找数据域为x的节点,返回该节点
函数9:void ListInsert(ListNode* pos, LTDataTYpe x);//在pos节点的后面插入一个元素
函数10:void ListErase(ListNode* pos);//删除pos节点
函数11:int ListEmpty(ListNode* phead);//判断链表是否为空
函数12:int ListSize(ListNode* phead);//判断链表的大小(头节点是不算的)
函数13:void ListDestory(ListNode* phead);//销毁链表
单链表的实现
函数1:void SListPrint(SListNode* plist); //打印链表
函数2:SListNode* BuySListNode(SLTDataType x); //创建新节点
函数3:void SListPushBack(SListNode** pplist, SLTDataType x);//尾插
函数4:SListNode* SListPushFront(SListNode** pplist, SLTDataType x);//头插
函数5:void SListPopBack(SListNode** pplist); //尾删
函数6:void SListPopFront(SListNode** pplist); //头删
函数7:SListNode* SListFind(SListNode* plist, SLTDataType x); //寻找节点
函数8:void SListInsertAfter(SListNode* pos, SLTDataType x); //在目标节点的后面插入
函数9:void SListInsertBefore(SListNode** pplist, SListNode* pos, SLTDataType x);//在目标节点的前面插入
函数10:void SListEraseAfter(SListNode* pos); //删除pos节点的下一个节点
函数11:void SListEraseCur(SListNode** pplist, SListNode* pos); //删除pos节点
函数12:void SListDestory(SListNode** plist);//销毁链表
链表和顺序表的对比:
链表的存在意义和背景
链表,又叫线性表的链式存储结构。
我们在前面曾经说过线性表;而线性表有其缺点,其缺点就是对于数据的增加和删除极为麻烦;
一个元素如果要增加或者删除,那么整个后面的元素都要移动。
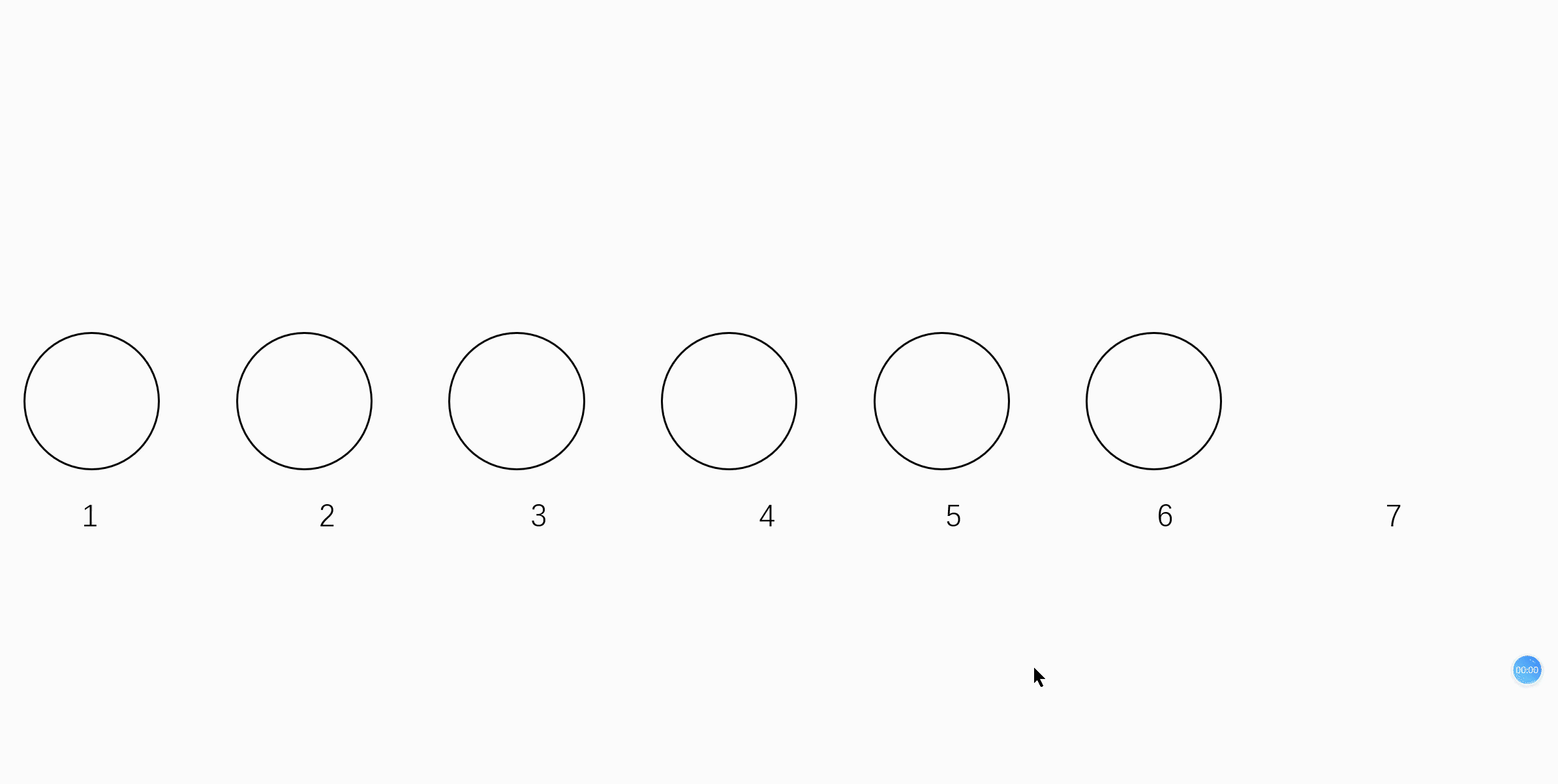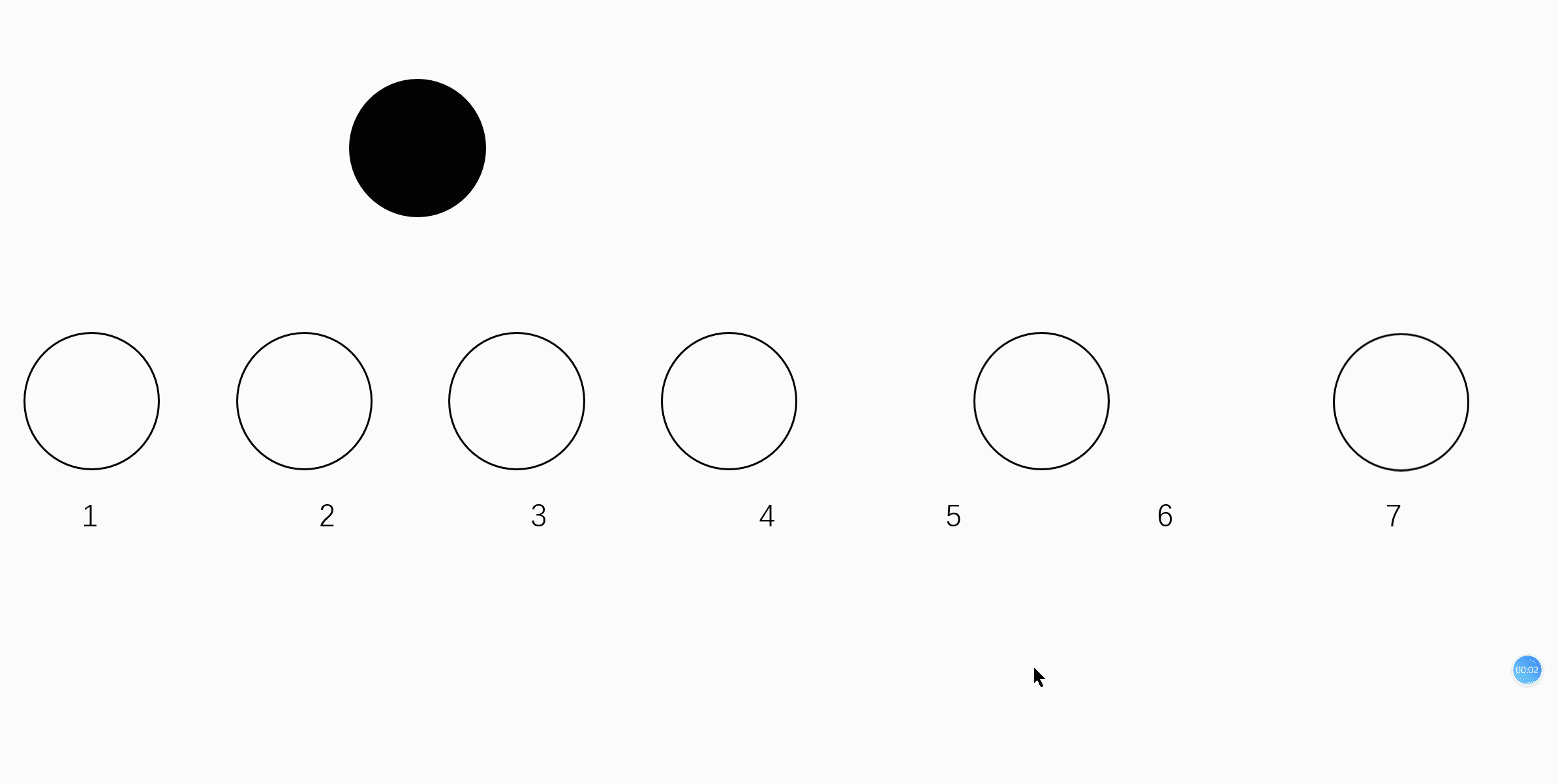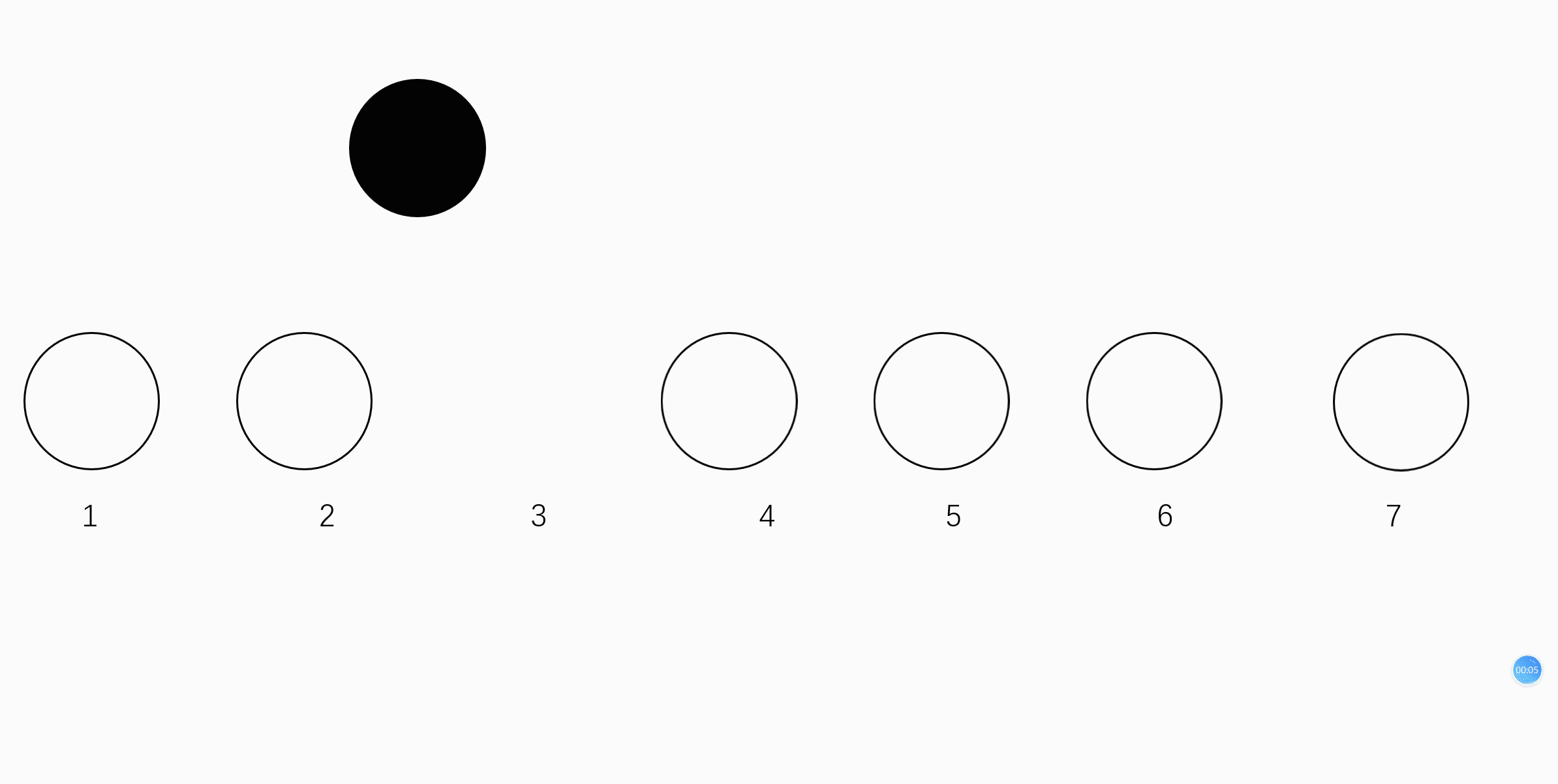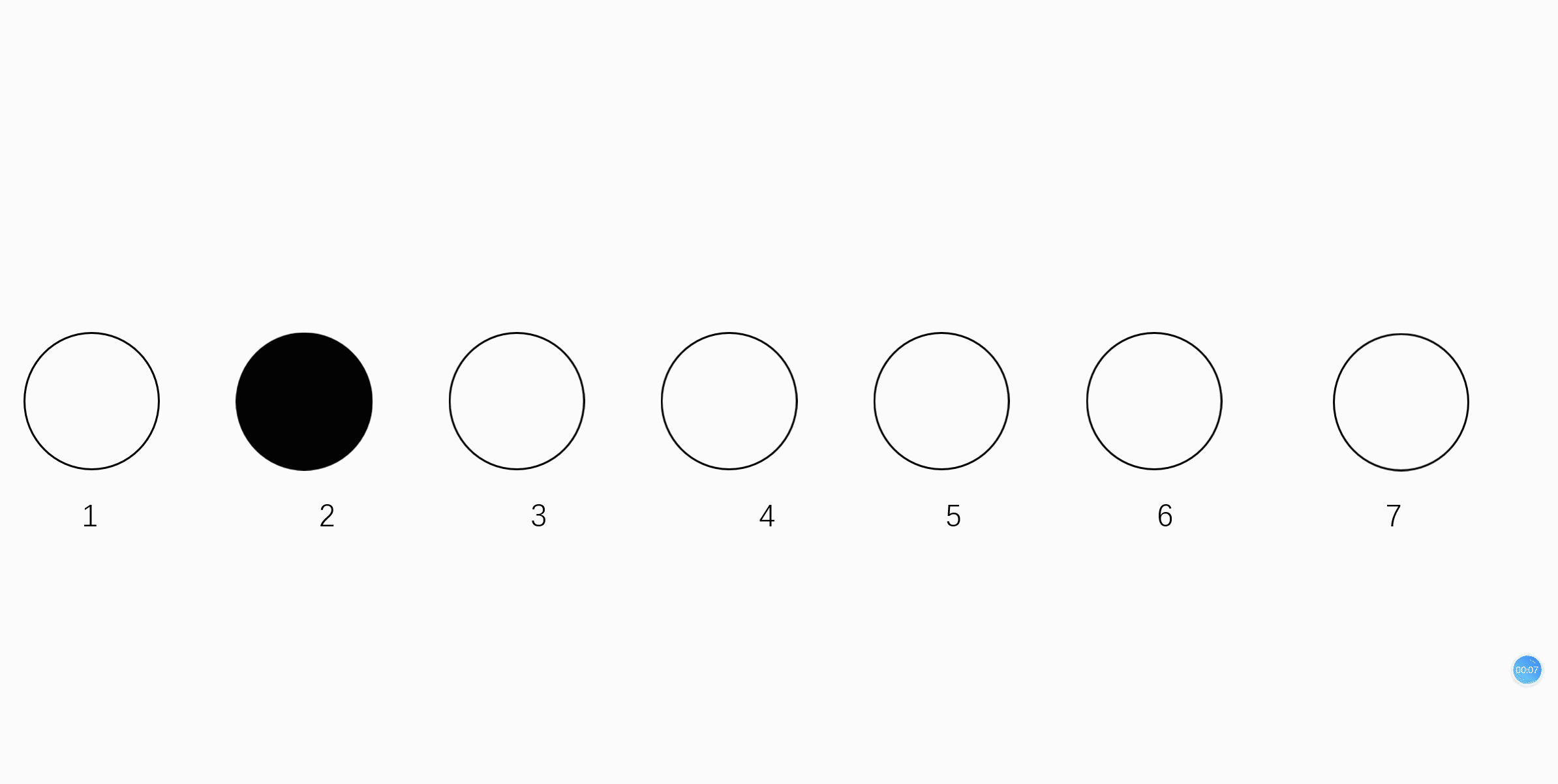
如下图:
可以看到 ,我如果要吧黑球插入到白球里面,显然,我要把7号位的球移到8号位,5号位的球移到6号位...然后最后才能把2号位的求插进去。如果有N个数据,那么它的算法的时间复杂度达到了O(N)!
那有没有什么好的方法来解决这种问题呢?
当然是有的——链表就出现了。
链表的构成与定义
对于一个链表来说,和顺序表一样,我们认为其也需要节点,也是由一个个节点构成的。
在这样的一个节点中,我们需要存储一些数据,从而能够使得所有的节点连接起来形成一个链表。
在以前的顺序结构存储中,每个元素只需要存储元素信息就可以了。而对于链表而言,它不仅仅需要存储元素的信息,还要存储一个能够表示前后节点的关系的东西,这个东西我们用指针来实现。
所以总结来说,一个节点最少需要存储两样东西:数据信息和(下一个节点的)指针。
于是n个这样的节点就构成了一个链表,即线性表的链式存储结构。
这样,我们也就可以用一个结构体来表示节点中的内容了:
(同样的,还是将int 类型重新命名)
typedef int SLTDataType;
typedef struct SListNode
{
SLTDataType data;
SListNode* next;
}SListNode;这是最简单的节点的构成。
链表的分类
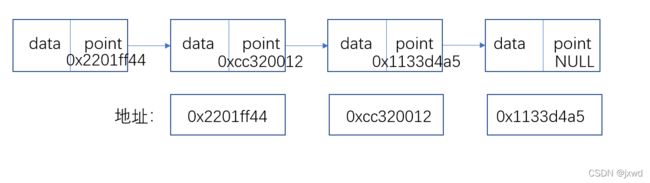
对于链表而言,我们有单向不循环的链表:就是像刚刚所写的节点那样。
这样的节点之间的关系可以表示为:
(第一个节点的地址我没有写;最后一个节点的指针指向的为空)
(该图为单向不循环无头节点)
但是,上述的节点只是能够访问下一个节点的内容。(因为其指针是指向下一个节点)
有的时候,我如果想要访问上一个节点怎么办呢?
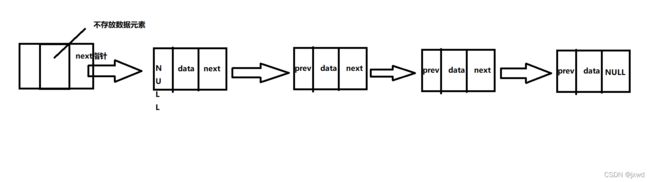
于是乎,我们就又出现了双向链表;即在一个链表当中,既存在一个指针指向下一个节点,又存在一个指针指向上一个节点。
(双向不循环无头结点)
如果我们想让连表有一个头呢?
这样我们在调用的时候想改变链表,我们就直接可以传头指针就可以了,否则还需要传二级指针,非常麻烦。
于是乎,又出现了一种新的链表:
双向带头不循环:
那有没有这样一种办法:
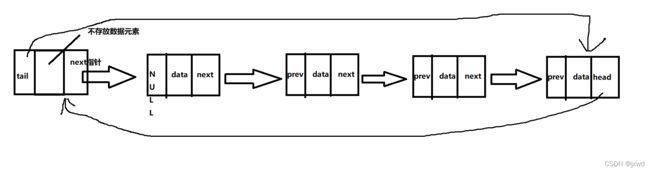
我通过末尾的节点就能够直接找到头节点呢?
我把最后一个节点的next指针利用起来,让其指向头指针,并且同时把头节点的prev指针利用起来,让它指向末尾的节点,可以吗?
答案是肯定的。
这样的话,我们就构成了一种新的链表类型——双向带头循环链表
所以我们可以来做一下总结:
不带头 单向 不循环
带头 双向 循环
这样的话,总共有2*2*2=8种不同的链表类型。
而我们今天,主要来讲 不带头单向不循环链表 和 带头双向循环链表
一种 是最简单的,还有一种是最复杂的。
掌握了这两种写法呢,其他的就基本上拼拼凑凑,就出来了。
(我们上面所画出来的结构,叫逻辑结构;链表实际在内存中存储的方式叫做物理结构)
话不多说,我们开始实现:
由于笔者觉得双链表在实现起来比单链表简单(在代码的实现上),故笔者决定先说双链表,再说单链表。
注:本文所说的单链表指的都是单向不带头不循环链表;
所说的双链表指的都是带头双向循环链表。
双链表的实现
我们这里的双链表,指的就是双向带头循环链表
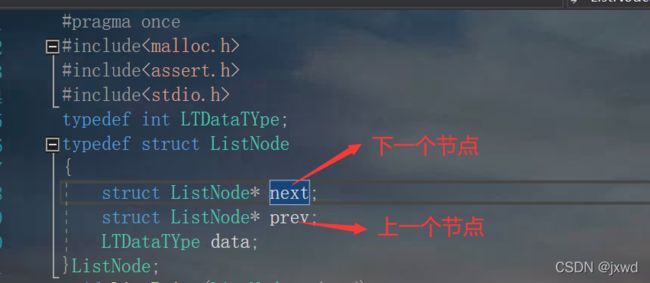
我们同样,定义一个节点:
如上图,next是指向下一个节点的指针;
prev是指向下一个节点的指针。
#pragma once
#include
#include
#include
typedef int LTDataTYpe;
typedef struct ListNode
{
struct ListNode* next;
struct ListNode* prev;
LTDataTYpe data;
}ListNode;
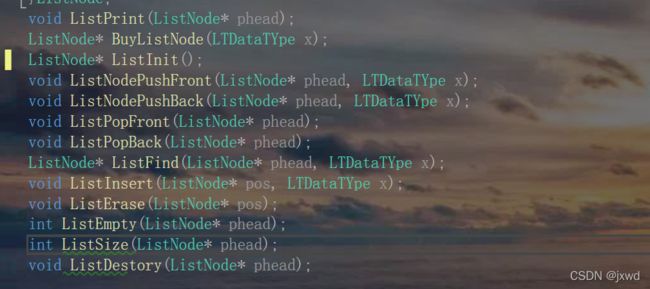
我们接下来要依次实现下列函数
void ListPrint(ListNode* phead); //函数1:打印链表
ListNode* BuyListNode(LTDataTYpe x);//函数2:创建新节点
ListNode* ListInit(); //函数3:初始化链表
void ListNodePushFront(ListNode* phead, LTDataTYpe x);//函数4:头插
void ListNodePushBack(ListNode* phead, LTDataTYpe x);//函数5:尾插
void ListPopFront(ListNode* phead); //函数6:头删
void ListPopBack(ListNode* phead); //函数7:尾删
ListNode* ListFind(ListNode* phead, LTDataTYpe x); //函数8:寻找节点
void ListInsert(ListNode* pos, LTDataTYpe x); //函数9:在pos的后面插入节点
void ListErase(ListNode* pos); //函数10:删除pos节点
int ListEmpty(ListNode* phead); //函数11:判断链表是否为空
int ListSize(ListNode* phead); //函数12:求链表的大小
void ListDestory(ListNode* phead); //函数13:销毁链表我们一网打尽,和顺序表一样的方式来介绍:
函数1:打印链表 void ListPrint(ListNode* phead);
这个就是送分题,非常的简单。我们麻溜点,直接上代码了。
void ListPrint(ListNode* phead)
{
ListNode* cur = phead->next;
while (cur != phead) //循环遍历,逐个打印
{
printf("%d", cur->data);
if (cur->next != phead)
{
printf("->");
}
cur = cur->next;
}
printf("\n");
}在这里,想请读者注意一下:
由于这里我们是双向循环链表,就是说,最后一个节点的next所存放的地址不再为空指针;而是头节点的地址。
所以我们这里的判断条件都是cur->next != phead,或者cur != phead(因为其转了一圈回来又回到头指针上面去了)
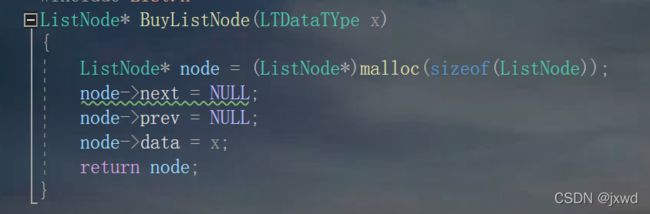
函数2:ListNode* BuyListNode(LTDataTYpe x);//创建新节点
该函数和我们在单链表中的实现方式本质上一样。
ListNode* BuyListNode(LTDataTYpe x)
{
ListNode* node = (ListNode*)malloc(sizeof(ListNode));
//动态开辟一块空间
node->next = NULL;
node->prev = NULL;//两个指针都先置空
node->data = x; //数据域放进去
return node; //返回新创建的该指针
}函数3:ListNode* ListInit();//初始化链表
该函数的主要作用是创建头节点;从而达到初始化链表的目的。
ListNode* ListInit()
{
ListNode* phead = BuyListNode(0);
//创建一个节点,作为头节点。数据域可以随便赋值
phead->next = phead;
phead->prev = phead;//头节点的next和prev指针都指向phead
return phead; //返回该头节点
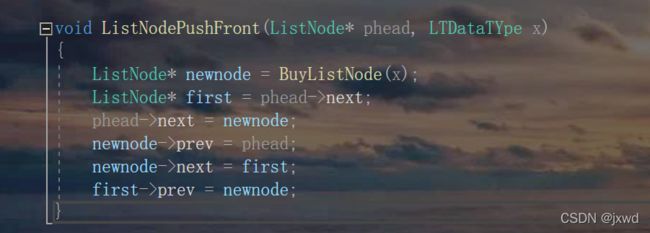
}函数4:void ListNodePushFront(ListNode* phead, LTDataTYpe x);//头插
void ListNodePushFront(ListNode* phead, LTDataTYpe x)
{ //注意该头插指的是插到头节点的后面
ListNode* newnode = BuyListNode(x);//创建新节点
ListNode* first = phead->next; //第一个节点(非头节点记为first节点)
phead->next = newnode;
newnode->prev = phead;
newnode->next = first;
first->prev = newnode; //三节点交换指针指向关系
}三节点交换指针指向关系可以用下面的动图 来演示:
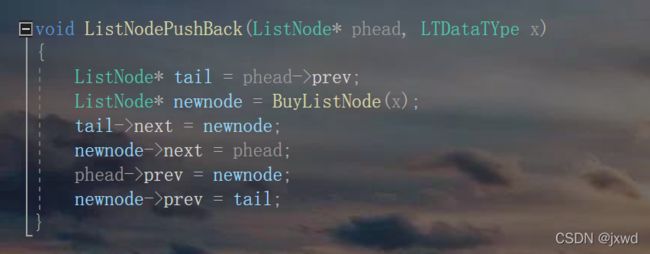
函数5:void ListNodePushBack(ListNode* phead, LTDataTYpe x);//尾插
这里就相当于插入到了头节点的前面
原理和头插一模一样,不再赘述
void ListNodePushBack(ListNode* phead, LTDataTYpe x)
{
ListNode* tail = phead->prev;
ListNode* newnode = BuyListNode(x);
tail->next = newnode;
newnode->next = phead;
phead->prev = newnode;
newnode->prev = tail;
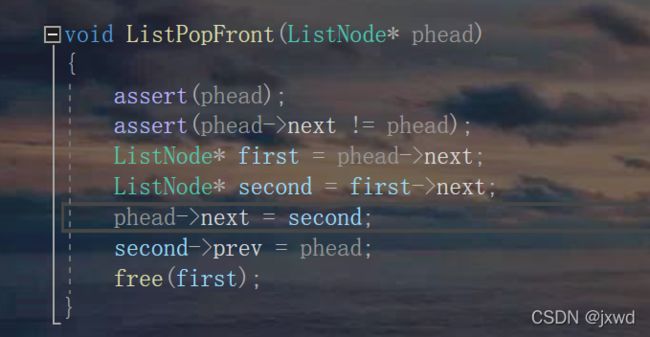
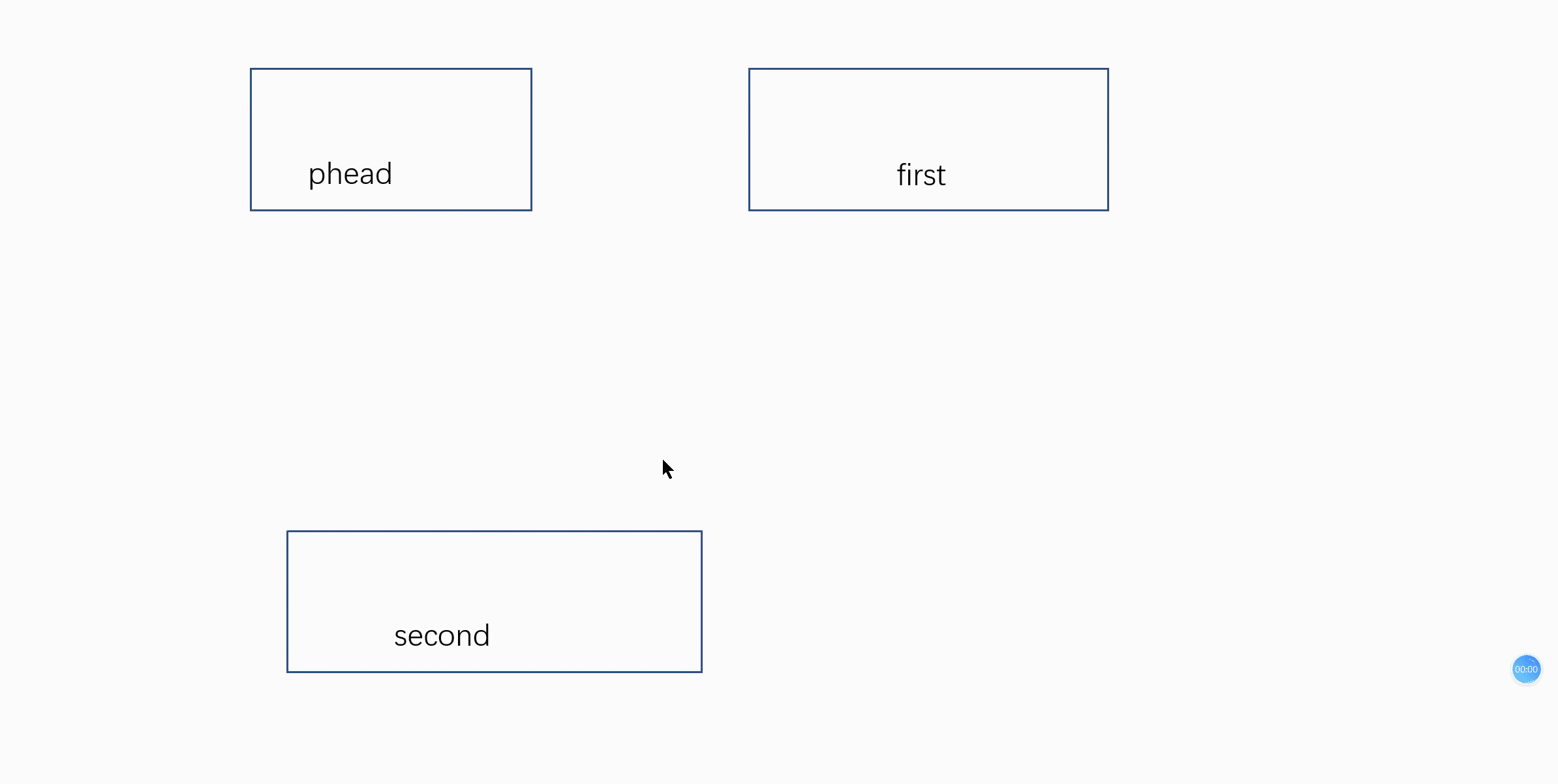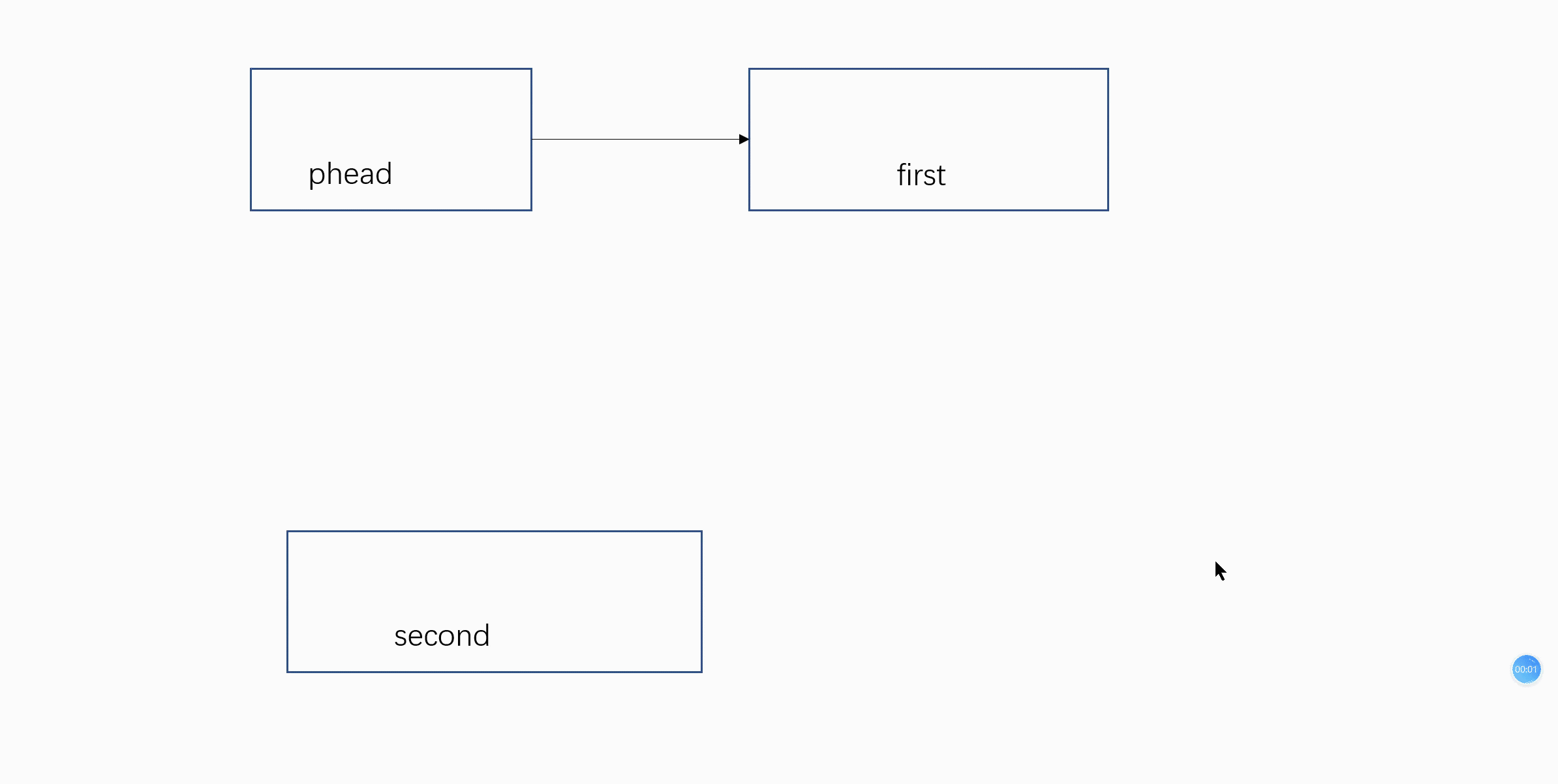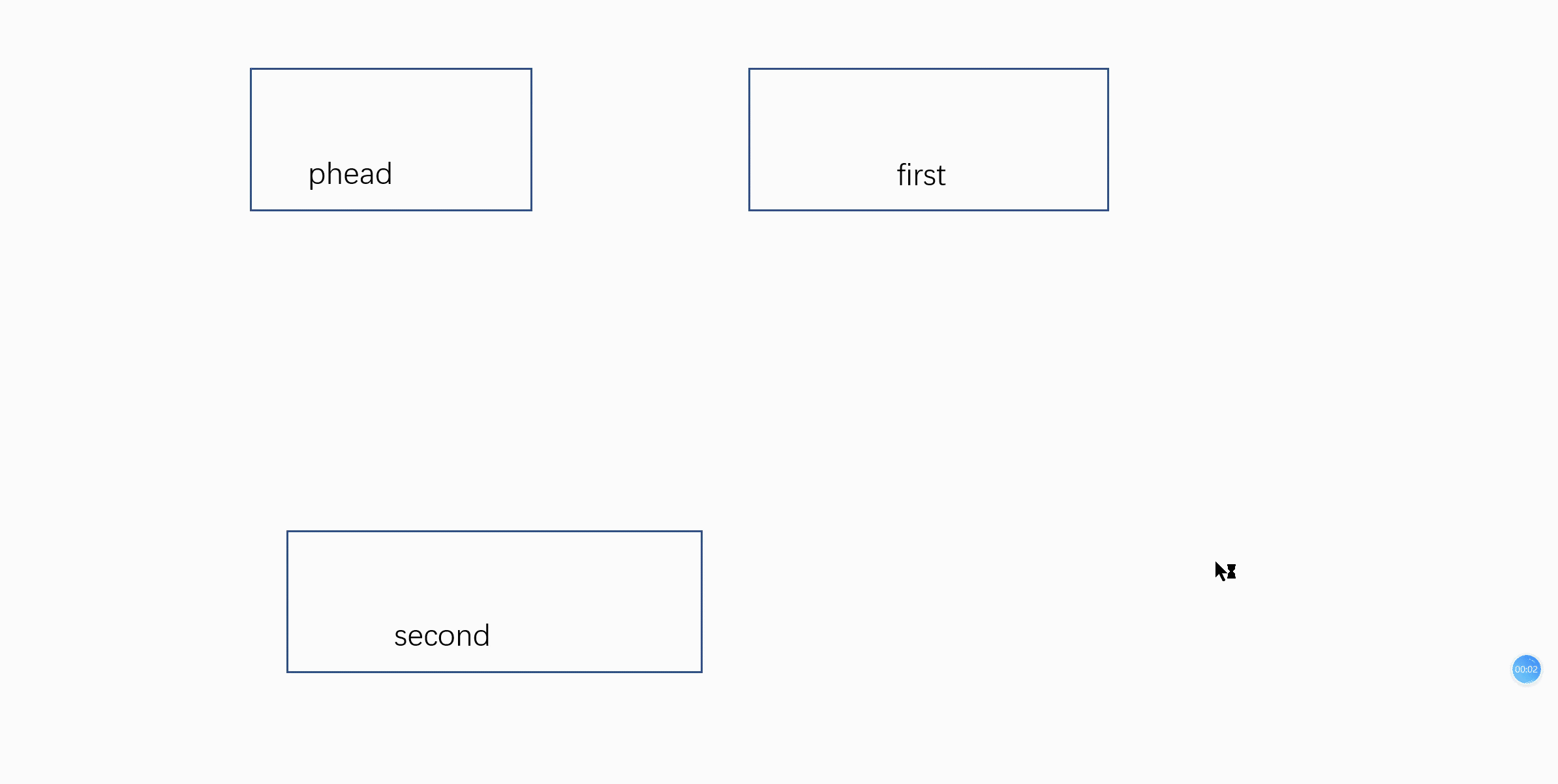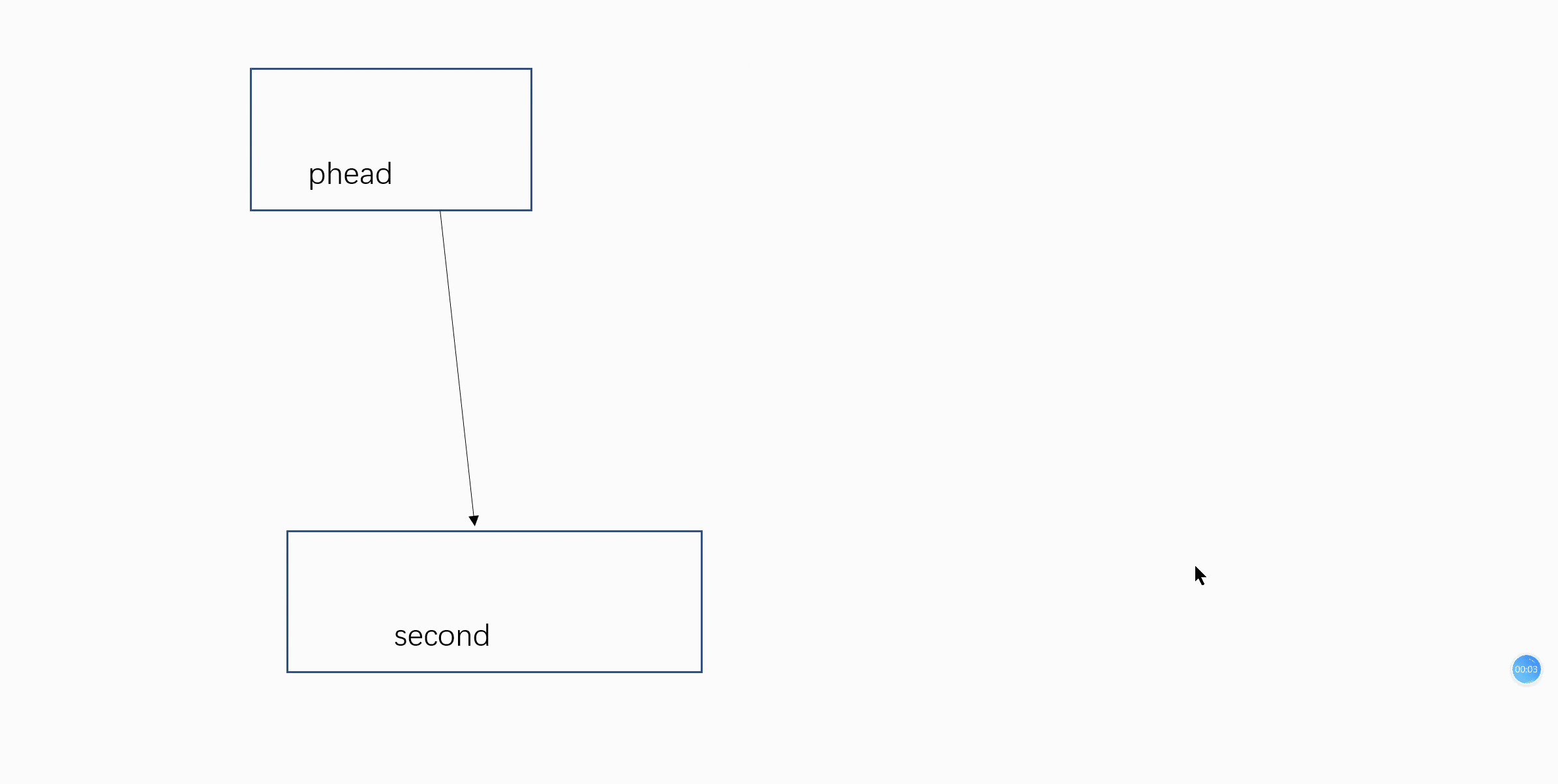
}函数6:void ListPopFront(ListNode* phead);//头删
就是把头节点后面的节点删除
void ListPopFront(ListNode* phead)
{
assert(phead);
assert(phead->next != phead); //两步断言一下
ListNode* first = phead->next;
ListNode* second = first->next;
phead->next = second;
second->prev = phead; //同样的道理,三指针交换
free(first); //注意要free
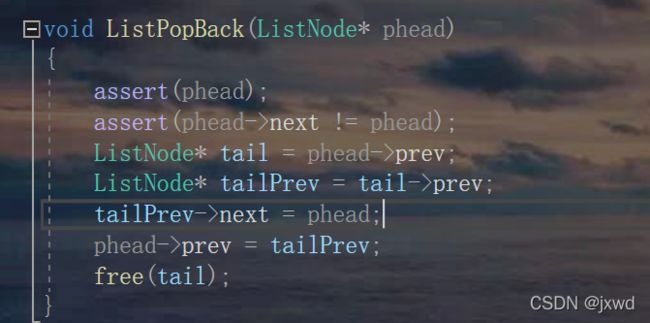
}函数7:void ListPopBack(ListNode* phead);//尾删
同理即可,就是相当于删除头节点前面的那个节点
不再赘述
void ListPopBack(ListNode* phead)
{
assert(phead);
assert(phead->next != phead);
ListNode* tail = phead->prev;
ListNode* tailPrev = tail->prev;
tailPrev->next = phead;
phead->prev = tailPrev;
free(tail);
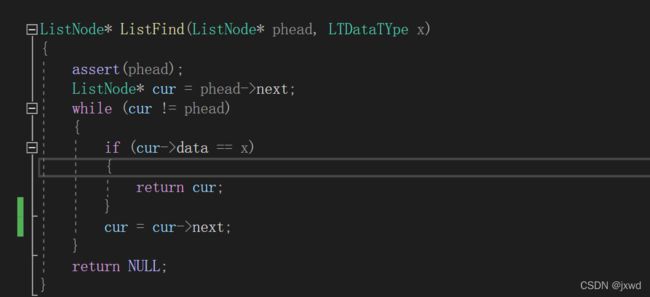
}函数8:ListNode* ListFind(ListNode* phead, LTDataTYpe x); //寻找数据域为x的节点,返回该节点
ListNode* ListFind(ListNode* phead, LTDataTYpe x)
{
assert(phead); //先断言
ListNode* cur = phead->next; //然后将cur存储phead后面的节点的内容
while (cur != phead) //循环遍历去寻找
{
if (cur->data == x) //找到了就返回那个节点
{
return cur;
}
cur = cur->next;
}
return NULL; //没找到就返回空
}函数9:void ListInsert(ListNode* pos, LTDataTYpe x);//在pos节点的后面插入一个元素
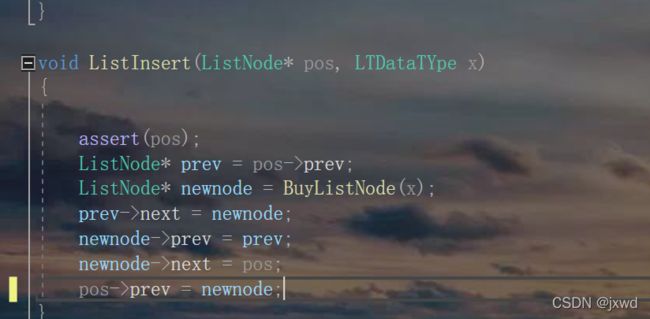
这个类比头插尾插就可以了
不做过多赘述
void ListInsert(ListNode* pos, LTDataTYpe x)
{
assert(pos);
ListNode* prev = pos->prev;
ListNode* newnode = BuyListNode(x);
prev->next = newnode;
newnode->prev = prev;
newnode->next = pos;
pos->prev = newnode;
}函数10:void ListErase(ListNode* pos);//删除pos节点
同样的道理,类比尾删、头删就可以了,没有必要赘述。
void ListErase(ListNode* pos)
{
assert(pos);
ListNode* prev = pos->prev;
ListNode* next = pos->next;
prev->next = next;
next->prev = prev;
free(pos);
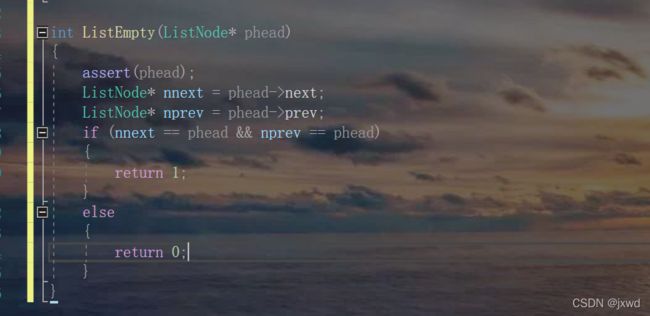
}函数11:int ListEmpty(ListNode* phead);//判断链表是否为空
就是直接判断一下phead的next和prev指针指向的是不是自己就可以了
是空就返回1;不是空就返回0
int ListEmpty(ListNode* phead)
{
assert(phead);
ListNode* nnext = phead->next;
ListNode* nprev = phead->prev;
if (nnext == phead && nprev == phead)
{
return 1;
}
else
{
return 0;
}
}函数12:int ListSize(ListNode* phead);//判断链表的大小(头节点是不算的)
函数13:void ListDestory(ListNode* phead);//销毁链表
void ListDestory(ListNode* phead)
{
assert(phead);
ListNode* cur = phead->next;
while (cur != phead) //循环遍历销毁
{
ListNode* pos = cur;
cur = cur->next;
free(pos);
}
free(phead); //再销毁头节点
}ok,截至此,我们将所有需要调用的函数逐个介绍完毕。
我们接下来就是用我们刚刚所写的函数来实现一下其功 能。看看我们所写的链表能不能用
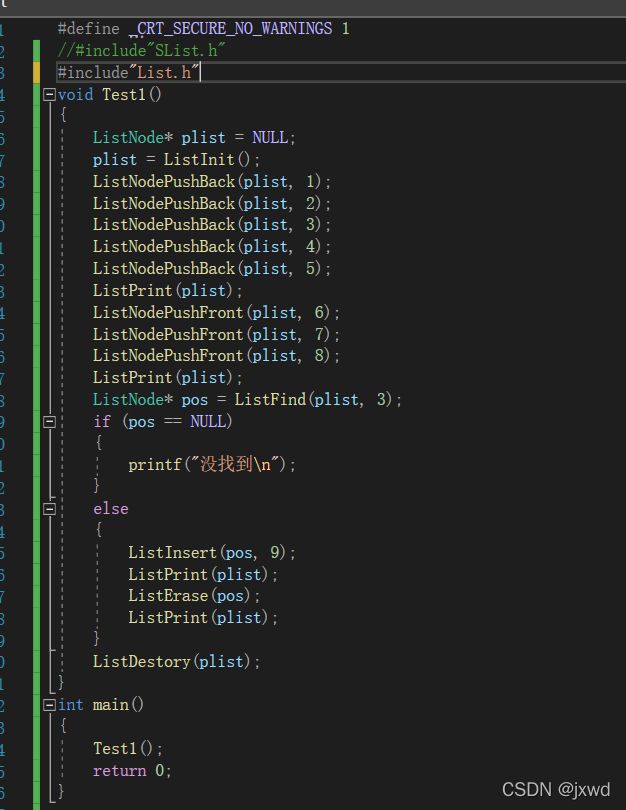
我们来写一个小程序:
#include"List.h"
void Test1()
{
ListNode* plist = NULL; //初始化一个结构体指针,并置空
plist = ListInit(); //赋成头指针
ListNodePushBack(plist, 1); //尾插
ListNodePushBack(plist, 2); //尾插
ListNodePushBack(plist, 3); //尾插
ListNodePushBack(plist, 4); //尾插
ListNodePushBack(plist, 5); //尾插
ListPrint(plist); 打印一下(第一次打印)
ListNodePushFront(plist, 6);//头插
ListNodePushFront(plist, 7);//头插
ListNodePushFront(plist, 8);//头插
ListPrint(plist); //打印一下(第二次打印)
ListNode* pos = ListFind(plist, 3); //寻找数据域为3的元素
if (pos == NULL)
{
printf("没找到\n");
}
else
{
ListInsert(pos, 9); //如果找到那就在后面插入9;
ListPrint(plist); //打印一下 (第三次打印)
ListErase(pos); //再删除该节点(数据域为3的)
ListPrint(plist); //再打印一下 (第四次打印)
}
ListDestory(plist); //销毁链表
}
int main()
{
Test1();
return 0;
}
我们的运行截图看一下:
完全如我们所愿。
那么,大功告成。
单链表的实现
有了上面的基础,我们再来看这个就很简单了,只是其没有头节点,用起来可能不是那么方便。
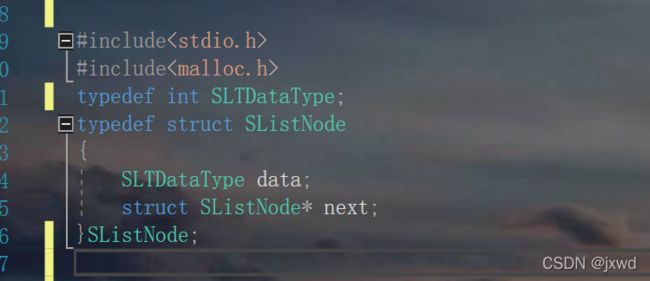
我们同样的道理,还是先创建一个节点:
#include
#include
typedef int SLTDataType;
typedef struct SListNode
{
SLTDataType data; //数据域
struct SListNode* next; //指针域
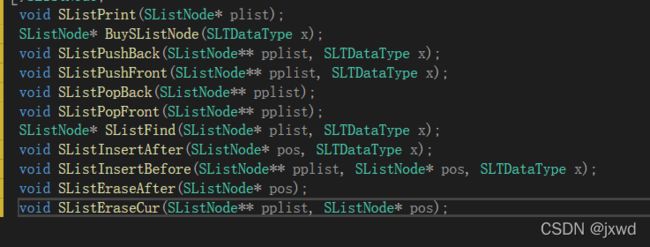
}SListNode; 这是我们接下来要实现的函数:
void SListPrint(SListNode* plist); //打印链表函数
SListNode* BuySListNode(SLTDataType x); //创建新节点
void SListPushBack(SListNode** pplist, SLTDataType x);//尾插
void SListPushFront(SListNode** pplist, SLTDataType x);//头插
void SListPopBack(SListNode** pplist); //尾删
void SListPopFront(SListNode** pplist); //头删
SListNode* SListFind(SListNode* plist, SLTDataType x); //寻找节点
void SListInsertAfter(SListNode* pos, SLTDataType x); //在目标节点的后面插入
void SListInsertBefore(SListNode** pplist, SListNode* pos, SLTDataType x);//在目标节点的前面插入
void SListEraseAfter(SListNode* pos); //删除pos节点的下一个节点
void SListEraseCur(SListNode** pplist, SListNode* pos); //删除pos节点
void SListDestory(SListNode* plist); //销毁链表(我们的思路是:给上一个创建节点函数,这样以后,在头增或者尾增等就可以直接调用该函数)
函数1:void SListPrint(SListNode* plist); //打印链表
void SListPrint(SListNode* plist);就一个参数:头节点的指针。
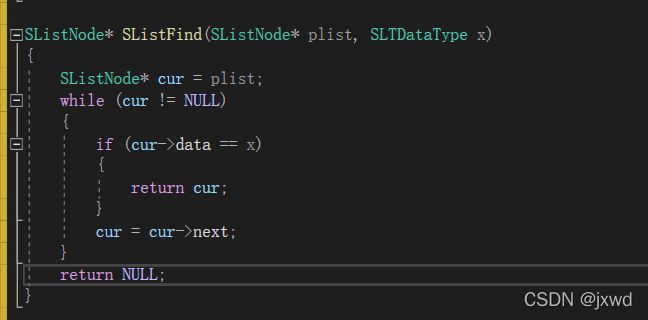
void SListPrint(SListNode* plist)
{
SListNode* cur = plist; //创建一个新的节点,然后将其存储起来
while (cur != NULL)
{
printf("%d ", cur->data); //依次打印
cur = cur->next;
}
printf("\n");
}函数2:SListNode* BuySListNode(SLTDataType x); //创建新节点
SListNode* BuySListNode(SLTDataType x);实现方法:
其实也是比较简单的,我们还是老样子,上代码,然后逐行解释:
SListNode* BuySListNode(SLTDataType x)
{
SListNode* node = (SListNode*)malloc(sizeof(SListNode));
//动态开辟一块空间(就是一个结构体)
node->data = x; //讲该节点的数据插入进其数据域中
//注意,在调用这个函数的时候是有一个参数x作为要增加的数据的
node->next = NULL;//先将其指针域置空
return node; //返回该动态开辟的空间
} 函数3:void SListPushBack(SListNode** pplist, SLTDataType x);//尾插
函数3:void SListPushBack(SListNode** pplist, SLTDataType x);//尾插
void SListPushBack(SListNode** pplist, SLTDataType x);注意一下这个函数的参数:第一个参数是第一个节点的二级指针(之所以传二级指针,是因为我们可能需要改变其指针域;而改变指针就需要传递二级指针)第二个参数就是需要传的数据域的值。
void SListPushBack(SListNode** pplist, SLTDataType x)
{
SListNode* newnode = BuySListNode(x);//创建新节点
if (*pplist == NULL) //如果pplist为空
{
*pplist = newnode; //那么newnode就是尾节点
}
else //如果不是空
{
SListNode* tail = *pplist; //先将pplist的内容先存储在tail里
while (tail->next != NULL)
{
tail = tail->next; //向后不断遍历,直到找到尾节点
}
tail->next = newnode; //在尾节点的后面插入新节点
}
}函数4:SListNode* SListPushFront(SListNode** pplist, SLTDataType x);//头插
SListNode* SListPushFront(SListNode** pplist, SLTDataType x);同样的道理,第一个参数是一个头节点的二级指针,第二个参数就是要传的数据域的值。
实现方法:
SListNode* SListPushFront(SListNode** pplist, SLTDataType x)
{
SListNode* newnode = BuySListNode(x);//创建新节点
if (*pplist == NULL) //如果其为空
{
*pplist = newnode; //那么其刚刚创建的节点就是头节点
}
else //如果不为空
{
SListNode* head = *pplist; //那么我们先创建一个head节点,让其存储pplist的内容
newnode->next = head; //让刚刚创建的节点的指针域指向head(即头节点)
}
return newnode; //返回头节点
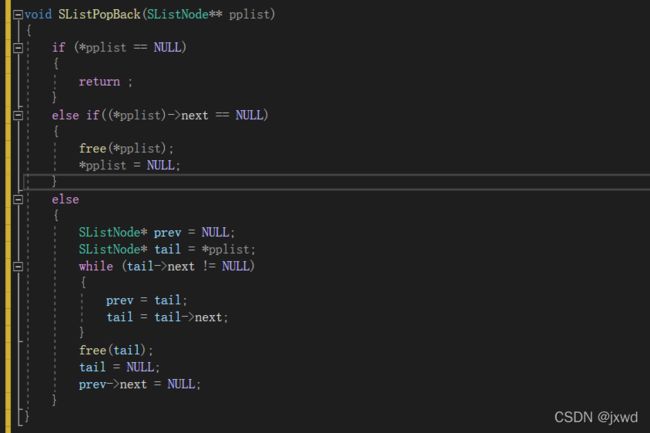
}函数5:void SListPopBack(SListNode** pplist); //尾删
这里的函数参数就是头指针(第一个节点的指针)
void SListPopBack(SListNode** pplist)
{
if (*pplist == NULL) //如果头节点其为空
{
return ; //直接返回
}
else if((*pplist)->next == NULL) //如果只有一个头节点
{
free(*pplist); //释放、置空、返回
*pplist = NULL;
}
else //否则
{
SListNode* prev = NULL;
SListNode* tail = *pplist; //设置 两个节点
while (tail->next != NULL) // 遍历,找尾
{
prev = tail;
tail = tail->next;
}
free(tail);
tail = NULL; //删除尾节点
prev->next = NULL;
}
}函数6:void SListPopFront(SListNode** pplist); //头删
void SListPopFront(SListNode** pplist)
{
if (*pplist == NULL)
{
return; //如果没有节点,直接返回
}
else
{
SListNode* next = (*pplist)->next; //把头节点的next节点存储起来
free(*pplist); //释放头节点
*pplist = next;
}
}函数7:SListNode* SListFind(SListNode* plist, SLTDataType x); //寻找节点
和双链表几乎一模一样,这里就不过多赘述
SListNode* SListFind(SListNode* plist, SLTDataType x)
{
SListNode* cur = plist;
while (cur != NULL)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
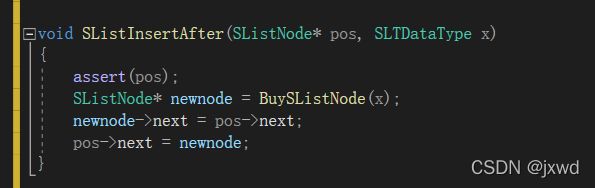
}函数8:void SListInsertAfter(SListNode* pos, SLTDataType x); //在目标节点的后面插入
这个比较简单,直接创建一个节点,然后就是三节点之间的关系(参照上面的动画)
void SListInsertAfter(SListNode* pos, SLTDataType x)
{
assert(pos);
SListNode* newnode = BuySListNode(x);
newnode->next = pos->next;
pos->next = newnode;
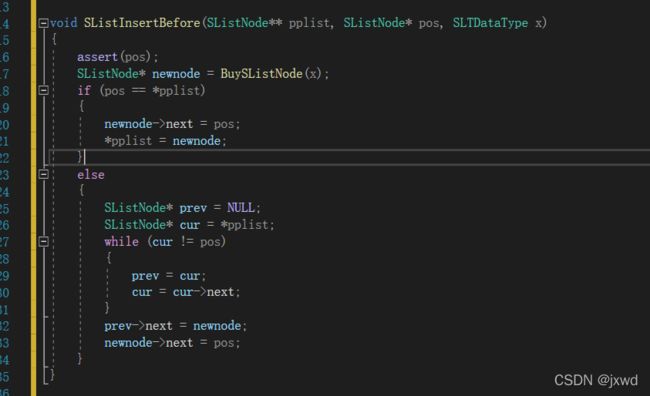
}函数9:void SListInsertBefore(SListNode** pplist, SListNode* pos, SLTDataType x);//在目标节点的前面插入
void SListInsertBefore(SListNode** pplist, SListNode* pos, SLTDataType x)
{
assert(pos);
SListNode* newnode = BuySListNode(x);
if (pos == *pplist) //判断pos节点是否是头节点
{
newnode->next = pos;
*pplist = newnode;
}
else //如果不是,那就找pos的前面的那个节点
{
SListNode* prev = NULL;
SListNode* cur = *pplist;
while (cur != pos)
{
prev = cur;
cur = cur->next;
}
prev->next = newnode;
newnode->next = pos; //然后老方法,三结点的关系交换
}
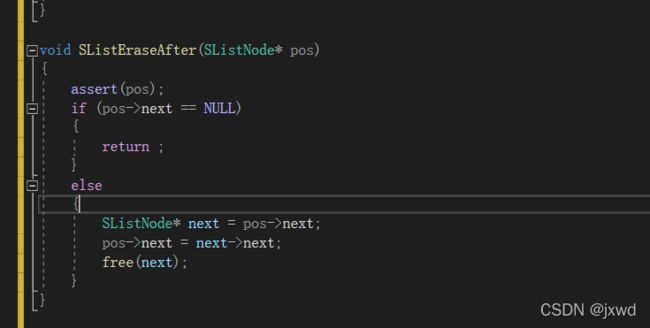
} 函数10:void SListEraseAfter(SListNode* pos); //删除pos节点的下一个节点
这个也是比较简单的,我们 就不再赘述。
void SListEraseAfter(SListNode* pos)
{
assert(pos);
if (pos->next == NULL)
{
return ;
}
else
{
SListNode* next = pos->next;
pos->next = next->next;
free(next);
}
}
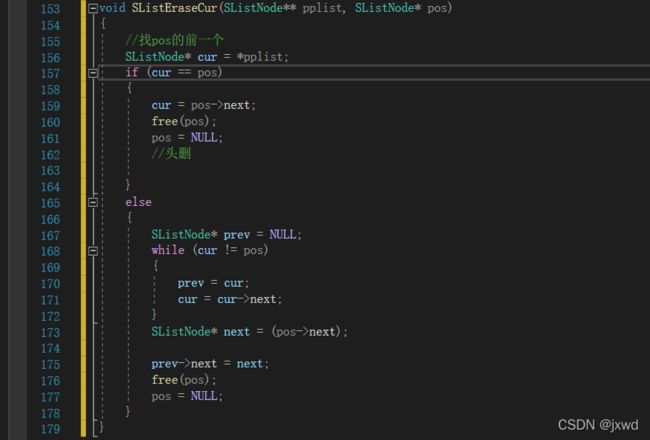
函数11:void SListEraseCur(SListNode** pplist, SListNode* pos); //删除pos节点
void SListEraseCur(SListNode** pplist, SListNode* pos)
{
//找pos的前一个
SListNode* cur = *pplist;
if (cur == pos)
{
cur = pos->next;
free(pos);
pos = NULL;
//头删
}
else //先要找到pos节点的前一个位置,然后将pos的信息(主要指指针域)
存储起来,让pos的前一个节点指向pos节点指向的节点
{ 然后再把pos节点删掉。
SListNode* prev = NULL;
while (cur != pos)
{
prev = cur;
cur = cur->next;
}
SListNode* next = (pos->next);
prev->next = next;
free(pos);
pos = NULL;
}
}
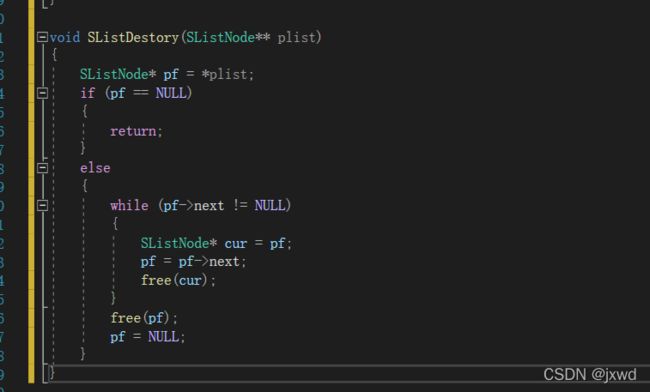
函数12:void SListDestory(SListNode** plist);//销毁链表
剧情和双链表一样的,就不再展示一遍了。
void SListDestory(SListNode** plist)
{
SListNode* pf = *plist;
if (pf == NULL)
{
return;
}
else
{
while (pf->next != NULL)
{
SListNode* cur = pf;
pf = pf->next;
free(cur);
}
free(pf);
pf = NULL;
}
}
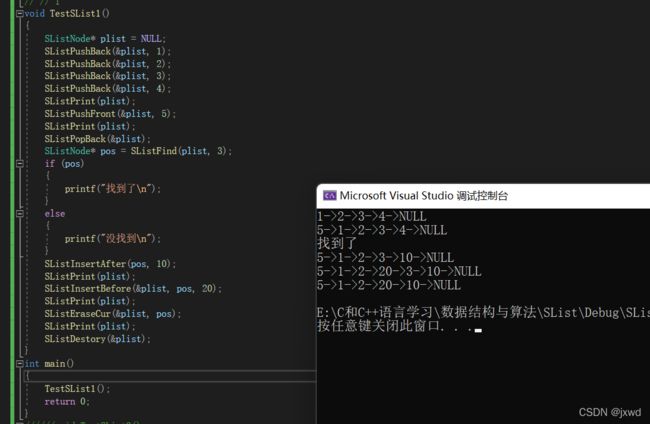
ok,我们现在来测试一下:
void TestSList1()
{
SListNode* plist = NULL;
SListPushBack(&plist, 1);
SListPushBack(&plist, 2);
SListPushBack(&plist, 3);
SListPushBack(&plist, 4); //尾插
SListPrint(plist); //打印
SListPushFront(&plist, 5); //头插
SListPrint(plist); //打印
SListPopBack(&plist); //头删
SListNode* pos = SListFind(plist, 3); //找节点
if (pos)
{
printf("找到了\n");
}
else
{
printf("没找到\n");
}
SListInsertAfter(pos, 10); //指定插入
SListPrint(plist);
SListInsertBefore(&plist, pos, 20); //指定插入
SListPrint(plist);
SListEraseCur(&plist, pos); //指定删除
SListPrint(plist);
SListDestory(&plist); //销毁链表
}
int main()
{
TestSList1();
return 0;
}到此为止,我们的所有函数全部完成,大功告成了。
如果你还想写更多的接口、实现更多的功能;或者是在现有的接口上玩出花样,那就留给读者自己了。
链表和顺序表的对比:
顺序表:
顺序表:一白遮百丑
白:空间连续、支持随机访问
丑:1.中间或前面部分的插入删除时间复杂度O(N)
2.增容的代价比较大。
链表:一(黑)毁所有
黑:以节点为单位存储,不支持随机访问
所有:
1.任意位置插入删除时间复杂度为O(1)
2.没有增容问题,插入一个开辟一个空间。
好啦,本期的内容就到这里啦,我们下期再见!!!
别忘了 关注 关注 + 关注呦