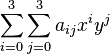双线性插值算法
图像的缩放很好理解,就是图像的放大和缩小。传统的绘画工具中,有一种叫做“放大尺”的绘画工具,画家常用它来放大图画。当然,在计算机上,我们不再需要用放大尺去放大或缩小图像了,把这个工作交给程序来完成就可以了。下面就来讲讲计算机怎么来放大缩小图象;在本文中,我们所说的图像都是指点阵图,也就是用一个像素矩阵来描述图像的方法,对于另一种图像:用函数来描述图像的矢量图,不在本文讨论之列。
越是简单的模型越适合用来举例子,我们就举个简单的图像:3X3的256级灰度图,也就是高为3个象素,宽也是3个象素的图像,每个象素的取值可以是0-255,代表该像素的亮度,255代表最亮,也就是白色,0代表最暗,即黑色。假如图像的象素矩阵如下图所示(这个原始图把它叫做源图,Source):
234 38 22
67 44 12
89 65 63
这个矩阵中,元素坐标(x,y)是这样确定的,x从左到右,从0开始,y从上到下,也是从零开始,这是图象处理中最常用的坐标系,就是这样一个坐标:
---------------------->X
|
|
|
|
|
∨Y
如果想把这副图放大为4X4大小的图像,那么该怎么做呢?那么第一步肯定想到的是先把4X4的矩阵先画出来再说,好了矩阵画出来了,如下所示,当然,矩阵的每个像素都是未知数,等待着我们去填充(这个将要被填充的图的叫做目标图,Destination):
? ? ? ?
? ? ? ?
? ? ? ?
? ? ? ?
现在从最简单的情况说起
1.最近邻插值
该算法是最简单的插值算法,就只是把放大后缺失的点的像素值用最靠近的原图的像素值直接填进去就可以了,比如坐标为(0,0),那么该坐标对应源图中的坐标可以由如下公式得出:
放大系数t=dstWidth/srcWidth=4/3
srcX=dstX/t, srcY = dstY/t
好了,套用公式,就可以找到对应的原图的坐标了(0/(4/3),0/(4/3))=>(0,0)
,找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。
接下来,如法炮制,寻找目标图中坐标为(1,0)的象素对应源图中的坐标,套用公式:
(1/0.75,0*0.75)=>(0.75,0)
结果发现,得到的坐标里面竟然有小数,这可怎么办?计算机里的图像可是数字图像,象素就是最小单位了,象素的坐标都是整数,从来没有小数坐标。这时候采用的一种策略就是采用四舍五入的方法(也可以采用直接舍掉小数位的方法),把非整数坐标转换成整数,好,那么按照四舍五入的方法就得到坐标(1,0),完整的运算过程就是这样的:
(1*0.75,0*0.75)=>(0.75,0)=>(1,0)
那么就可以再填一个象素到目标矩阵中了,同样是把源图中坐标为(1,0)处的像素值38填入目标图中的坐标。
依次填完每个象素,一幅放大后的图像就诞生了,像素矩阵如下所示:
234 38 22 22
67 44 12 12
89 65 63 63
89 65 63 63
这种放大图像的方法叫做最临近插值算法,这是一种最基本、最简单的图像缩放算法,效果也是最不好的,放大后的图像有很严重的马赛克,缩小后的图像有很严重的失真;效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真,比如,当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值,这种方法是很不科学的,当推得坐标值为0.75的时候,不应该就简单的取为1,既然是0.75,比1要小0.25 ,比0要大0.75,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的,这样才能达到更好的缩放效果。
2 双线性插值
双线型内插值算法就是一种比较好的图像缩放算法,它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,因此缩放效果比简单的最邻近插值要好很多。在双线性插值方法中源图片与目标图片的坐标转换关系和最近邻一样
双线性内插值算法描述如下:
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v)(其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数),则这个像素得值 f(i+u,j+v)可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) +uvf(i+1,j+1)
其中f(i,j)表示源图像(i,j)处的的像素值,以此类推。
比如,象刚才的例子,现在假如目标图的象素坐标为(1,1),那么反推得到的对应于源图的坐标是(0.75 , 0.75),这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素(1,1)的取值不能够由这个虚拟象素来决定,而只能由源图的这四个象素共同决定:(0,0)(0,1)(1,0)(1,1),而由于(0.75,0.75)离(1,1)要更近一些,那么(1,1)所起的决定作用更大一些,这从公式1中的系数uv=0.75×0.75就可以体现出来,而(0.75,0.75)离(0,0)最远,所以(0,0)所起的决定作用就要小一些,公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点。
双三次插值 用4*4个点赋予权重来构造 (未完待续。。。)
继续写
双三次插值(也称协调板元),二元双三次插值公式共有(3+1)2=16个系数,其一般形式可写成[9]:
a00 +a10x +a01y +a20x2 + a11xy + a02y2 +a21x2y + a12xy2 + a22x2y2 +a30x3 + a03y3 +a31x3y + a13xy3 + a32x3y2 +a23x2y3 +a33x3y3
双三次插值方法能够克服双线性插值和最邻近插值算法的缺点。计算精度比较高,插值效果较最近邻插值法和双线性插值法好,但是计算量大。在图像领域中,该方法考虑一个浮点坐标(i+u,j+v)周围的16个邻点,目标像素值f(i+u,j+v)可由如下插值公式得到:
f(i+u,j+v)=[A]×[B]×[C]
[A]=[S(u+1) S(u+0) S(u-1) S(u-2)]