深度学习——贝叶斯神经网络

前言

本文将总结贝叶斯神经网络，首先，我将简单介绍一下什么是贝叶斯神经网络（BNN）；接着我将介绍BNN是怎么训练的；然后我会介绍BNN背后的运作原理；最后，我将给出利用pytorch实现的BNN代码。

什么是贝叶斯神经网络

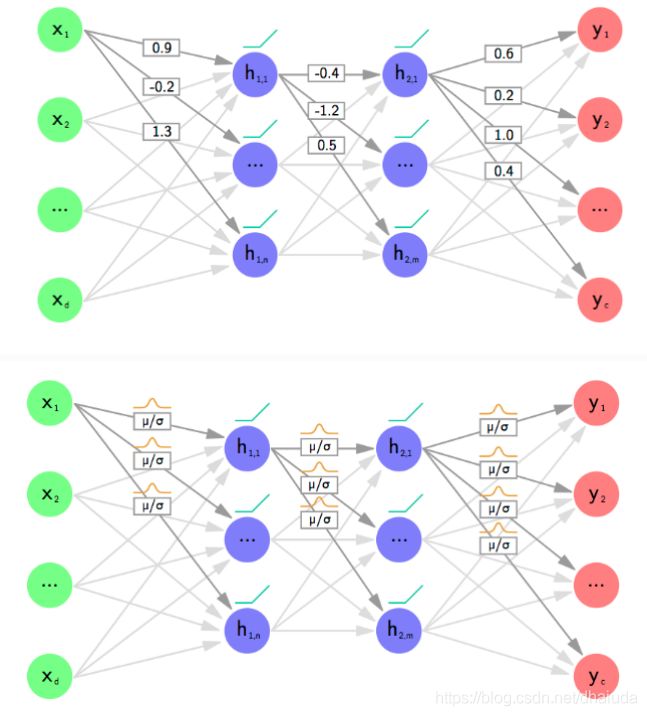
如上图，上半部分是反向传播网络，下半部分是贝叶斯神经网络。反向传播网络在优化完毕后，其权重是一个固定的值，而贝叶斯神经网络把权重看成是服从均值为$\mu$，方差为$\delta$的高斯分布，每个权重服从不同的高斯分布，反向传播网络优化的是权重，贝叶斯神经网络优化的是权重的均值和方差，所以贝叶斯神经网络需要优化的参数是反向传播网络的两倍。

在预测时，BNN会从每个高斯分布中进行采样，得到权重值，此时贝叶斯神经网络就相当于一个反向传播网络。也可以进行多次采样，从而得到多次预测结果，将多次预测结果进行平均，从而得到最终的预测结果（就像是ensemble模型）

How to train BNN

设训练集D为{$x_i,y_i$}，$0\le i\le N$，第$i$个权重$w_i$服从均值为${\mu }_i$，方差为${\delta }_i$的高斯分布，${\theta }_i$=$\{{\mu }_i,{\delta }_i\}$，BNN的输出为$y_{pred}$，BNN含有n个权重，则BNN的损失函数为

$$\begin{array}{rl}L(x_j)& =\sum _{i=1}^n[\log q(w_i|{\theta }_i)-\log p(w_i)]-\log p(y_j|W,x_j)\\ \log q(w_i|{\theta }_i)& =\log \frac{1}{\sqrt{2\pi }{\delta }_i}-\frac{(w_i-{\mu }_i{)}^2}{2{\delta }_i^2}\\ \log p(w_i)& =\pi (\log \frac{1}{\sqrt{2\pi }{\delta }_1}-\frac{(w_i{)}^2}{2{\delta }_1^2})\\ & +(1-\pi )(\log \frac{1}{\sqrt{2\pi }{\delta }_2}-\frac{(w_i{)}^2}{2{\delta }_2^2})\\ \log p(y_j|W,x_j)& =\log \frac{1}{\sqrt{2\pi }\delta }-(y_j-y_{pred}{)}^T{\delta }^{-1}(y_j-y_{pred})\\ & （回归任务中使用，分类任务个人认为用交叉熵）\end{array}\text{\hspace{1em}(1.0)}$$

BNN假设$q(w_i|{\theta }_i)$,$p(w_i)$,$\log p(y_j|w,x_j)$均服从高斯分布，由于中心极限定理的存在，这个假设是比较合理的。${\delta }_1、{\delta }_2、\delta 、\pi$均为超参数，需要自己指定。

我们通过采样得到$w_i$的具体值，从而计算1.0的各个式子。由于很难直接从$q(w_i|{\theta }_i)$采样，我们首先从标准正态分布中采样得到${ϵ}_i$，接着计算${\mu }_i+{ϵ}_i{\delta }_i$，从而得到服从$q(w_i|{\theta }_i)$分布的样本。

注意$L(x_j)$是针对一个训练样本$\{x_i,y_i\}$计算的，我们可以通过反向传播优化${\theta }_i$，但是反向传播有可能使得方差${\delta }_i$小于0，因此BNN对${\delta }_i$进行了特殊处理，如下所示
$${\delta }_i=\log (1+e^{{\rho }_i})$$
因此BNN的优化参数变为${\theta }_i=\{{\mu }_i,{\rho }_i\}$。

BNN背后的数学原理

神经网络用于建模分布$p(Y|X)$，即给定数据x，输出预测值y的分布，在分类任务中这个分布对应各个类别的概率；在回归任务中，一般认为是标准差固定的高斯分布，取均值作为预测结果。设训练集为$D$，我们对$p(Y|X)$进行如下变化

$$\begin{array}{rl}p(Y|X)& =\int p(Y|X,W)\frac{p(D)}{p(D)}dW\\ & =\int p(Y|X,W)\frac{p(WD)}{p(D)}dW\\ & =\int p(Y|X,W)p(W|D)dW\\ & =E_{p(W|D)}[p(Y|X,W)]\end{array}$$

$p(Y|X,W)$表示给定权重$w$和输入x，输出y的概率分布，其实就是神经网络。我们只需要依据训练集$D$建模出权重的分布$p(W|D)$，就可以依据蒙特卡罗方法，采样m个服从$p(W|D)$分布的样本，计算$\frac{1}{m}{\sum }_{i=1}^{m}p(Y|X,W_i)$,即可得到$p(Y|X)$。

可是$p(W|D)$往往难以计算，因此BNN使用变分估计，利用一个分布$q(W|\theta )$来逼近$p(W|D)$，利用KL散度度量$q(W|\theta )$、$p(W|D)$两个分布之间的相似性，则有

$$\begin{array}{rl}KL(q(W|\theta )||p(W|D))& =\int q(W|\theta )\log \frac{q(W|\theta )}{p(W|D)}dW\\ & =\int q(W|\theta )[\log q(W|\theta )-\log \frac{p(D|W)p(W)}{p(D)}]dW\\ & =\int q(W|\theta )[\log q(W|\theta )-\log p(D|W)-\\ & \log p(W)+\log p(D)]dW\\ & =E_{q(W|\theta )}[\log q(W|\theta )]-E_{q(w|\theta )}[\log q(D|W)]-\\ & E_{q(W|\theta )}[\log q(W)]+\log p(D)\end{array}$$

由于$\log p(D)$为已知分布，所以只需要最小化

$$E_{q(W|\theta )}[\log q(W|\theta )]-E_{q(W|\theta )}[\log q(D|W)]-E_{q(W|\theta )}[\log q(W)]\text{\hspace{1em}(2.0)}$$

一般训练集由标签Y和数据X两部分组成，故有
$$\begin{array}{rl}{E}_{q(W|\theta )}[\log q(D|W)]& =E_{q(W|\theta )}[\log q(X,Y|W)]\\ & =E_{q(W|\theta )}[\log \frac{q(WXY)}{q(W)}]\\ & =E_{q(W|\theta )}[\log \frac{q(Y|WX)p(WX)}{q(W)}]\\ & =E_{q(W|\theta )}[\log \frac{q(Y|WX)p(W)p(X)}{q(W)}](w与X相互独立)\\ & =E_{q(W|\theta )}\log q(Y|W,X)]+p(X)\end{array}\text{\hspace{1em}(3.0)}$$

由于$p(X)$为一个已知分布，将3.0代入2.0，优化目标变为

$$E_{q(W|\theta )}[\log q(W|\theta )]-E_{q(W|\theta )}[\log q(Y|W,X)]-E_{q(W|\theta )}[\log q(W)]\text{\hspace{1em}(4.0)}$$

给定一个训练数据$\{x_j,y_j\}$，对4.0使用蒙特卡罗法则可得

$$\sum _{i=1}^m\log q(W_i|\theta )-\sum _{i=1}^m\log q(y_j|W_i,x_j)-\sum _{i=1}^m\log q(W_i)\text{\hspace{1em}(5.0)}$$

假设5.0的m=1，BNN含有n个权重，第i个权重为$w_i$，第i个权重的高斯分布参数为${\theta }_i=\{{\mu }_i,{\delta }_i\}$，则有

$$\begin{array}{rl}\log q(W|\theta )=& \log q(w_1{w}_2...w_n|{\theta }_1{\theta }_2...{\theta }_n)\\ & =\log \frac{q(w_1{w}_2...w_n{\theta }_1{\theta }_2...{\theta }_n)}{q({\theta }_1{\theta }_2...{\theta }_n)}\\ & =\log \frac{q(w_1{\theta }_1)q(w_2{\theta }_2)....q(w_n{\theta }_n)}{q({\theta }_1{\theta }_2...{\theta }_n)}(w_i{\theta }_i之间相互独立)\\ & =\log \frac{q(w_1{\theta }_1)q(w_2{\theta }_2)....q(w_n{\theta }_n)}{q({\theta }_1)q({\theta }_2)...q({\theta }_n)}({\theta }_i之间相互独立)\\ & =\sum _{i=1}^n\log q(w_i|{\theta }_i)\end{array}\text{\hspace{1em}(6.0)}$$

由于$w_i$相互独立，则有
$$\log q(W)=\sum _{i=1}^n\log q(w_i)\text{\hspace{1em}(7.0)}$$

在m=1的情况下，将式6.0、7.0代入4.0可得
$$\sum _{i=1}^n[\log q(w_i|{\theta }_i)-\log p(w_i)]-\log p(y_j|W,x_j)\text{\hspace{1em}(8.0)}$$

8.0即1.0，至此，BNN的损失函数推导完毕，剩下一个采样问题，W服从$p(W|\theta )$分布，由于每个权重都服从一个高斯分布，且各个权重之间相互独立，所以$p(W|\theta )$是一个独立多元正态分布，独立多元正态分布由多个正态分布相乘得到，将各个正态分布中采样得到的样本点组合在一起得到的样本点将服从独立多元正态分布，所以采样时，权重$w_i$的样本点只需从$q(w_i|{\theta }_i)$采样即可（写程序时可以直接从独立多元正态分布中采样，这里如此表述只是为了方便理解）。

pytorch实现BNN

本节实现的BNN为一个单隐藏层神经网络，其输入大小为1，输出大小为1。用于拟合函数$-x^4+3x^2+1$进行回归预测

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Normal
import numpy as np

# BNN层，类似于BP网络的Linear层，与BP网络类似，一层BNN层由weight和bias组成，weight和bias都具有均值和方差
class Linear_BBB(nn.Module):
    """
        Layer of our BNN.
    """
    def __init__(self, input_features, output_features, prior_var=1.):
        """
            Initialization of our layer : our prior is a normal distribution
            centered in 0 and of variance 20.
        """
        # initialize layers
        super().__init__()
        # set input and output dimensions
        self.input_features = input_features
        self.output_features = output_features

        # initialize mu and rho parameters for the weights of the layer
        self.w_mu = nn.Parameter(torch.zeros(output_features, input_features))
        self.w_rho = nn.Parameter(torch.zeros(output_features, input_features))

        #initialize mu and rho parameters for the layer's bias
        self.b_mu =  nn.Parameter(torch.zeros(output_features))
        self.b_rho = nn.Parameter(torch.zeros(output_features))

        #initialize weight samples (these will be calculated whenever the layer makes a prediction)
        self.w = None
        self.b = None

        # initialize prior distribution for all of the weights and biases
        self.prior = torch.distributions.Normal(0,prior_var)

    def forward(self, input):
        """
          Optimization process
        """
        # sample weights
        # 从标准正态分布中采样权重
        w_epsilon = Normal(0,1).sample(self.w_mu.shape)
        # 获得服从均值为mu，方差为delta的正态分布的样本
        self.w = self.w_mu + torch.log(1+torch.exp(self.w_rho)) * w_epsilon

        # sample bias
        # 与sample weights同理
        b_epsilon = Normal(0,1).sample(self.b_mu.shape)
        self.b = self.b_mu + torch.log(1+torch.exp(self.b_rho)) * b_epsilon

        # record log prior by evaluating log pdf of prior at sampled weight and bias
        # 计算log p(w)，用于后续计算loss
        w_log_prior = self.prior.log_prob(self.w)
        b_log_prior = self.prior.log_prob(self.b)
        self.log_prior = torch.sum(w_log_prior) + torch.sum(b_log_prior)

        # record log variational posterior by evaluating log pdf of normal distribution defined by parameters with respect at the sampled values
        # 计算 log p(w|\theta)，用于后续计算loss
        self.w_post = Normal(self.w_mu.data, torch.log(1+torch.exp(self.w_rho)))
        self.b_post = Normal(self.b_mu.data, torch.log(1+torch.exp(self.b_rho)))
        self.log_post = self.w_post.log_prob(self.w).sum() + self.b_post.log_prob(self.b).sum()

        # 权重确定后，和BP网络层一样使用
        return F.linear(input, self.w, self.b)

class MLP_BBB(nn.Module):
    def __init__(self, hidden_units, noise_tol=.1,  prior_var=1.):

        # initialize the network like you would with a standard multilayer perceptron, but using the BBB layer
        super().__init__()
        # 输入为1，输出为1，只含有一层隐藏层的BNN
        self.hidden = Linear_BBB(1,hidden_units, prior_var=prior_var)
        self.out = Linear_BBB(hidden_units, 1, prior_var=prior_var)
        self.noise_tol = noise_tol # we will use the noise tolerance to calculate our likelihood

    def forward(self, x):
        # again, this is equivalent to a standard multilayer perceptron
        # 激活函数选用sigmoid
        x = torch.sigmoid(self.hidden(x))
        x = self.out(x)
        return x

    def log_prior(self):
        # calculate the log prior over all the layers
        return self.hidden.log_prior + self.out.log_prior

    def log_post(self):
        # calculate the log posterior over all the layers
        return self.hidden.log_post + self.out.log_post

    # 计算loss
    def sample_elbo(self, input, target, samples):
        # we calculate the negative elbo, which will be our loss function
        #initialize tensors
        outputs = torch.zeros(samples, target.shape[0])
        log_priors = torch.zeros(samples)
        log_posts = torch.zeros(samples)
        log_likes = torch.zeros(samples)
        # make predictions and calculate prior, posterior, and likelihood for a given number of samples

        # 蒙特卡罗近似
        for i in range(samples):
            outputs[i] = self(input).reshape(-1) # make predictions
            log_priors[i] = self.log_prior() # get log prior
            log_posts[i] = self.log_post() # get log variational posterior
            log_likes[i] = Normal(outputs[i], self.noise_tol).log_prob(target.reshape(-1)).sum() # calculate the log likelihood
        # calculate monte carlo estimate of prior posterior and likelihood
        log_prior = log_priors.mean()
        log_post = log_posts.mean()
        log_like = log_likes.mean()
        # calculate the negative elbo (which is our loss function)
        loss = log_post - log_prior - log_like
        return loss

def toy_function(x):
    return -x**4 + 3*x**2 + 1

# toy dataset we can start with
x = torch.tensor([-2, -1.8, -1, 1, 1.8, 2]).reshape(-1,1)
y = toy_function(x)

net = MLP_BBB(32, prior_var=10)
optimizer = optim.Adam(net.parameters(), lr=.1)
epochs = 2000
for epoch in range(epochs):  # loop over the dataset multiple times
    optimizer.zero_grad()
    # forward + backward + optimize
    loss = net.sample_elbo(x, y, 1)
    loss.backward()
    optimizer.step()
    if epoch % 10 == 0:
        print('epoch: {}/{}'.format(epoch+1,epochs))
        print('Loss:', loss.item())
print('Finished Training')

samples = 100
x_tmp = torch.linspace(-5,5,100).reshape(-1,1)
y_samp = np.zeros((samples,100))
for s in range(samples):
    y_tmp = net(x_tmp).detach().numpy()
    y_samp[s] = y_tmp.reshape(-1)

print("test result:",np.mean(y_samp, axis = 0))

参考文献

1、独立多元高斯分布
2、Variational inference in Bayesian neural networks
3、贝叶斯神经网络 BNN
4、浅析贝叶斯神经网络（Based on Variational Bayesian）
5、Bayesian Neural Networks：贝叶斯神经网络

如果您想了解更多有关深度学习、机器学习基础知识，或是java开发、大数据相关的知识，欢迎关注我们的公众号，我将在公众号上不定期更新深度学习、机器学习相关的基础知识，分享深度学习中有趣文章的阅读笔记。

如果您对增量学习感兴趣，欢迎关注我们的公众号，我将不定期在公众号上更新增量学习文章相关的阅读笔记