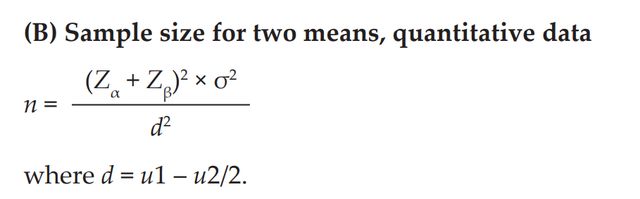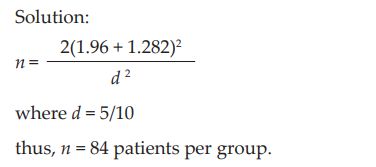样本量问题真的是好多人的老大难,是很多同学科研入门第一个拦路虎,今天给本科同学改大创标书又遇到这个问题,我想想不止是本科生对这个问题不会,很多同学从上研究生到最后脱离科研估计也没能把这个问题弄得很明白,那么希望大伙儿在看了这篇文章能够更加深入地理解样本量计算的逻辑,也能对大家的科研设计中的样本量设计部分有所启发。
样本量计算的逻辑
还记得我们最开始接触统计推断的时候,大家都知道一个词叫做原假设,原假设一般来讲都是“阴性的”,我们统计推断要做的事情便是推翻原假设从而得出有“统计学意义的结果”,怎么去推翻?就是在一次随机事件中小概率的我们认为不可能发生的符合备择假设的事件发生了,“不可能发生的事情竟然在现实中随便一次抽样研究中竟然就发生了”,就反证出原假设站不住脚,所以我们的结果就有“统计学意义”就得到了所谓的阳性结果了。
上面的这段话和样本量又如何扯上关系呢?继续往下看:
举个例子,比如现在两个研究团队都正在做一个性别比例的研究,两个团队都想通过自己的研究去证明世界上男性数量和女性数量不相等。(例子纯属虚构方便大家理解)
那么原假设就是世界上男性占比等于女性占比,现在两个研究团队都期望能用他们的抽样样本去推翻原假设,得到男性数量不等于女性数量的结论。
A团队为了省事将样本量定为了4个,那么A团队做一次研究最极端(可能性最小)的情况是4个全是同一个性别,那么此时这种最极端的情况发生的概率也为2*0.5^5=0.0625,其实也还不算我们通常认为的小概率(0.05),所以在4个样本量的情况下,A团队无论如何进行精妙的研究设计,并且A团队把这个设计精妙的研究无论重复多少次,都不可能得到阳性的研究结果,即使真实世界的男女比例真的不一样,A团队也100%发现不了阳性结果,就是因为样本量太小导致的。
大家好好体会下上面的例子,然后再看B团队的做法:
B团队就很鸡贼了,将样本量定为5个,此时最极端的情况是5个全是同一个性别,那么此时最极端的情况发生的概率为2*0.5^6=0.03125,哇,有点意思了,就是这个小概率事件理论上是可以发生的,而且,B团队只要有耐心,理论上重复100次该研究设计,大约会有3次都可以拒绝原假设,所以B团队如果在一次实验中刚好选的样本中5个都是同一性别,那么B团队就成功得到了阳性结果,但是仔细想想,如果真实世界中真的男女比例不一样,B团队因为样本量只有5个,所以仅仅只能寄希望5个样本全部是同性才能得到想要的结果,而且这种情况100次才大概能出现三次,是不是这个发现阳性结果的能力有点小呀?
就是即使真实世界中男女占比不一样,B团队也1-3%=97%的概率发现不了。
大家认真阅读上面我虚构的例子,你就能体会到,样本量估计的极端重要性以及几个可以影响样本量大小的指标:
分别是:
小概率事件的定义α,也就是显著性水平,我们的样本统计量达到了这个显著性水平就可以拒绝原假设(不管原假设是不是真)从而得到阳性结果,那么这就存在一种可能性就是原假设是真的话因为达到了显著性水平,你也把人家给拒绝了,这个就叫做一类错误;就是在前面的例子中,其实真实世界中男女比例是相等的,但是你就偏偏真的抽了5个全是同性的样本得到了男女比例不同的错误结论,如果这个时候你将α调低一点,这样的错误就会减少,比如调到0.3以下,那么在例子中B团队就不会拒绝原假设了,它需要更多的样本量才有可能拒绝原假设,同样的你也可以将α调高一点,这样A团队在理论上也可以得到男女数量不等的阳性结果。
我们知道了α是小概率事件的概率,相应地1-α为confidence level,就是就是假设做了无数次研究,每次研究都有相应的结局推断,那么1-α%的研究得到推断我们有信心认为一定是正确反应了真实情况的,或者说1-α%的研究样本估计值的某个区间一定是包含总体的真实值的。
统计效能1-β,也就前面例子中的能力,就是如果原假设真的为假,我可以正确拒绝原假设的能力,比如对于团队B来讲5个样本量的时候,理论上如果原假设为假,就是男女数量真的是不同的,5个样本量是可以得到拒绝原假设的结果的,但是只有在5人全为同性别的时候才能得到(只有2中情况,5个样本总的情况有2^5种,所以统计效能只有2/2^5,非常小),就是对于团队B来讲虽然理论上有能力得到阳性结果,但这个能力非常小,这个就叫做统计效能不足,我们一般期望统计效能能达到0.8,所以说团队B还是应该继续增加样本量。
统计效能1-β是如果原假设真的为假,我可以正确拒绝原假设的概率,那么自然你就理解了β就是原假设真的为假,却没能拒绝原假设的概率,叫做二类错误。
当然α和β不是本文的重点,但是希望看了上面的文字大家可以明白α和β为什么能影响样本量,我们继续思考,如果现在我们的研究变成了“是不是世界上的男(女)性比女(男)性多100%?”,此时是不是我的备择假设就成了“世界上性别构成比之差大于33.3%”,此时B团队5个样本理论上也不再能得到阳性的结果了。就是这个33.3%这个数也能影响样本量,这个叫做效应值d:
The size of the effect that is worthwhile to detect (d)
到这儿,推断统计的样本计算的逻辑基本上就给大家写完了(还有一个是总体的变异SD or σ,也会影响样本量,但在本例中不适用),本文的重点是教会大家如何计算统计推断的样本量和统计描述的样本量。
样本量计算的不同情形
我们先看统计推断的样本量估计,分两种情况,一种是以连续变量为结局,一种是以分类变量为结局,当结局是连续变量时,并且只有两组比较时(常见的RCT研究样本量计算都可以参照这个公式),有计算公式如下:
Gogtay N. J. (2010). Principles of sample size calculation. Indian journal of ophthalmology, 58(6), 517–518. https://doi.org/10.4103/0301-4738.71692
比如在下面的例子中应该是要85个样本(84.6)每组的:
上面的例子中给了标准差,但是这儿要特别注意d的计算,d的计算方法是均值差除以合并标准差:
This effect size is equal to the difference between the means at the endpoint, divided by the pooled standard deviation
但是合并标准差我们一般是不知道的,这个时候可以去找文献,去预试验,去大数据中挖掘或者直接极差/4估计一下,都是可以。
我们再看一个例子:
上面的例子是用PASS软件计算出来的样本量。依然是利用了了α,β,d和σ,得到的结果是85.
当结局是分类变量时,我们的计算公式如下:
参考文献如下:
Wang, H. and Chow, S.-C. 2007. Sample Size Calculation for Comparing Proportions. Wiley Encyclopedia of Clinical Trials.
依然是给大家一个例子:
一项研究欲探讨视频观察治疗(VOT)对结核病治疗是否优于直接监督治疗(DOT),随机化后2个月内是否完成80%或更多的预定治疗观察作为主要指标。预计VOT指标完成率为75%,DOT指标完成率为60%,检验效能为90%,检验水准为0.05,双侧检验,组间比例为1:1。试用PASS软件估算所需最小样本量。
上面的例子中,用PASS软件得到的样本量应该为200,如下图:
可以注意到,这个时候计算样本量用到了α,β,和d,就并没有σ,因为分类结局本身就不存在σ嘛。
样本量计算的R语言实操
刚刚给大家写了样本量的理论知识,以及在RCT中结局是连续变量和分类变量时样本量计算的实例。这部分教大家在R语言中进行相应的计算,R中有很多包可以帮助我们计算样本量,今天介绍pwr包。
比如我们的结局是连续变量时,连续变量部分给大家写的前面两个例子的样本量计算代码都如下:
pwr.t.test(n = NULL,
sig.level = 0.05, type = "two.sample", alternative = "greater", power = 0.90, d = 0.5)运行上面的代码即可得到样本量n为85和文献中和PASS软件的结果都是一样的:
当然啦,如果大家的实验是非劣效性试验或者优效性实验,只需要将alternaive参数改改就可以了。如果大家的实验两组不等,比如只定了对照组的人数,想要确定实验组多少人也是可以用pwr包的pwr.t2n.test计算的。
再看结局是分类变量时的样本量计算方法,这个时候要用到的函数是pwr.2p.test。比如上一部分例子中样本量PASS算出来是200,同样的我们用R语言写出如下代码:
pwr.2p.test(h = ES.h(p1 = 0.75, p2 = 0.60), n = NULL, sig.level = 0.05, power = 0.90, alternative = "two.sided")运行后我们可以看到,结果也是202(结果的些微不同是因为一个软件用的是normal approximation method,一个用的arcsine transformation,都不算错):
当然啦,如果大家的实验是非劣效性试验或者优效性实验,只需要将alternaive参数改改就可以了。如果大家的实验两组不等,比如只定了对照组的人数,想要确定实验组多少人也是可以用pwr包的pwr.2p2n.test计算的。
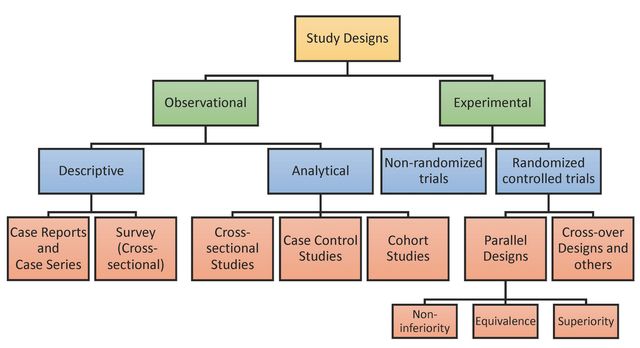
上面的整个逻辑是统计推断的样本量计算,但是整体看,我们样本量推断是有自己的流程的,如下:
第一步就是弄明白你的研究变量,比如你的研究就是一个现况调查,这个时候你关心的是样本量是不是能够正确地估计出总体参数,比如估计出总体均值,总体率的估计等等;比如你的研究是随机对照实验,你关心的是如果干预真的有效,你现有的样本量是不是有很大的把握识别出来有统计学意义的结果。
所以计算样本量之前你首先要弄明白你的研究要搞啥,不同的研究类型决定了样本量计算方法的不同:
其实做结果方程,做因子分析,做预测模型考虑的样本量东西又不一样了,反正大家要知道研究设计不同数据类型不同考虑的样本量又不一样了,但本文不展开。
本文只给大家写了RCT的样本量计算。
因为篇幅所限,描述统计的样本量,观察性研究的样本量计算就下回再写。
最后再给大家贴两篇文献,感兴趣的同学可以去瞅瞅:
Wang, X. and Ji, X., 2020. Sample size estimation in clinical research: from randomized controlled trials to observational studies. Chest, 158(1), pp.S12-S20.
Wang, X. and Ji, X., 2020. Sample size formulas for different study designs: supplement document for sample size estimation in clinical research.
小结
今天给大家写了统计推断样本量计算的原理和pwr包如何计算样本量,还有个叫Openepi的软件也可以计算样本量,PASS也可以计算样本量,而且这些都是免费的,大家可以择一使用。感谢大家耐心看完,自己的文章都写的很细,重要代码都在原文中,希望大家都可以自己做一做,请转发本文到朋友圈后私信回复“数据链接”获取所有数据和本人收集的学习资料。如果对您有用请先记得收藏,再点赞分享。
也欢迎大家的意见和建议,大家想了解什么统计方法都可以在文章下留言,说不定我看见了就会给你写教程哦,有疑问欢迎私信,有合作意向请莫要犹豫直接滴滴我。