计算机视觉与深度学习-线性分类器
以下内容是自己学习北京邮电大学鲁鹏副教授计算机视觉与深度学习课程(A02)的一些笔记,笔者能力有限,如有错误还望各位大佬在评论区批评指正 。
先贴一下课程的官网:CV-XUEBA
接上篇,简单的介绍了分类器的设计,接下来开启分类器的设计之旅。上篇地址:计算机视觉与深度学习-2
目录
1、线性分类器
1.1 数据集介绍
1.2 图像类型
1.3 图像输入
1.4 分类器的选择
1.5 什么是线性分类器?
1.6 线性分类器的决策
1.7 线性分类器的矩阵表示
1.8 线性分类器的权值向量
1.8 线性分类器的决策边界
2、损失函数
2.1 定义
2.2 多类支撑向量机损失
3、正则项与超参数
3.1 定义
3.2 L2正则项
4、优化算法
4.1 定义
4.2 梯度下降算法
4.3 梯度计算
5、数据集划分
6、K折交叉验证
7、数据预处理
1、线性分类器
1.1 数据集介绍
以CIFAR10为例子,这是一个公开的数据集。数据集包含50000张训练样本、10000张测试样本。有10个类别,飞机、鸟、猫、鹿、狗、蛙、马、船、卡车,均为彩色图像,大小是32*32。
1.2 图像类型
图像可分为二进制图像、灰度图像、彩色图像。二进制图像是由黑白两种颜色构成的图像,非黑即白;灰度图是每个像素都是1个byte,每个byte是0~255的值构成的图像,每个byte有256种可能性;彩色图像每个像素都是3个byte,代表R、G、B三个通道。
1.3 图像输入
大多数分类算法都要求输入向量。本课程是直接将每个像素点的rgb值依次写入向量中。对于CIFAR10而言,每一张图片的维度就是3072维(32*32*3)。
1.4 分类器的选择
我们选择从线性分类器开始,因为它形式简单、易于理解,同时通过层级结构(神经网络)或者高维映射(支撑向量机)可以形成功能强大的非线性模型。简单来说就是,线性分类器是神经网络和支撑向量机的基础。神经网络和支撑向量机是目前有效的两种分类方式,对于大样本而言,神经网络是绝对的王者之一,对于小样本来说,支撑向量机是绝对的王者之一。
1.5 什么是线性分类器?
线性分类器是一种线性映射,将输入的图像特征映射为类别分数。图中fi是线性分类器的分数,给系统一个样本,通过第i个类别的权值向量,第i个类别的偏置,就能得到这个样本在第i个类别的分数。需要注意的是![]() 的维度是和d的维度一致的。
的维度是和d的维度一致的。
1.6 线性分类器的决策
如果某一个样本在第i类的得分大于第j类那么就认为这个样本属于i类。
以下图为例,假设猫的这副图只有四个像素,分别为56,231,24,2。通过分类器后我们可以得到一组fi的得分,在猫类的得分最高,我们就认为这幅图里的是猫。
1.7 线性分类器的矩阵表示
写成矩阵后W有多少行是由类别个数决定的,有多少列是由x是多少维决定的。下图以CIFAR10为例介绍线性分类器的矩阵表示。 
1.8 线性分类器的权值向量
权值可以看成是一种模板,每个类别的模板都包含有这个类别的信息,W2的模板特别像车,而W8模板的马看起来有两个头,这是因为数据集中存在马头向左和向右两种朝向的马。当输入的图像与模板的相似程度越高时,得分就越高。
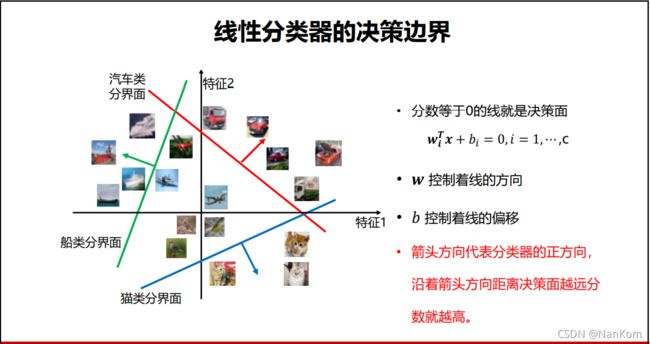
1.8 线性分类器的决策边界
分类任务在二维图像上表示就是分类器找到决策边界。样本掉在哪个决策边界的正向,就可以把它分为该类别。需要特别注意的是,沿着箭头方向越远离决策面,得分越高。
 2、损失函数
2、损失函数
2.1 定义
在度量W与b的好坏时,用到的是损失函数。损失函数搭建了模型性能与模型参数之间的桥梁,指导模型参数优化。它是一个函数,用来度量分类器的预测值与真实值的不一致程度,其输出值通常是一个非负实值。
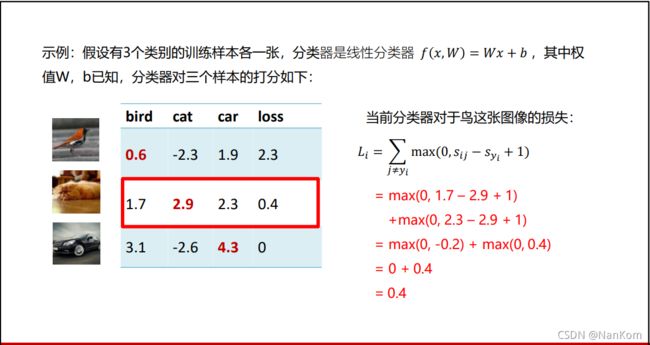
2.2 多类支撑向量机损失
Sij+1是为了防止噪声干扰等,加一以后Syi的得分还比它大,那么就可以认为第i个样本属于j类,增加了系统的稳定性。需要注意的是,正确类别的得分比不正确类别的得分高出一分,就认为没有损失,否则就会产生损失。
来看一个例子:这个分类器在对第二幅图是猫的打分最高,但是还是存在损失,因为对猫的打分并没有比车的打分高出一分,所以还是存在损失。(勘误:把鸟改成猫)
3、正则项与超参数
3.1 定义
由于使损失函数L=0的W并不一定,所以在选择W时引入了正则项。正则损失是为了防止模型在训练集上学习得太好,即过拟合。R(W)是一个与权值有关,跟图像数据无关的函数,![]() 是一个超参数,控制着正则损失在总损失中所占的比重。
是一个超参数,控制着正则损失在总损失中所占的比重。
不是通过学习得到的参数,而是开始学习前设置的参数,就是超参数。超参数一般对模型有着重要的影响。
3.2 L2正则项
L2正则项即R(W)是W的每一项元素平方再求和。对于示例,我们可以看到,这个样本分类器输出是一样的,而正则损失不同,R(W2)的值更小。因此我们会倾向于选择分类器2,原因在于W2的权值让x的每一个维度都参与运算,在真实提取中,即使在提取数据时某一维出错,但是考虑了所有的特征每一维都参与了运算,这样系统的容错性就提升了。对于分类器1而言由于并不是每一维都参与运算,所以分类器1很容易出错。这都是因为平方引起的,如果权值越集中则平方项越大,损失就越大。
4、优化算法
4.1 定义
参数优化是机器学习的核心步骤之一,它利用损失函数的输出值作为反馈信号来调整分类器参数,以提升分类器对训练样本的预测性能。优化的目标就是找到使损失函数L达到最优的那组参数W。
4.2 梯度下降算法
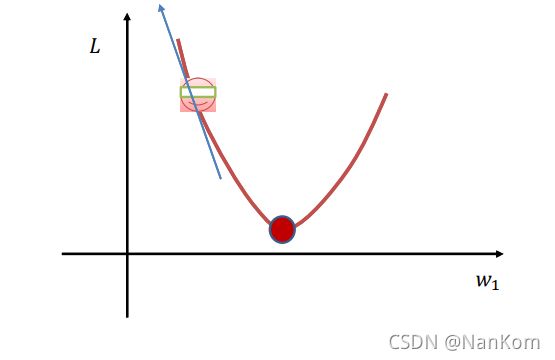
我们可以借助这幅图来理解,优化算法就是为了找到最优的参数,也就是当L 最小的时候。小人只需要往上或者往下走,然后摸摸上面和下面来判断自己是往下走了还是往上走了。但是这里有一个问题,就是走的步长该多大,如果步子迈大了,就过了最低点,太小了速度太慢,而这个步长就是我们说的学习率。学习率对学习起着举足轻重的作用。这是梯度算法的核心,也是神经网络最难调的参数。
优化的思路就是,通过计算梯度得到当前的权值梯度(梯度方向),然后再用当前的权值(当前位置)减去学习率乘权值梯度的积,最后输出新的权值(位置),循环计算,直到新的权值与之前的权值相差很小时结束,就完成了分类器的学习。
4.3 梯度计算
梯度计算有两种方法,数值法和解析法。数值法得到的是近似值,通常不使用数值法,因为其对于复杂的算法计算量太大且不准确。
因此一般使用解析法,而数值梯度可以用来校验解析梯度的正确性。
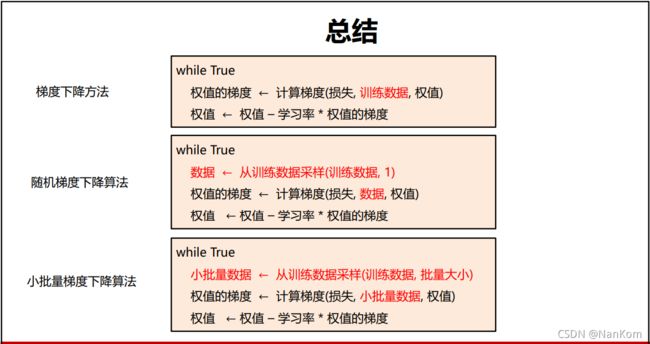
但是对于N很大时,更新一次权值耗费时间很长,计算速度很慢。而随机梯度下降算法可以很快的完成迭代,即每次随机选择一个样本,计算损失并更新梯度。但是也有可能会出现负优化的情况,因为样本可能存在噪声等,不过在实际操作中可以很快的降到“谷底”。
还有小批量梯度下降算法,每次随机选择m个样本。需要注意的是,m是一个超参数,一般是2的幂数。有几个名词 iteration:表示1次迭代,每次迭代更新1次网络结构的参数。batch-size:1次迭代所使用的样本量,即m。epoch:1个epoch表示过了一遍训练集中的所有样本。
5、数据集划分
一般来说,数据集会被分为训练集和测试集,训练集用来训练模型,测试集用来检验模型,评估泛化能力。但是对于很多任务中,由于有超参数,并不能简单的划分数据集。因此在实际操作中,应该把数据集分为三份,训练集、验证集、测试集。验证集用于确定超参数。
6、K折交叉验证
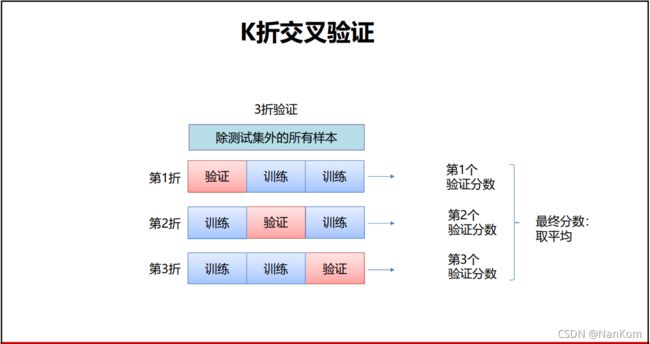
如果数据太小,那么很可能验证集包含的样本就太少,从而无法在统计上代表数据。可能导致验证集两次给出的精度相差很大,这个时候就可以用K折的交叉验证。K折代表划分的个数。如果是三折验证,在某个超参数下,第一次用第一个样本验证,第二次用第二个样本验证,第三次用第三个样本验证,最后得到的分数求平均。还可以在每次验证之前将数据打乱,就是带有打乱的K折交叉验证。
7、数据预处理
通常我们不会用原始数据去训练,而是对数据取平均(数值范围操作)和归一化(去量纲)处理,去相关(降维)和白化(去相关后归一化)。