R语言-岭回归的代码与案例解读

应用岭回归的场景有很多。
本文介绍的是 在应用多元线性回归时 遇到多重共线性问题，且无法删除变量或者增加样本量的情况下，应用岭回归的情况。

• 案例：互联网经济对中国经济增长影响
• 基础模型：C-D生产函数：Y=A*L^α *K^β
• 应用模型：岭回归
• 使用工具：r语言
• 使用程序包：‘MASS’、‘xlsx’、‘car’
• 准备数据：Y：国民生产总值、K：固定资产投资；L:年期末就业人数；A：互联网综合发展水平
• 数据处理：为了模型的稳定性与计算的简易性，分别对两端取对数，变成线性关系，得到最终模型：lnY=γlnA+αlnL+βlnk
• 变量解释与结果推测：综合考虑互联网经济的指标体系和数据的可得性，采用因子分析的方法估计综合技术水平A（详情可点击）。γ、α、β表示互联网经济产出弹性系数、劳动力弹性和资本弹性系数，本文推测，生产弹性系数会符合以下估计：
  （1）α+β+γ>1，表示最终经济规模呈递增趋势；
  （2）α<1、β<1，表示边际收益递减的规律性，γ>1，表示互联网经济的边际收益递增性，符合互联网经济的特征。

对数线性化与多重共线性判别

#加载程序包与数据
library(MASS)
library(xlsx)
library(car)
y <- read.xlsx("D:/RData/sets/Y.xlsx",1,encoding = "UTF-8")
l <- read.xlsx("D:/RData/sets/L.xlsx",1,encoding = "UTF-8")
a <- read.xlsx("D:/RData/sets/A.xlsx",1,encoding = "UTF-8")
k <- read.xlsx("D:/RData/sets/K.xlsx",1,encoding = "UTF-8")
dataY <-(y,a,l,k)
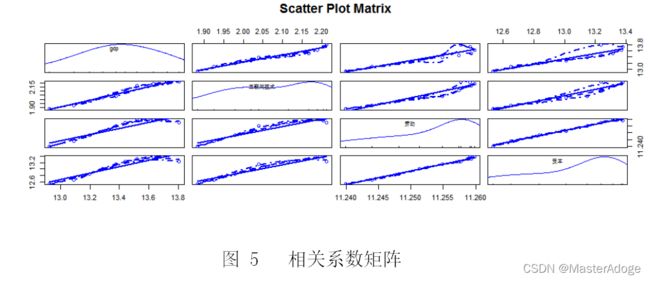
#得到相关系数矩阵：变量之间呈同向变动的关系，符合经济发展的规律
scatterplotMatrix(dataY,spread=FALSE,smoother.args=list(lty=2),main="Scatter Plot Matrix")

#数据对数化
ly <- log(y)
la <- log(a)
ll <- log(l)
lk <- log(k)
dY <-data.frame(ly,la,ll,lk)
#做最小二乘回归
fit <- lm(gdp~a+l+k,data=dataY)
fit
summary(fit)

用最小二乘法建立计量模型，由（表6）看到，虽然模型的拟合优度足够高，F值也很大，整体拟合效果好，但是模型系数检验不显著。显而易见考虑模型的多重共线性问题

• 多重共线性是指在除了因变量与自变量的关系外，在解释变量之间也存在线性相关关系的一种形式。多重共线性导致gdp与互联网综合发展水平、劳动和资本之间的关系不显著。

#应用vif值的开方来判断是否存在多重共线性
library(car)
vif(fit)
sqrt(vif(fit))>2
#vif值开方远大于2，存在多重共线性。

• 岭回归是一种有偏估计，虽然对数据的无偏估计不准确，但是可以更准确的得到α，β，γ之间的系数关系。

#首先用岭迹图判断k值区间并使用GCV值来进行岭回归估计
plot(lm.ridge(dY[,1]~dY[,2]+dY[,3]+dY[,4],data = dY,lambda = seq(0,0.5,0.001)))
#确定k至的估计区间在0-0.5间

#确定k值并选择GCV值=0.127.做岭回归。
select(lm.ridge(dY[,1]~dY[,2]+dY[,3]+dY[,4],data = dY,lambda = seq(0,0.5,0.001)))
ridge1 <- lm.ridge(dY[,1]~dY[,2]+dY[,3]+dY[,4],data = dY,lambda =0.127)
ridge1 <- lm.ridge(gdp~a+l+k,data = dY,lambda =0.127)
ridge1

结果分析

从系数符号看，符合我们前面对本模型的系数估计。即弹性系数之和大于1，互联网技术弹性系数大于1，劳动力弹性系数和资本弹性系数小于1。从整体来看，α+β+γ大于1，表明了边际产量递增的趋势，符合当前经济发展的现状，当国家投入劳动力和资本和技术时，经济发展水平总量增加。
（分别具体的每个系数分析在这里不做过多讲述）
本文结论为：我国正处于技术推动经济发展的新时代，应以互联网技术为核心，结合信息与知识，对我国经济发展做出贡献。

总结

本文以具体案例为例子，讲解了岭回归模型的r语言实现过程，并对案例进行一定程度的分析。希望可以对大家有帮助。

在本文中对互联网综合发展指数的因子分析求解可以看该连接：
http://t.csdn.cn/q3q9O