一篇线段树 从入门到进阶 实现原理与代码模板

一、线段树入门

线段树是什么呢？简单来说就是既方便我们求一个数组某区间的和，又方便我们修改数组的某个元素的一种数据结构。属于二叉搜索树。

对于一个普通数组来说，我们修改某一元素的时间复杂度是O(1)，但求某区间和的时间复杂度是O(n)。
若使用前缀和数组，我们求某区间和的复杂度是O(1)，但我们修改某一元素的复杂度是O(n)。
为了方便我们又修改又求和，我们就使用线段树来均衡这两个操作的复杂度，把他们都平均到O(logn)。

线段树他是一个树形结构的数组，看一下下面这个结构图你就会很清楚的理解什么是线段树了。

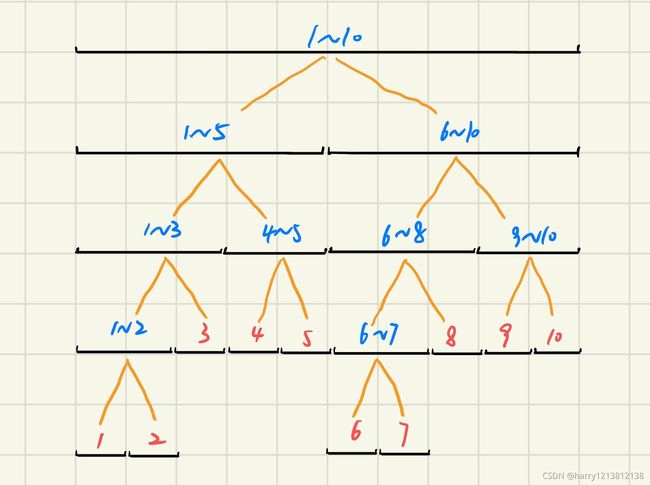
红色是叶子结点，他的每一个结点存的是该区间的和。而每一个结点是一个线段（区间），因此这种树形结构我们把他叫做线段树。每一个结点都有左右两个儿子（分别存该结点的左一半区间和右一半区间）。而除了最下面的一层，这个树就是一个满二叉树。

了解完线段树的结构之后，我们来考虑一下用什么来存储这个树呢。我们一般是用一个数组来模拟这棵树，因为他除了最后一层外是一个满二叉树，有很多性质非常好使用，并且用数组存会比用指针的树形结构更方便。我们一般设根节点为数组下标为1，即根为tr[1]。
而对于任意一个节点来说，假设他的下标为x，则他左儿子的下标就是2x，他右儿子的下标就是2x+1，他父结点的下标就是$\lfloor \frac{x}{2}\rfloor$。假设该结点存的是[l,r]的区间和，那么他的左儿子存的是[l,mid]的区间和、右儿子存的是[mid+1,r]的区间和（mid=(l+r)/2）。
若要存区间长度为$n$的线段树，我们需要的结点数最多是$4n-1$个，因此我们一般给数组开$4n$大小的空间。

---

适用范围

通过了解线段树的结构，我们可以发现线段树其实就是分块的思想，只不过他最多分log层，而且每次查询最多会访问两条链，因此他的时间复杂度很低，比分块小得多。但同样因为这个结构他也有了一些限制，他只能用于具有结合律的性质的求解，比如我要求某个区间的某个属性，它可以由其两个子区间的属性相结合方可。例如sum求和操作（sum(x) = sum(son1) + sum(son2)），max/min区间最值操作、xor异或操作、乘积操作、求区间内素数个数等等。

---

实现原理

线段树的主要操作有修改元素（modify），求区间和（query）。主要的函数还有一个建树函数（build），向上更新（pushup）。基础线段树主要实现了单点修改与区间求和。

对于修改操作（modify） 来说，我们先从根节点向下不断递归找到我要修改的那个点（叶子结点），然后再一层一层向上返回，修改路径上的每一个结点。假设我给该数+k，那么我在路径上的每一个结点都+k，就完成了修改操作。
对于询问操作（query） 来说，我们根据目标区间和当前结点区间的关系，逐步找到需要的目标区间，然后返回答案。
对于pushup操作来说，他是线段树的关键，因为不管用线段树求什么，都是一样的访问方式，但是在修改完某个点之后或是build后，我们要向上修改它的每个父结点，因此就会执行不同的pushup操作。
对于build操作来说，就是最开始的建树，将原数组建成线段树。访问到叶子结点后向上pushup。

我们一般用x << 1来求左儿子（相当于2x），x << 1 | 1来求右儿子（相当于2x+1），x >> 1来求父结点（看着高级 ）。

基本函数都用递归的思想，具体解释见代码。

---

代码模板及详解

模板题：AcWing 245. 你能回答这些问题吗

模板题：AcWing 1275. 最大数

#include
#include
#include
#include
#define x first
#define y second
using namespace std;
const int N = 1000000;
typedef long long LL;

int n,m,p,last,op,tree[N];		//tree数组来存线段树
char ch;

void build(int x,int tl,int tr)	//建树操作，由于该题是一个一个加入的，不需要建树操作
{
	if(tl == tr)
		return;//tree[x] = arr[tl];
	int mid = tl+tr >> 1;
	build(x << 1,tl,mid);		//递归走左儿子
	build(x << 1 | 1,mid+1,tr);	//递归走右儿子
}

void pushup(int u)		//pushup操作，该题是求区间最大值，因此父亲的值等于左右儿子中最大的一个
{
	tree[u] = max(tree[u<<1],tree[u<<1|1]);		//父亲的值等于左右儿子中最大的一个
}

void modify(int u,int tl,int tr,int x,int k)	//修改操作，u是树上的当前结点，[tl,tr]是树上该结点所代表的区间，给x位置的数修改为k
{
	if(tl == tr)	//如果tl和tr相等说明到了叶子结点了，即要找的点
	{
		tree[u] = k;	//修改当前结点为k
		return;
	}
	int mid = tl+tr >> 1;	//求出mid
	if(x > mid)		//如果要改的点在右半边
		modify(u << 1 | 1,mid+1,tr,x,k);	//往右递归，注意右儿子代表的区间是[mid+1,tr]
	else			//否则就在左边
		modify(u << 1,tl,mid,x,k);	//往左递归，左儿子代表的区间是[tl,mid]
	pushup(u);		//pushup往上修改父结点
}

int query(int u,int tl,int tr,int l,int r)	//查询操作，u是当前结点，[tl,tr]是该结点所代表的区间，[l,r]是我的目标查询区间
{
	if(tl >= l && tr <= r)	//如果查询的区间将该结点的区间完全包含，直接返回该结点的值
		return tree[u];
	int mid = tl+tr >> 1,v = 0;
	if(l <= mid)		//如果查询的区间和该结点的左儿子有重合
		v = query(u << 1,tl,mid,l,r);	//接着查询左儿子
	if(r > mid)			//和右儿子有重合
		v = max(v,query(u << 1 | 1,mid+1,tr,l,r));	//接着查询右儿子，并取左右儿子中的最大值
	return v;	//返回
}

int main()
{
	cin >> m >> p;
	//build(1,1,m);		//该题不需要建树操作
	for(int i = 0;i < m;i++)
	{
		cin >> ch;
		if(ch == 'Q')	//如果是查询
		{
			cin >> op;
			last = query(1,1,m,n-op+1,n);	//查询从1号根结点开始，根结点的区间是[1,m]
			cout << last << endl;
		}
		else
		{
			cin >> op;
			modify(1,1,m,n+1,((LL)last+op)%p);	//修改也从根结点开始
			n++;
		}
	}
	
	return 0;
}

---

二、线段树的进阶

这里主要实现了区间修改及单点查询

这里主要用pushdown函数实现懒标记，若要对某一区间进行修改（都+k），我们一个一个循环单点修改复杂度太高，太麻烦，这里我们用一个懒标记（lazytarget）记作lz标记。当我们搜索到当前区间在目标区间内部时，我们给该区间加上（end-start+1）* k，并标记该区间（lz= k），下次若查询该区间内的某值时，只需加上长度*k即可。

pushdown和pushup是相对应的，pushup是由子结点修改父结点的操作；而pushdown是由父结点来修改子结点的操作。

我这里规定lz标记记得是当前结点的所有子结点都加lz，当前结点不加（这个只需统一即可）。

具体见代码：

代码解析

模板题：AcWing 243. 一个简单的整数问题2

#include 
#include 
#include 
using namespace std;
const int N = 100010;
typedef long long LL;

int n,m,w[N];
LL d;
struct Node{
	int l,r;
	LL sum,lz;
}tree[N*4];

void pushup(int u)
{
	tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum;
}

void pushdown(int u) //我们规定懒标记记的都是子结点要加的值，当前结点已经加过了
{
	if(tree[u].lz)		//如果当前结点有懒标记的话
	{
		Node &root = tree[u],&left = tree[u << 1],&right = tree[u << 1 | 1];		//将当前结点记作root，左儿子记作left，右儿子记作right
		left.sum += (LL)(left.r-left.l+1) * root.lz;	//左儿子加上懒标记的和（区间长度*lz）
		left.lz += root.lz;		//左儿子加上懒标记
		right.sum += (LL)(right.r-right.l+1) * root.lz;	//右儿子加上懒标记的和
		right.lz += root.lz;	//右儿子加上懒标记
		root.lz = 0;	//当前结点的标记一定要清零
	}
}

void build(int u,int l,int r)
{
	if(l == r)
		tree[u] = {l,r,w[l],0};
	else
	{
		tree[u] = {l,r};
		int mid = l + r >> 1;
		build(u << 1,l,mid);
		build(u << 1 | 1,mid+1,r);
		pushup(u);		//建树后pushup
	}
}

void modify(int u,int l,int r,int k)
{
	int tl = tree[u].l,tr = tree[u].r;
	if(tl >= l && tr <= r)
	{
		tree[u].sum += (tree[u].r-tree[u].l+1) * k;
		tree[u].lz += k;
	}
	else
	{
		pushdown(u);		//修改操作执行前一定要先向下分裂
		int mid = tl+tr >> 1;
		if(l <= mid)
			modify(u << 1,l,r,k);
		if(r > mid)
			modify(u << 1 | 1,l,r,k);
		pushup(u);			//修改完再向上修改
	}
}

LL query(int u,int l,int r)
{
	int tl = tree[u].l,tr = tree[u].r;
	if(tl >= l && tr <= r)
		return tree[u].sum;
	pushdown(u);		//询问前一定要向下传
	int mid = tl+tr >> 1;
	LL res = 0;
	if(l <= mid)
		res += query(u << 1,l,r);
	if(r > mid)
		res += query(u << 1 | 1,l,r);
	return res;
}

int main()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i++)
		cin >> w[i];
	build(1,1,n);
	char c;
	int l,r;
	while(m--)
	{
		cin >> c >> l >> r;
		if(c == 'Q')
			cout << query(1,l,r) << endl;
		else
		{
			cin >> d;
			modify(1,l,r,d);
		}
	}
	
	return 0;
}

总结： 建树后一定要pushup，修改完一定要pushup；修改前一定要pushdown，查询前一定要pushdown，各做两遍。

---

三、线段树经典习题

传送门： 区间最大公约数