leetcode-二叉树的遍历-前序遍历/中序遍历/后序遍历/层序遍历 (C++代码)
二叉树的遍历-前序遍历/中序遍历/后序遍历/层序遍历 (C++代码)
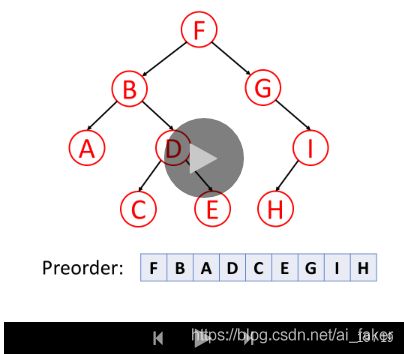
1.前序遍历
前序遍历首先访问根节点,然后遍历左子树,最后遍历右子树。
请看下面的例子:
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,2,3]
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector res;
preorder(root, res);
return res;
}
void preorder(TreeNode *root, vector &res) {
if (!root)
return;
res.push_back(root->val);
if (root->left)
preorder(root->left, res);
if (root->right)
preorder(root->right, res);
}
};
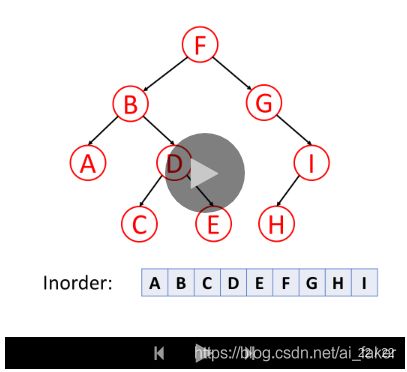
2.中序遍历
中序遍历是先遍历左子树,然后访问根节点,然后遍历右子树。
让我们一起来看树的中序遍历:
通常来说,对于二叉搜索树,我们可以通过中序遍历得到一个递增的有序序列。
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
vector res;
midorder(root, res);
return res;
}
void midorder(TreeNode* root, vector &res){
if(!root)
return;
if(root->left)
midorder(root->left, res);
res.push_back(root->val);
if(root->right)
midorder(root->right, res);
}
};
3.后序遍历
后序遍历是先遍历左子树,然后遍历右子树,最后访问树的根节点。
我们一起来看后序遍历的动画演示:
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
vector res;
afterorder(root, res);
return res;
}
void afterorder(TreeNode *root, vector &res){
if(!root)
return;
if(root->left)
afterorder(root->left, res);
if(root->right)
afterorder(root->right, res);
res.push_back(root->val);
}
};
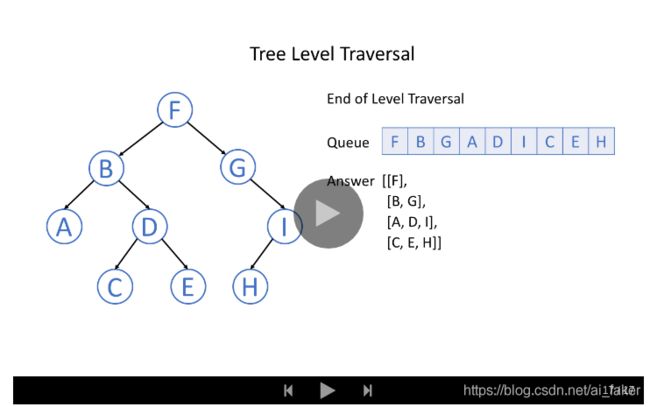
4.层序遍历
4.1预备知识
C++之queue容器使用
queue 模板类的定义在头文件中。
与stack 模板类很相似,queue 模板类也需要两个模板参数,一个是元素类型,一个容器类
型,元素类型是必要的,容器类型是可选的,默认为deque 类型。
定义queue 对象的示例代码如下:
queue<int> q1;
queue<double> q2;
queue 的基本操作有:
入队,如例:q.push(x); 将x 接到队列的末端。
出队,如例:q.pop(); 弹出队列的第一个元素,注意,并不会返回被弹出元素的值。
访问队首元素,如例:q.front(),即最早被压入队列的元素。
访问队尾元素,如例:q.back(),即最后被压入队列的元素。
判断队列空,如例:q.empty(),当队列空时,返回true。
访问队列中的元素个数,如例:q.size()
#include 4.2层序介绍
层序遍历就是逐层遍历树结构。
广度优先搜索是一种广泛运用在树或图这类数据结构中,遍历或搜索的算法。 该算法从一个根节点开始,首先访问节点本身。 然后遍历它的相邻节点,其次遍历它的二级邻节点、三级邻节点,以此类推。
当我们在树中进行广度优先搜索时,我们访问的节点的顺序是按照层序遍历顺序的。
4.3层序遍历例子
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if(root == NULL) return{};
queue<TreeNode*> q;
vector<vector<int>> res;
// 根节点进入队列
q.push(root);
while(q.size()){
//一层中含有的节点先用变量保存下来,不然后面有节点加入队列后size()有变化
int layerSize = q.size();
//一层的vector
vector<int> layerRes;
for(int i = 0; i<layerSize; i++){
//取出地一个元素
TreeNode *pNode = q.front();
//删除地一个元素
q.pop();
if(pNode == NULL)
continue;
layerRes.push_back(pNode->val);
//该节点有无左右节点?
if(pNode->left != NULL)
q.push(pNode->left);
if(pNode->right != NULL)
q.push(pNode->right);
}
//一层结束了,该层的vector加入大vector
if(!layerRes.empty()){
res.push_back(layerRes);
}
}
return res;
}
};