Dynamic R-CNN|在训练时动态改变标签分配阈值和SmoothL1损失超参
论文标题:Dynamic R-CNN: Towards High Quality Object Detection via Dynamic Training
论文下载地址:https://arxiv.org/abs/2004.06002
源码下载地址:https://github.com/hkzhang95/DynamicRCN
动机
在传统的二阶段检测器训练过程中,用于分类任务标签分配的IoU阈值是固定的,设置较高的IoU阈值会提高正样本的质量,然而在训练的初始阶段,直接设置较高的IoU阈值会导致正样本数量稀少,不利于训练,因此可以在训练前期设置较低的IoU阈值,保证正样本数量;在训练后期,随着proposal质量的提高,设置较高的IoU阈值,保证正样本质量。
类似地,在回归任务中,Bounding Box的回归目标分布也随着训练过程改变,使用超参确定的SmoothL1损失也不利于模型性能的进一步提高。
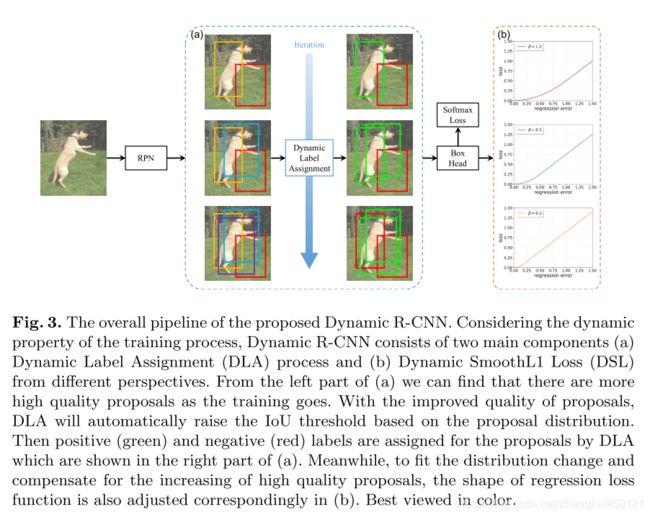
Dynamic R-CNN
作者提出了Dynamic R-CNN,改进了传统二阶段检测器中分类任务的标签分配策略和回归任务的SmoothL1损失。
Dynamic Label Assignment(DLA)
传统的标签分类策略为:
label = { 1 , if max IoU ( b , G ) ≥ T + 0 , if max IoU ( b , G ) < T − − 1 , otherwise \text { label }=\left\{\begin{array}{ll} 1, & \text { if } \max \operatorname{IoU}(b, G) \geq T_{+} \\ 0, & \text { if } \max \operatorname{IoU}(b, G)
设置阈值 T + T_{+} T+和 T − T_{-} T−,Bounding Box和ground truth的IoU大于 T + T_{+} T+,则标记该proposal为正样本;当IoU小于 T − T_{-} T−时,标记该proposal为负样本;否则忽略该proposal。
DLA(动态标签分配)策略如下:
label = { 1 , if max IoU ( b , G ) ≥ T n o w 0 , if max IoU ( b , G ) < T n o w \text { label }=\left\{\begin{array}{ll} 1, & \text { if } \max \operatorname{IoU}(b, G) \geq T_{n o w} \\ 0, & \text { if } \max \operatorname{IoU}(b, G)
T n o w T_{n o w} Tnow表示当前阶段的IoU阈值, T n o w T_{n o w} Tnow的值随着训练过程中proposal质量的提高而改变。在训练过程中,将样本的IoU集合记作 I I I,记录下当前batch中第 K I K_I KI大的IoU值;每进行 C C C次迭代,对 C C C次迭代过程中记录的第 K I K_I KI大的IoU取平均值用来更新 T n o w T_{n o w} Tnow。随着训练的进行,proposal的质量不断提高, T n o w T_{n o w} Tnow的值也不断增大,训练时正样本的质量也在提高。
Dynamic SmoothL1 Loss
传统的SmoothL1损失为:
SmoothL1 ( x , β ) = { 0.5 ∣ x ∣ 2 / β , if ∣ x ∣ < β ∣ x ∣ − 0.5 β , otherwise \text { SmoothL1 }(x, \beta)=\left\{\begin{array}{ll} 0.5|x|^{2} / \beta, & \text { if }|x|<\beta \\ |x|-0.5 \beta, & \text { otherwise } \end{array}\right. SmoothL1 (x,β)={0.5∣x∣2/β,∣x∣−0.5β, if ∣x∣<β otherwise
β \beta β为确定SmoothL1的超参数,在传统二阶段检测器的训练过程中, β \beta β为定值; x x x为回归目标,在回归分支中,回归目标为offset Δ = ( δ x , δ y , δ w , δ h ) \Delta=\left(\delta_{x}, \delta_{y}, \delta_{w}, \delta_{h}\right) Δ=(δx,δy,δw,δh),它们的定义如下:
δ x = ( g x − b x ) / b w , δ y = ( g y − b y ) / b h δ w = log ( g w / b w ) , δ h = log ( g h / b h ) \begin{array}{c} \delta_{x}=\left(g_{x}-b_{x}\right) / b_{w}, \quad \delta_{y}=\left(g_{y}-b_{y}\right) / b_{h} \\ \delta_{w}=\log \left(g_{w} / b_{w}\right), \quad \delta_{h}=\log \left(g_{h} / b_{h}\right) \end{array} δx=(gx−bx)/bw,δy=(gy−by)/bhδw=log(gw/bw),δh=log(gh/bh)
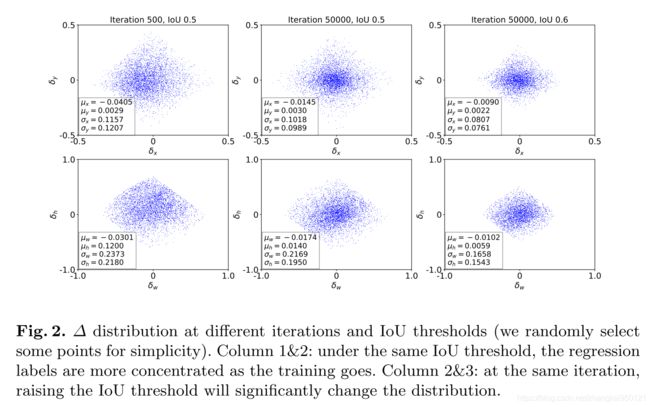
作者认为,随着训练的进行,回归目标的分布发生变化,对比下图中前2栏:
随着训练的进行,回归目标的分布变得更集中,值也更小。
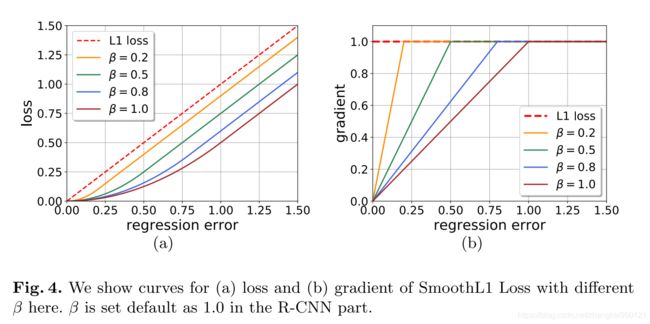
下图为SmoothL1损失中不同的 β \beta β值对损失值和梯度的影响:
作者认为,更小的 β \beta β会使得梯度容易饱和,使得高质量的proposal对网络训练的影响更大。
因此在网络训练过程中,根据回归目标分布的变化,动态地调整SmoothL1损失函数中的 β \beta β值:
D S L ( x , β n o w ) = { 0.5 ∣ x ∣ 2 / β now , if ∣ x ∣ < β now ∣ x ∣ − 0.5 β now , otherwise D S L\left(x, \beta_{n o w}\right)=\left\{\begin{array}{ll} 0.5|x|^{2} / \beta_{\text {now }}, & \text { if }|x|<\beta_{\text {now }} \\ |x|-0.5 \beta_{\text {now }}, & \text { otherwise } \end{array}\right. DSL(x,βnow)={0.5∣x∣2/βnow ,∣x∣−0.5βnow , if ∣x∣<βnow otherwise
对于每个回归目标,每次记录第 K β K_{\beta} Kβ个最小的值,每 C C C次迭代更新一次 β n o w \beta_{now} βnow,取这 C C C次中记录值的中位数。
训练过程中,IoU阈值的变化和 β \beta β的变化示意图如下:
结果
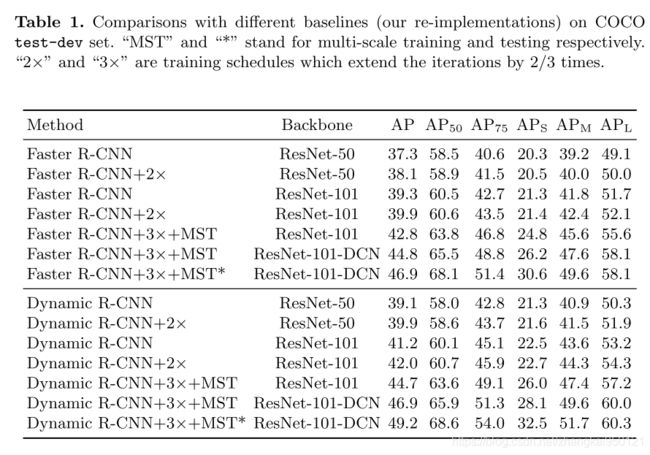
作者使用Backbone为ResNet50的带有FPN的Faster-RCNN作为baseline,加入Dynamic Label Assignment和Dynamic SmoothL1 Loss的性能提升如下表所示:
如果你对计算机视觉中的目标检测、跟踪、分割、轻量化神经网络感兴趣,欢迎关注公众号一起交流~

推荐阅读:
CPN|一个Anchor-free, Two-stage的目标检测器
TIDE|一个通用的目标检测失效分析工具
PIoU Loss|用于提高旋转目标检测器性能的新型损失函数