2020蓝桥杯省赛A组部分赛题

前言

同样，因为题目相近原创审核不通过。

结果填空

试题A 门牌制作

本题总分：5 分
【问题描述】
小蓝要为一条街的住户制作门牌号。这条街一共有2020 位住户，门牌号从1 到2020 编号。小蓝制作门牌的方法是先制作0 到9 这几个数字字符，最后根据需要将字符粘贴到门牌上，例如门牌1017 需要依次粘贴字符1、0、1、7，即需要1 个字符0，2 个字符1，1 个字符7。请问要制作所有的1 到2020 号门牌，总共需要多少个字符2？

#include 
using namespace std;

int main() {
	int x, num = 0;
	for (int i = 1; i <= 2020; i++) {
		x = i;
		while(x > 0) {
			if (x % 10 == 2)
				num++;
			x /= 10;
		}
	}
	cout << num << endl;
}

答案：624

试题B: 既约分数

本题总分：5 分
【问题描述】
如果一个分数的分子和分母的最大公约数是1，这个分数称为既约分数。例如，3/4 , 5/2 , 1/8 , 7/1都是既约分数。请问，有多少个既约分数，分子和分母都是1 到2020 之间的整数（包括1和2020）？

#include 
using namespace std;

int gcd(int a, int b) {
	if (a % b == 0)
		return b;
	return gcd(b, a % b);
} 

int main() {
	long num = 0;
	for (int i = 1; i <= 2020; i++) {
		for (int j = 1; j <= 2020; j++) {
			if (gcd(i, j) == 1)
				num++;	
		}
	}
	cout << num << endl;
}

【答案提交】
答案：2481215

试题C 蛇形填数

10分
【问题描述】
如下图所示，小明用从1 开始的正整数“蛇形”填充无限大的矩阵。

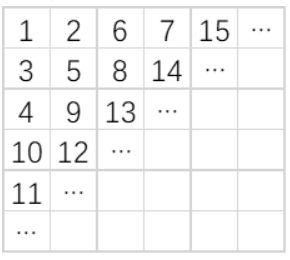
容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20 行第20 列的数是多少？

#include 
using namespace std;

int main() {
	int a[100][100];
	int x, y, cnt = 1;
	for (int i = 1; i <= 40; i++) {
		if (i % 2 == 1) {
			// 左下 -> 右上
			for (x = i, y = 1; x >= 1 && y <= i; x--, y++)
				a[x][y] = cnt++; 
		} else {
			// 右上 -> 左下
			for (x = 1, y = i; x <= i && y >= 1; x++, y--)
				a[x][y] = cnt++; 
		}
	}
	cout << a[20][20] << endl;
}

答案：761

试题D: 七段码

本题总分：10 分

【问题描述】
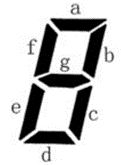
小蓝要用七段码数码管来表示一种特殊的文字。
上图给出了七段码数码管的一个图示，数码管中一共有7 段可以发光的二极管，分别标记为a, b, c, d, e, f, g。小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？

题目考察并查集。
题解来源： https://blog.csdn.net/qq_45530271/article/details/109189978
很感谢这位博主让我学会了怎么用并查集和回溯法解决这道题。

#include 
using namespace std;

const int N = 10;
int use[N], ans = 0, e[N][N], parent[N];

void init() {
	/*	
		连边建图，e[i][j]==1表示i和j相邻
		a b c d e f g
		1 2 3 4 5 6 7
	*/
	e[1][2] = e[1][6] = 1;
	e[2][1] = e[2][3] = e[2][7] = 1;
	e[3][2] = e[3][4] = e[3][7] = 1;
	e[4][3] = e[4][5] = 1;
	e[5][4] = e[5][6] = e[5][7] = 1;
	e[6][1] = e[6][5] = e[6][7] = 1;
	e[7][2] = e[7][3] = e[7][5] = e[7][6] = 1;
}

int find(int u) {
	if (u != parent[u])
		parent[u] = find(parent[u]);
	return parent[u];
}

void dfs(int d) {
	if (d > 7) {
		for (int i = 1; i <= 7; i++)
			parent[i] = i;
		for (int i = 1; i <= 7; i++)
			for (int j = 1; j <= 7; j++)
				if (e[i][j] && use[i] && use[j]) {
					int pi = find(i), pj = find(j);
					if (pi != pj)
						// 如果不在同一个集合, 合并 
						parent[pi] = pj;
				}
		int k = 0;
		for (int i = 1; i <= 7; i++)
			if (use[i] && parent[i] == i)
				k++;
		// 如果所有亮灯都属于同一个集合 
		if (k == 1)
			ans++;
		return;
	}
	// 打开d这个灯 
	use[d] = 1;
	// 摸索下一个灯 
	dfs(d + 1);
	// 关闭 d这个灯 
	use[d] = 0;
	dfs(d + 1);
}

int main() {
	init();
	dfs(1);
	cout << ans << endl;
}

【答案提交】
80

这里顺带提一嘴这个并查集的查找函数的写法。

int find(int u) {
	if (u != parent(u))
		parent[u] = find(parent[u]);
	return parent[u];
}

这里 parent[u] 是有必要的， 因为可能到时候虽然是union了, 但是还是有些数据跟不上。下面举个例子。

void union(int x, int y) {
	int px = find(x);
	int py = find(y);
	if (px != py) {
		parent[px] = py;
	}
}

1 -> 2 -> 3 (假设 child -> parent, 即 2 是 1 的 双亲，3 是 2 的双亲),
parent[] = {x, 2, 3, 3, …},
这里我们union(3, 4), 此时
parent[] = {x, 2, 3, 4, 4, …},
但是我们为了每次find的时候效率更高，因为并查集只是相判断一下两个元素是否在同个集合中而已， 所以我们会让
parent[] = {x, 4, 4, 4, 4, …},
因此我们在find的时候， 当 u != parent[u] 的时候，还是会把 find(parent[u]) 的结果传给 parent[u] , 即代码中的

parent[u] = find(parent[u]);

其实上面的代码可以再写得更像并查集模板一点:

#include 
using namespace std;

const int N = 10;
int use[N], ans = 0, e[N][N], parent[N];

void init() {
	/*	
		连边建图，e[i][j]==1表示i和j相邻
		a b c d e f g
		1 2 3 4 5 6 7
	*/
	e[1][2] = e[1][6] = 1;
	e[2][1] = e[2][3] = e[2][7] = 1;
	e[3][2] = e[3][4] = e[3][7] = 1;
	e[4][3] = e[4][5] = 1;
	e[5][4] = e[5][6] = e[5][7] = 1;
	e[6][1] = e[6][5] = e[6][7] = 1;
	e[7][2] = e[7][3] = e[7][5] = e[7][6] = 1;
}

int find(int u) {
	if (u != parent[u])
		parent[u] = find(parent[u]);
	return parent[u];
}

void tryUnion(int x, int y) {
	int px = find(x), py = find(y);
	if (px != py) {
		parent[px] = py;
	}
}

void dfs(int d) {
	// 终止条件 
	if (d > 7) {
		for (int i = 1; i <= 7; i++)
			parent[i] = i;
		for (int i = 1; i <= 7; i++)
			for (int j = 1; j <= 7; j++)
				if (e[i][j] && use[i] && use[j])
					tryUnion(i, j);
		int setNum = 0;
		for (int i = 1; i <= 7; i++)
			if (use[i] && parent[i] == i)
				setNum++;
		if (setNum == 1)
			ans++;
		return;
	}
	use[d] = 1;
	dfs(d + 1);
	use[d] = 0;
	dfs(d + 1);
}

int main() {
	init();
	dfs(1);
	cout << ans << endl;
}

试题E: 平面分割

本题总分：15 分
【问题描述】
20 个圆和20 条直线最多能把平面分成多少个部分？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

程序设计题

试题F 成绩统计

15分
【问题描述】
小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是
一个 0 到 100 的整数。
如果得分至少是 60 分，则称为及格。如果得分至少为 85 分，则称为优秀。
请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整
数。

【输入格式】
输入的第一行包含一个整数 n，表示考试人数。
接下来 n 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。

【输出格式】
输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分
四舍五入保留整数。

【样例输入】

7
80
92
56
74
88
100
0

71%
43%

【评测用例规模与约定】
对于50% 的评测用例， 1 ≤ n ≤ 100。
对于所有评测用例，1 ≤ n ≤10000。

#include 
using namespace std;

int main() {
	int x, jige = 0, youxiu = 0, n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> x; 
		if (x >= 60)
			jige++;
		if (x >= 85)
			youxiu++;
	}
	cout << int(jige * 1.0 / n * 100 + 0.5) << "%" << endl;
	cout << int(youxiu * 1.0 / n * 100 + 0.5) << "%" << endl;
}

试题G 回文日期

20分
【问题描述】
2020 年春节期间，有一个特殊的日期引起了大家的注意：2020年2月2日。因为如果将这个日期按“yyyymmdd” 的格式写成一个8 位数是20200202，
恰好是一个回文数。我们称这样的日期是回文日期。
有人表示20200202 是“千年一遇” 的特殊日子。对此小明很不认同，因为不到2年之后就是下一个回文日期：20211202 即2021年12月2日。
也有人表示20200202 并不仅仅是一个回文日期，还是一个ABABBABA型的回文日期。对此小明也不认同，因为大约100 年后就能遇到下一个ABABBABA 型的回文日期：21211212 即2121 年12 月12 日。算不上“千年一遇”，顶多算“千年两遇”。
给定一个8 位数的日期，请你计算该日期之后下一个回文日期和下一个ABABBABA型的回文日期各是哪一天。

【输入格式】
输入包含一个八位整数N，表示日期。

【输出格式】
输出两行，每行1 个八位数。第一行表示下一个回文日期，第二行表示下
一个ABABBABA 型的回文日期。

【样例输入】

20200202

【样例输出】

20211202
21211212

【评测用例规模与约定】
对于所有评测用例，10000101 ≤ N ≤ 89991231，保证N 是一个合法日期的8位数表示。

题解来自：第十一届蓝桥杯 ——回文日期 , 强烈建议大家看一下他的解题思路，原作者写的很详细。

#include 
#include 
using namespace std;

int days[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

bool isLeap(int year) {
	return year % 400 == 0 || year % 4 == 0 && year % 100 != 0;
}

int getDay(int year, int month) {
	if (month == 2)
		return days[2] + isLeap(year);
	return days[month];
}

int main() {
	int n;
	cin >> n;
	
	string ans1, ans2;
	bool flag1 = false, flag2 = false;
	for (int i = n / 10000; i <= 9999; i++) {
		string a = to_string(i);
		string b = a;
		reverse(b.begin(), b.end());
		if (a + b == to_string(n))
			continue;
		
		// 判断月份日期是否合法	
		int month = stoi(b.substr(0, 2));
		int day = stoi(b.substr(2, 2));
		if (month < 1 || month > 12)
			continue;
		if (day < 1 || day > getDay(i, month))
			continue;
			
		string s1 = a.substr(0, 2);
		string s2 = a.substr(2, 2);
		if (!flag1) {
			ans1 = a + b;
			flag1 = true;
		}
		if (!flag2 && s1 == s2 && s1[0] != s1[1]) {
			ans2 = a + b;
			flag2 = true;
		}
		
		if (flag1 && flag2)
			break;
	}
	cout << ans1 << endl;
	cout << ans2 << endl;
}

虽然个人觉得还能这样子:

#include 
#include 
using namespace std;

int days[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

bool isLeap(int year) {
	return year % 400 == 0 || year % 4 == 0 && year % 100 != 0; 
}

int getDay(int year, int month) {
	if (month == 2)
		return days[month] + isLeap(year);
	return days[month];	
}

int main()  {
	int n;
	cin >> n;
	
	string ans1, ans2;
	bool flag1 = false, flag2 = false;
	
	for (int i = n / 10000 + 1; i <= 9999; i++) {
		string a = to_string(i);
		string b = a;
		reverse(b.begin(), b.end());
//		if (a + b == to_string(n))
//			continue;
			
		int month = stoi(b.substr(0, 2));
		int day = stoi(b.substr(2, 2));
		if (month < 1 || month > 12)
			continue;
		if (day < 1 || day > getDay(i, month))	
			continue;
		
		string s1 = a.substr(0, 2);
		string s2 = a.substr(2, 2);
		
		if (!flag1) {
			ans1 = a + b;
			flag1 = true;
		}
		
		if (!flag2 && s1 == s2 && s1[0] != s1[1]) {
			ans2 = a + b;
			flag2 = true;
		}
		
		if (flag1 && flag2)
			break;
	}
	cout << ans1 << endl;
	cout << ans2 << endl;
}

试题H: 子串分值

【输入格式】
输入一行包含一个由小写字母组成的字符串S。

【输出格式】
输出一个整数表示答案。

【样例输入】

ababc

【样例输出】

28

【样例说明】
子串f值：

a     1
ab    2
aba   1
abab  0
ababc 1
 b    1
 ba   2
 bab  1
 babc 2
  a   1
  ab  2
  abc 3
   b  1
   bc 2
    c 1

【评测用例规模与约定】
对于20% 的评测用例，1 ≤ n ≤ 10；
对于40% 的评测用例，1 ≤ n ≤ 100；
对于50% 的评测用例，1 ≤ n ≤ 1000；
对于60% 的评测用例，1 ≤ n ≤ 10000；
对于所有评测用例，1 ≤ n ≤ 100000。

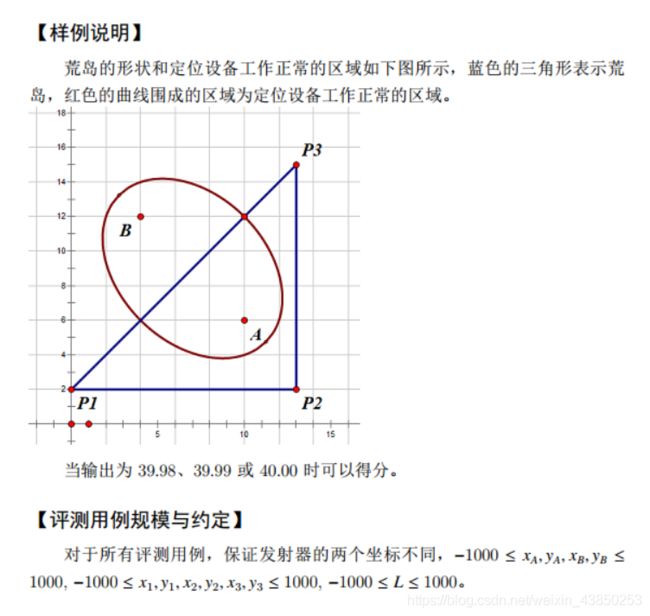
荒岛探测

25分

【输出格式】
输出一行，包含一个实数，四舍五入保留2位小数，表示答案。
考虑到计算中的误差，只要你的输出与参考输出相差不超过0.01即可得分。

【样例输入】

10 6 4 12 12
0 2 13 2 13 15

【样例输出】

39.99

【样例说明】
当输出为39.98、39.99或40.00时可以得分。

子串排序

【问题描述】
小蓝最近学习了一些排序算法，其中冒泡排序让他印象深刻。在冒泡排序中，每次只能交换相邻的两个元素。小蓝发现，如果对一个字符串中的字符排序，只允许交换相邻的两个字符，则在所有可能的排序方案中，冒泡排序的总交换次数是最少的。
例如，对于字符串 lan 排序，只需要 1 次交换。对于字符串 qiao 排序，
总共需要 4 次交换。小蓝找到了很多字符串试图排序，他恰巧碰到一个字符串，需要 V 次交换，可是他忘了把这个字符串记下来，现在找不到了。
请帮助小蓝找一个只包含小写英文字母且没有字母重复出现的字符串，对该串的字符排序，正好需要 V 次交换。如果可能找到多个，请告诉小蓝最短的那个。如果最短的仍然有多个，请告诉小蓝字典序最小的那个。请注意字符串中可以包含相同的字符。

【输入格式】
输入的第一行包含一个整数V，小蓝的幸运数字。

【输出格式】
题面要求的一行字符串。

【样例输入】

4

【样例输出】

bbaa

【样例输入】

100

【样例输出】

jihgfeeddccbbaa

【评测用例规模与约定】
对于 30% 的评测用例， 1 ≤ V ≤ 20。
对于 50% 的评测用例， 1 ≤ V ≤ 100。
对于所有评测用例， 1 ≤ V ≤ 10000。