朝题夕解——动态规划之整数划分模型
映射思想解决整数划分类DP问题
-
- 整数划分类DP问题的常规解决思想
- 实战练习
-
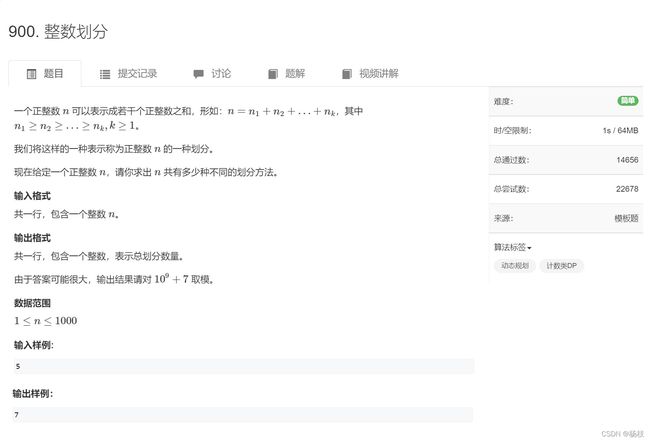
- 题目描述
- 解题报告
- 参考代码(C++版本)
- 推导演练
-
- 题目描述
- 解题报告
- 参考代码(C++版本)
- 小总结
整数划分类DP问题的常规解决思想
| 整数划分类型的DP有时候也被叫做计数类DP。称呼不同,都是它啦~。我这篇博客的话,主要想记录一下在这种DP问中经常会使用的映射思想。并不是总结怎么拿捏这种类型的DP |
| 求学于acwing门下的师兄师姐们看到DP问题,心中大抵都在对状态表示和状态计算打小算盘了吧。这里先借用一下师兄的总结,系统的看一下DP思考方向。 |
- 我对"状态表示"的理解
| 状态表示的常规玩法是题目问什么,咱们就定义出一个集合来表示这个问题。 因为这个集合数组最终是要存放一个数据,这就是集合的属性。 比如题目问的意思是N个物品,容积为V的背包最多可以获得的最大价值是多少。那么这个集合数组就就可以定义为 f[i][j],属性就选最大值。它们表示的意思是i个物品下,容积为j时,可以获得的最大值。 |
- 我对"状态计算"的理解
| 状态计算对应的是对所构建的集合进行不重不漏的划分,划分的依据大多是题目中的最后一个不同点。 |
实战练习
题目描述
解题报告
状态表示:
集合: f ( i , j ) f(i,j) f(i,j)表示使用 j j j个数能够凑成总和为 i i i的方案的集合
属性: f [ i , j ] f[i,j] f[i,j]中存放的是这些方案的数量
状态计算:
题目中提到
一个正整数 n可以表示成若干个正整数之和,咱们的数学常识中可以知道,正整数是大于等于1的数。
题目中规定了 n 1 > = n 2 > = . . . > = n k , k > = 1 n_1>= n_2 >= ...>=n_k,k>=1 n1>=n2>=...>=nk,k>=1。1这个数就可以选为最后一个不同点。为什么这么说了,一个方案,要么最后不得不需要一个1来调和,要么直接就可以不需要1的。
因此就可以将j个数中的最小值是否是1选为不同点。
对于最小值是1的情况:
使用 j j j个数凑出总和 i i i。这 j j j个数的最小值为1,那么去掉一个1,则状态状态转移方程可以表示为:
f [ i , j ] f[i,j] f[i,j] = f [ i − 1 , j − 1 ] f[i-1,j-1] f[i−1,j−1]。
最小值不是1的情况:
使用
映射的思想进行处理
使用 j j j个数凑出总和 i i i。这 j j j个数的最小值不为1,那么将这个 j j j个数都去掉一个1,此时在方案的数量不发生改变的情况下,变成了是最小值是1的情况。
f [ i , j ] f[i,j] f[i,j] = f [ i − j , j ] f[i-j,j] f[i−j,j]
通过这种方式,成功的将集合不重不漏的划分出来了。将两种集合划分的情况相加,就是可以得到的全部方案的数量
f [ i , j ] f[i,j] f[i,j] = f [ i − 1 , j ] f[i-1,j] f[i−1,j] + f [ i − j , j ] f[i-j,j] f[i−j,j]
将上面的分析过程进行归纳,就可以得到如下这张清晰的DP分析图

具体落实到代码上,就是如下的样子了。
参考代码(C++版本)
#include
using namespace std;
const int N = 1010, MOD = 1e9+7;
int f[N][N];//集合:f(i,j)表示使用j个数能够凑成总和为i的方案的集合
int n;
int main()
{
scanf("%d",&n);
f[0][0] = 1;
for(int i = 1; i <= n;i++)
for(int j = 1; j <= i;j++)
{
f[i][j] += (f[i-1][j-1]+f[i-j][j])%MOD;
}
// 最后统计出所有得到的总和为n的方案数
int res = 0;
for(int i = 1;i <= n;i++) res = (res+f[n][i])%MOD;
printf("%d\n",res);
return 0;
}
推导演练
题目描述
原题传送门
解题报告
这道题和上一题相比,就是换汤不换药了。唯一的区别是这一题中最小值可以为0。
状态表示:
集合 f ( i , j ) f(i,j) f(i,j)表示总数为 i i i,且划分个数为j的方案的集合
集合的属性是Count
状态计算:
情况一:使用 j j j个数凑成 i i i。这 j j j个数的最小值为0的集合,那么去掉一个0,则状态转移方程为:
f [ i , j ] f[i,j] f[i,j] = f [ i , j − 1 ] f[i,j-1] f[i,j−1]。
情况二:使用映射的思想处理最小值不是0的情况。
使用 j j j个数凑成 i i i。这 j j j个数的最小值不为0的集合,那么将这个j个数都去掉一个1,此时在方案数的总数量不发生改变的情况下,变成咱们熟悉的情况一
f [ i , j ] f[i,j] f[i,j] = f [ i − j , j ] f[i-j,j] f[i−j,j]
将两种集合划分的情况相加,就是可以得到的全部方案的数量
f [ i , j ] f[i,j] f[i,j] = f [ i , j − 1 ] f[i,j-1] f[i,j−1] + f [ i − j , j ] f[i-j,j] f[i−j,j]
同样的,可以得到如下的DP分析图

结合DP分析图,逐渐将代码落实
参考代码(C++版本)
#include
#include
const int N = 15;
int main()
{
int t;
scanf("%d",&t);
//输入t组测试数据
while(t--)
{
//查克拉能量为 M,他影分身的个数最多为 N
int m,n;
scanf("%d %d",&m,&n);
int f[N][N] = {0};
//开始DP之前,思考边界问题
f[0][0] = 1;//0查克拉造0个影分身是一种方案
//这里容易出错,结合着对集合的定义和题意进行理解
for(int i = 0;i <= m;i++)
for(int j = 1; j <= n;j++)
{
//两种集合划分的情况
f[i][j] += f[i][j-1];
if(i >= j) f[i][j] += f[i-j][j];
}
//输出结果
printf("%d\n",f[m][n]);
}
return 0;
}
小总结
状态表示和确定属性比较容易,怎么将集合化整为零的状态计算比较棘手,只是这里处理好,一道DP问题也就差不多可以解决了。本篇也主要是想总结用于状态计算中的一个小技巧——映射。 |