作者：韩信子@ShowMeAI
教程地址：http://www.showmeai.tech/tutorials/34
本文地址：http://www.showmeai.tech/article-detail/197
声明：版权所有，转载请联系平台与作者并注明出处

引言

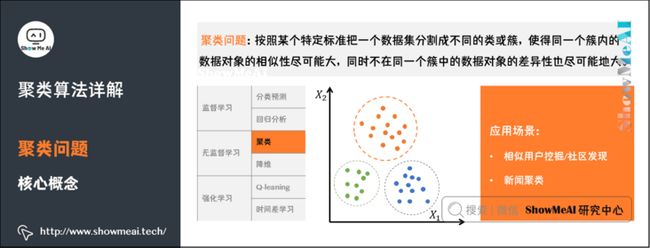
聚类（Clustering）是最常见的无监督学习算法，它指的是按照某个特定标准（如距离）把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

聚类算法在很多场景下都有应用，例如新闻自动分组，用户分群，图像分割等等。很多时候，无监督的聚类算法，得到的聚类结果还可以作为特征在后续监督学习中应用，提升整体效果。本篇内容ShowMeAI带大家一起来学习一下聚类算法。

（本篇聚类算法部分内容涉及到机器学习基础知识，没有先序知识储备的宝宝可以查看ShowMeAI的文章图解机器学习 | 机器学习基础知识。

1.聚类问题

1）聚类问题与核心概念

俗话说人以类聚物以群分，聚类算法做的事情，就是对无标签的数据，基于数据分布进行分群分组，使得相似的数据尽量落在同一个簇内。

我们先对比区分一下聚类和分类：

聚类是一种无监督学习，而分类是一种有监督的学习。
聚类只需要人工指定相似度的标准和类别数就可以，而分类需要从训练集学习分类的方法。

2）聚类算法用途

聚类算法应用非常广泛。在面对未知的世界时，先分类，再逐个研究，是人类探索未知世界的一个基本方法。聚类算法可以应用于探索性数据挖掘、统计分析、生物信息学、数据压缩、计算机图像识别、医学影像分析等，在商业领域可以用来做市场研究、商品归类，在社会科学领域可以用来做犯罪区域分析等等。

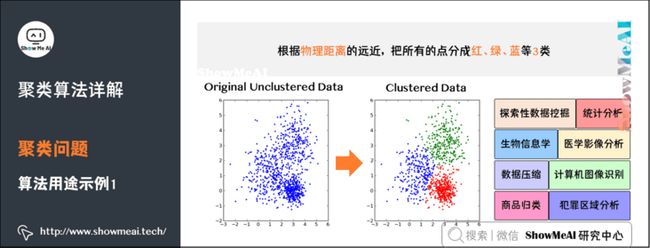
下图中有一些样本点，我们根据物理距离的远近，把所有的点分成3类。你只需要告诉算法这些信息，算法就可以按照你的要求完成聚类：

分类数量为3；
分类标准是物理距离；
分好的类分别用红、绿、蓝表示。

实际上，除了物理距离，现实生活中任何你能想到、计算机可以通过运算和逻辑进行判断的规则，都可以作为分类标准。

下面我们用图像压缩作为例子来解释一下。最左边是一张彩色照片，大小约1Mb，通过压缩可以把它变成几十到几百Kb，这就是压缩软件的实现过程。那么压缩软件的实现原理是什么呢？其中一种就是聚类算法。

从原始图片到压缩存储的过程如下图所示：

聚类算法同样可以用于图像分割。图像中每一个像素点是一个3维向量，对应 [R, G, B] 像素值。给定聚类中类别个数K，算法用K个不同的颜色来表示原来的图像，每个像素点用K个颜色中一个表示。具体如下：

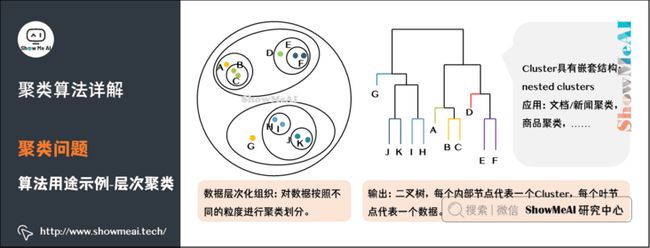
对于文档、新闻、商品而言，很多时候我们会使用嵌套的归类方法，这是一种层次化聚类：

3）主流聚类算法

我们先对聚类算法做个了解，主流的聚类算法可以分成两类：划分聚类（Partitioning Clustering）和层次聚类（Hierarchical Clustering）。他们的主要区别如图中所示：

划分聚类算法会给出一系列扁平结构的簇（分开的几个类），它们之间没有任何显式的结构来表明彼此的关联性。

常见算法有 K-Means/K-Medoids、Gaussian Mixture Model （高斯混合模型）、Spectral Clustering（谱聚类）、Centroid-based Clustering等。

层次聚类会输出一个具有层次结构的簇集合，因此能够比划分聚类输出的无结构簇集合提供更丰富的信息。层次聚类可以认为是是嵌套的划分聚类。

常见算法有 Single-linkage、Complete-linkage、Connectivity-based Clustering等。

这两类算法在聚类过程中用到的具体算法不一样，后文我们会重点展开讲一下K-Means算法、Single-linkage算法和Complete-linkage算法。

2.K-Means聚类算法

K-Means算法是聚类算法中一个非常基础的算法，同时应用又非常广泛，下面ShowMeAI给大家展开讲解算法原理。

1）K-Means算法核心概念

我们提到了聚类算法要把n个数据点按照分布分成k类（很多算法的k是人为提前设定的）。我们希望通过聚类算法得到k个中心点，以及每个数据点属于哪个中心点的划分。

中心点可以通过迭代算法来找到，满足条件：所有的数据点到聚类中心的距离之和是最小的。
中心点确定后，每个数据点属于离它最近的中心点。

在进入「如何寻找中心点」这个核心问题之前，我们先解决几个小问题：

Q1：数据点到中心点的距离如何计算？

我们一般选择几何距离，就是L2距离的平方。

Q2：中心点是否唯一，或者说，是不是存在全局最优解？

对于多个中心点的情况，全局最优是一个相当难的问题。理论上存在一个全局最优解，但是不一定能找到。既然全局最优解不好找，那我们退而求其次，看能不能找到局部最优解。

Q3：聚类结果如何表示？

采用空间分割的方式：将空间分割成多个多边形，每个多边形对应一个cluster中心。

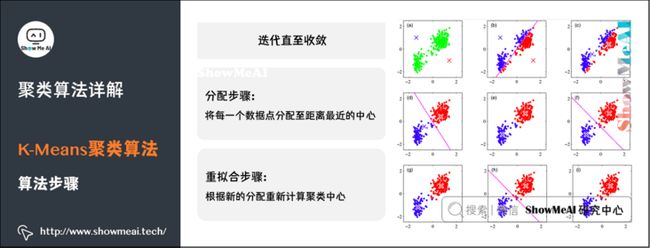
2）K-Means算法步骤

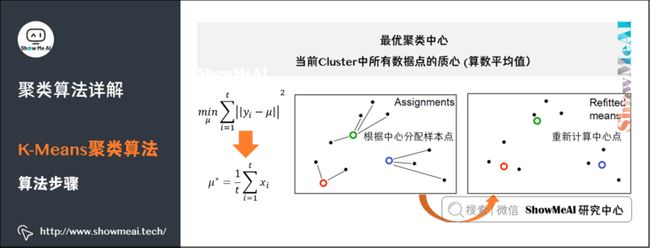
K-Means采用EM算法迭代确定中心点。流程分两步：

① 更新中心点：初始化的时候以随机取点作为起始点；迭代过程中，取同一类的所有数据点的重心（或质心）作为新中心点。
② 分配数据点：把所有的数据点分配到离它最近的中心点。

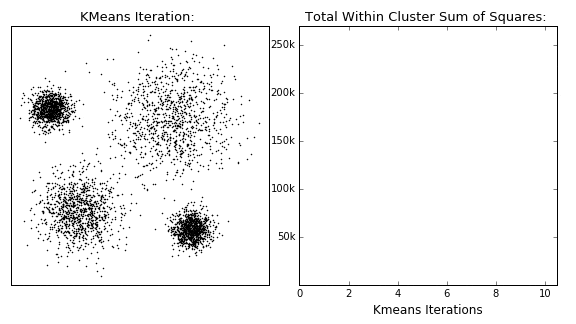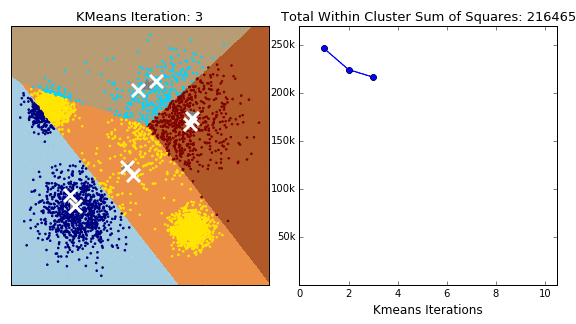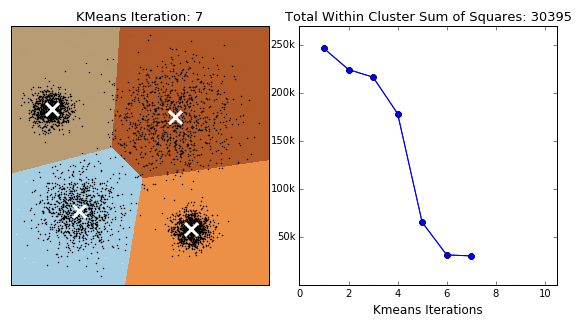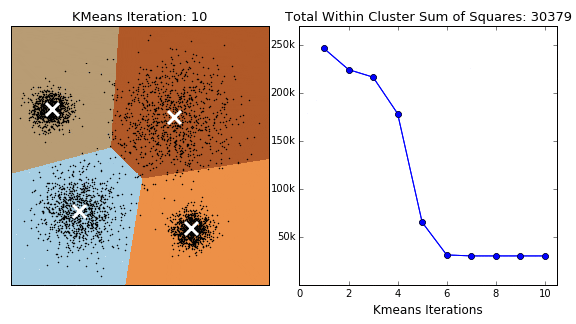
重复上面的两个步骤，一直到中心点不再改变为止。过程如图所示：

左侧Assignments：一开始随机选取三个点，作为三个类的中心，基于其它点和这三个中心点的距离分配簇；每一类重新计算和分配中心。
右侧Refitted Means：根据新的中心点，重新分配所有的数据点（原来属于绿色中心点的1个点，此次迭代后变成属于红色中心点了）。

下图的示例展示了K-Means动态迭代收敛的过程：

图（a）上有一群散落的点，我们设定簇数K=2。
图（b）为随机找2个点作为中心初始化后，第一次分类的结果。
- 可以看到，红蓝分界线在这群点的中央穿过。这显然有问题，不过没关系，算法继续往下走。对红蓝两类分别计算它们的中心。
图（c）可以看到，一个落在左下方这一团里，另一个落在右上方那一团里。以新的中心点进行第二次分类。
图（d）的分界线就基本是已经可以把两团分开了。
图（f）、（g）显示后续重复计算你「中心点-分类数据点」的过程已经收敛，数据点分配基本不动了，聚类完成。

下方的动图能更清晰地展示这个过程：

3.K-Means缺点与改进

1）K-Means算法缺点

K-Means算法简单易用，它有什么缺点呢？我们将K-Means算法的一些缺点总结如下：

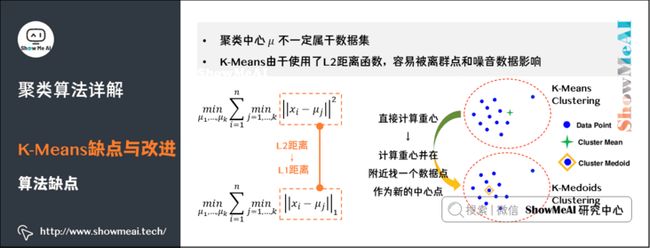
缺点1：中心点是所有同一类数据点的质心，所以聚类中心点可能不属于数据集的样本点。
缺点2：计算距离时我们用的是L2距离的平方。对离群点很敏感，噪声（Noisy Data）和离群点（Outlier）会把中心点拉偏，甚至改变分割线的位置。

2）K-Medoids算法

针对K-Means算法的缺点改进得到了K-Medoids算法：

（1）限制聚类中心点必须来自数据点。

求中心点的计算方法，由原来的直接计算重心，变成计算完重心后，在重心附近找一个数据点作为新的中心点。
K-Medoids重拟合步骤比直接求平均的K-Means要复杂一些。

（2）为避免平方计算对离群点的敏感，把平方变成绝对值。

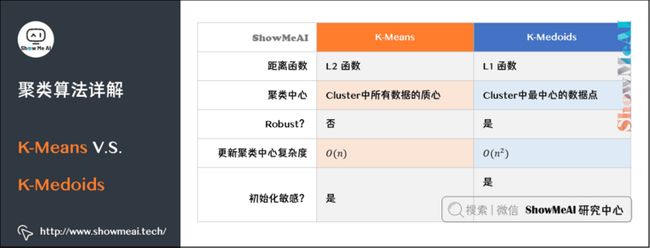
总结来说，K-Medoids算法的迭代过程与K-Means是一致的，不同点如下所示：

起始点不是随机点，而是任意选择数据集中的点。
距离使用L1距离，而不是L2距离。
新的中心点，也不是同类所有点的重心，而是同一类别所有数据点中，离其它点最近的点。
复杂度方面，相比于K-Means的 \(O(n)\) ，K-Medoids更新中心点的复杂度 \(O(n^2)\) 要更高一些。

下图是K-Means和K-Medoids两个算法的一个系统对比：

4.层次聚类算法

相比于K-Means这类划分聚类，我们有另外一类层次化聚类算法。

1）层次聚类vs划分聚类

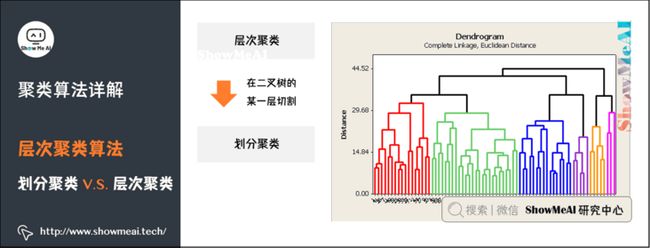
划分聚类得到的是划分清晰的几个类，而层次聚类最后得到的是一个树状层次化结构。

从层次化聚类转换为划分聚类很简单，在层次化聚类的某一层进行切割，就得到1个划分聚类。如下图所示：

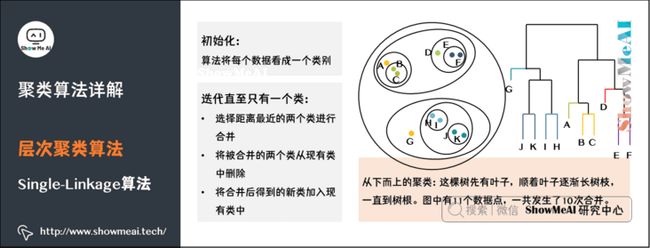
2）Single-Linkage 算法

接下来我们介绍一个层次聚类中的Single-Linkage算法。这个算法是构造一棵二叉树，用叶节点代表数据，而二叉树的每一个内部节点代表一个聚类。如图所示：

这是一个从下而上的聚类。这棵树是先有叶子，顺着叶子逐渐长树枝，树枝越长越大一直到树根。

如果叶子很多，这个生长过程需要合并的类就会很多。图中有11个数据点，一共发生了10次合并。

3）Complete-Linkage算法

与Single-Linkage算法相似，Complete-Linkage的迭代思路是一样的，不同的是在合并类时，Single-Linkage是用两个类中距离最小的两个点作为类之间的距离，而Complete-Linkage恰恰相反，用距离最远的两个数据点之间的距离作为这两个类之间的距离。

这两种计算方法各有利弊。总的来说，层次聚类的计算复杂度是 \(O(n^3)\) 级别，算是很高的了。可以用优先队列的数据结构对算法加速，加速后能减低到 \(O(n^{2} \log{n} )\) 的级别。

5.DB-SCAN算法

1）DB-SCAN算法

在前面的内容中我们介绍了划分聚类和层次聚类的算法，接下来我们学习另外一个聚类算法：DB-SCAN算法。

DB-SCAN是一个基于密度的聚类。如下图中这样不规则形态的点，如果用K-Means，效果不会很好。而通过DB-SCAN就可以很好地把在同一密度区域的点聚在一类中。

2）DB-SCAN算法的关键概念

核心对象（Core Object），也就是密度达到一定程度的点。

若 \(x_j\) 的 \(\in -\) 邻域至少包含MinPts个样本，即 \(|N_\in (x_j )|≥MinPts\) ，则 \(x_j\) 是一个核心对象。

密度直达（directly density-reachable），密度可达（density-reachable）：核心对象之间可以是密度直达或者密度可达。

若 \(x_i\) 位于 \(x_j\) 的 \(\in -\) 邻域中，且 \(x_j\) 是核心对象，则称 \(x_j\) 由 \(x_j\) 密度直达。
对 \(x_i\) 与 \(x_j\) ，若存在样本序列 \(p_1,p_2, \dots, p_n\) ，其中 \(p_1=x_i\) ， \(p_n=x_j\) 且 \(p_i+1\) 由 \(p_i\) 密度直达，则称 \(x_j\) 由 \(x_i\) 密度可达。

密度相连（density-connected）：所有密度可达的核心点就构成密度相连。

对 \(x_i\) 与 \(x_j\) ，若存在 \(x_k\) 使得 \(x_i\) 与 \(x_j\) ，均由 \(x_k\) 密度可达，则称 \(x_i\) 与 \(x_j\) 密度相连。

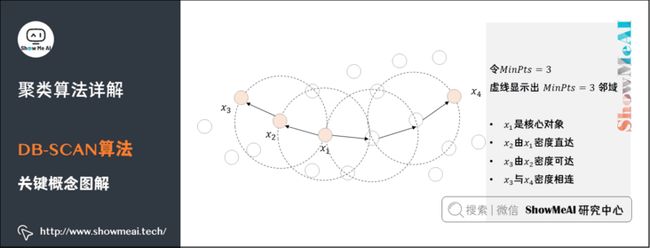
我们通过下图深入理解一下刚才提到的几个基本概念。

先假设要求的最小点密度MinPts是3。

在一个半径范围内， \(x_1\) 这个点周围的点数是5，超过了阈值3，所以 \(x_1\) 是一个核心对象。同样， \(x_2\) 、 \(x_3\) 和 \(x_4\) 也是核心对象。
\(x_1\) 与 \(x_2\) 处于一个邻域，所以二者是密度直达的关系，而 \(x_3\) 与 \(x_2\) 也是密度直达的关系，通过 \(x_2\) ， \(x_1\) 与 \(x_3\) 是密度可达的关系。
\(x_3\) 与 \(x_4\) 通过多个核心对象实现密度相连。

3）DB-SCAN算法伪代码

这个过程用直白的语言描述就是：

对于一个数据集，先规定最少点密度MinPts和半径范围。
先找出核心对象：如果在半径范围内点密度大于MinPts，则这个点是核心对象。把所有的核心对象放到一个集合中。
从这个核心对象集合中，随机找一个核心对象，判断其它的数据点与它是否密度直达，如果是，则归入聚类簇中。
继续判断其它点与聚类簇中的点是否密度直达，直到把所有的点都检查完毕，这时候归入聚类簇中的所有点是一个密度聚类。

更多无监督学习的算法模型总结可以查看ShowMeAI的文章 AI知识技能速查 | 机器学习-无监督学习。

视频教程

可以点击 B站查看视频的【双语字幕】版本

https://www.bilibili.com/vide...

【双语字幕+资料下载】MIT 6.036 | 机器学习导论(2020·完整版)

https://www.bilibili.com/video/BV1y44y187wN?p=13

图解机器学习 | 聚类算法详解

引言