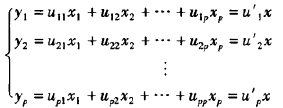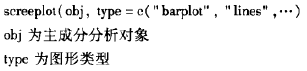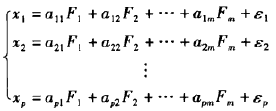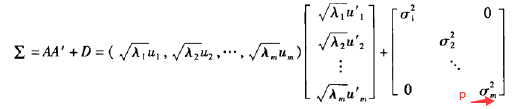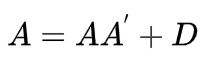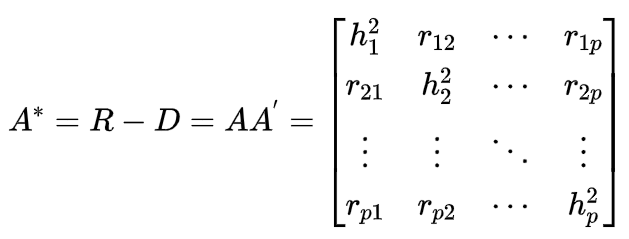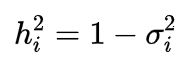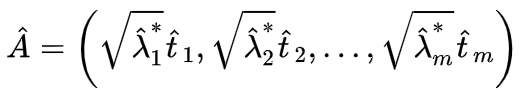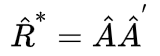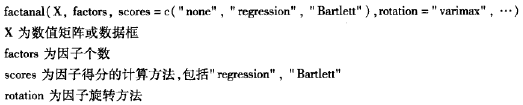r语言主成分分析_多元统计分析与R语言建模之主成分分析和因子分析
侵权声明：
本篇文章是查阅各种网络技术博客撰写的，仅供学习使用，如有侵权立即删除。
主成分分析——将多指标转化为少数几个指标
简单地说，就是将一系列具有相关性的指标重新组合成数量更少且互不相关的指标。用较少且相互独立的指标取解释数据的大部分变异。
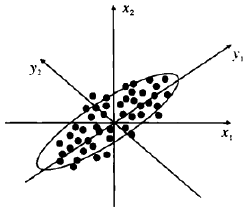
大家应该经常看见这幅图：
下面具体解释一下吧。
目前有两个变量x1和x2，从它们形成的散点图可以看出x1和x2呈现线性关系，也就是说x1和x2之间有较大的相关性。于是试图将x1和x2进行重新组合，也就是进行线性变换形成y1和y2。那么y1和y2均是x1和x2的线性组合，只是y1和y2不相关罢了。如果将x1、x2和y1、y2画在一个坐标系下，就是图中所示的情况了。从图中可以看出，散点主要散布在在y1轴。那如果舍去y2，就可以用y1进行分析。这就是两个变量的主成分分析！
那么，p个变量(x1,x2……xp)呢？
如前所述，我们希望找到x1,x2……xp的一些线性组合，它们互相独立，又能反映数据的大部分变异。这里称y1,y2……yp为主成分，事实上，有多少个变量就有多少个主成分。只不过为了研究问题的简便，我们会选择前几个主成分进行研究罢了。至于具体选几个，目前还没有明确的方法，要根据实际情况选取！
好了，有了主成分的概念之后，我们怎么求解得到这些主成分呢？是不是求得那些系数就好了呀。因为只是做应用，直接上结果了哈。对矩阵X计算协方差矩阵，求协方差矩阵特征值和特征向量。那么特征向量就是对应的系数。X如下：
是X的特征值。
如果系数是由特征向量得到的，那么特征值表示什么呢？特征值其实就是相应主成分的方差！如果有必要，可以对数据进行标准化，那么就是对相关矩阵进行谱分解啦~
我们求解出主成分之后，还有一项任务——解释主成分。一般而言，得到的主成分是原始变量的线性组合，于是常从权数较大的原始变量进行分析，看看主成分主要由哪些原始变量影响。
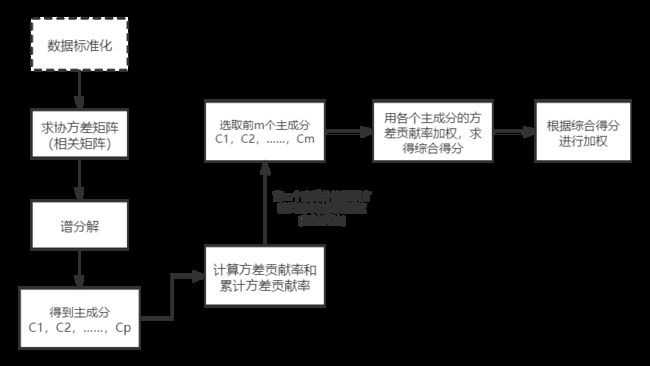
我们前面已经简要说明了主成分分析的求解过程，接下来说明主成分的分析过程，见图。
【提示】综合得分具体是这样的：
在R中，解决主成分分析会用到两个函数：princomp()和screeplot()。标准格式为：
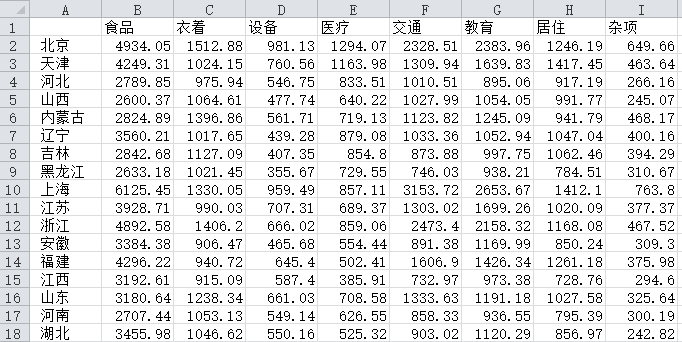
我们用主成分分析方法简单地对我国31个省、市、县、自治区的人均消费水平分析。
代码：
setwd('F:/R project/multi_analysis') data #数据处理 rowname data rownames(data) #主成分分析 pca #特征值(主成分方差) lamda lamda #载荷(系数) pca$loadings #方差贡献率和累积方差贡献率 var cumvar rbind(var,cumvar) #碎石图 screeplot(pca,type = 'lines') #得分 score score #计算综合得分(选取两个主成分) result result result$C result$rank #绘图 library(ggplot2) ggplot(result)+ geom_point(aes(Comp.1,Comp.2),shape = '*',size = 8,color = 'red')+ geom_hline(aes(yintercept = 0),linetype = 'dashed')+ geom_vline(aes(xintercept = 0),linetype = 'dashed')+ geom_text(aes(Comp.1,Comp.2,label = rownames(result)),size = 3,vjust = 'inward',hjust = 'inward')+ theme_classic()结果分析：
注：本次操作的数据在微信公众号后台回复data即可获取。
获得的数据(部分)如下：
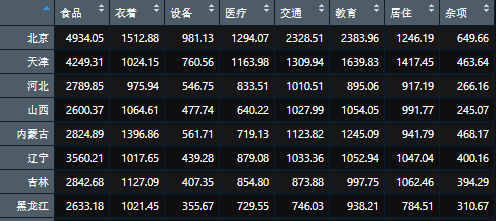
导入数据之后，应该做一下数据预处理。将第一列设置为数据框的行名，这个对于后面绘图很重要。处理完成之后的结果：
接着做主成分分析，你看，有了前人的包，一句命令就完事儿了！得到的pca对象包含了很多元素，主要有：
(1)sdev：每个主成分的标准误，将它平方就能得到主成分的方差，也即协方差矩阵或者相关矩阵的特征值。
(2)loadings：载荷。
(3)scores：主成分得分。
常用到的就是这些了。
因为得到的sdev并不是特征值，因此我这里进行了平方，得到方差。进一步计算得到方差贡献率var和累积方差贡献率cumvar(命名可能不是很规范，理解为主！)。按照主成分分析的流程，我们得到主成分之后要选择主成分的个数。常常用到的就是碎石图，将特征值从大到小排列，选取第一个拐弯点对应的序号即可。也可以按照之前计算的累积方差贡献率进行选择。碎石图如下：
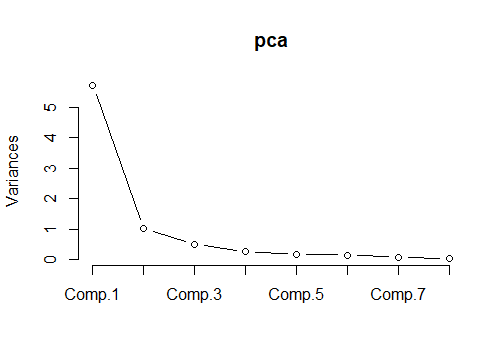
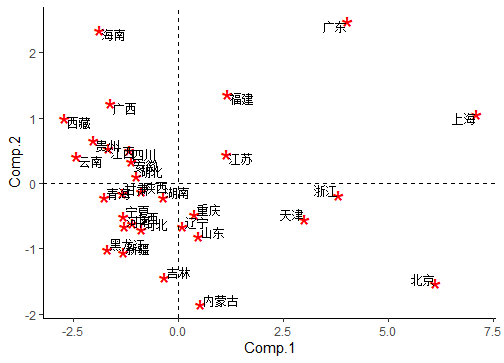
按照这个碎石图的结果，选取2个主成分比较好。事实上，我们会尽可能地选取2个主成分，因为这样方便进行可视化。选取了2个主成分之后，可以计算各个地区在这2个主成分下的得分，接着用方差贡献率加权求综合得分，计算排名。将本次主成分分析的结果可视化，得到的图形如下：
不过，这里还有一个遗留问题：两个主成分的含义怎么解释？
能得到载荷矩阵(前两个主成分)：
Comp.1 Comp.2 食品 0.3530160 0.42913372 衣着 0.2494594 -0.67707366 设备 0.3738401 0.08881424 医疗 0.3016294 -0.47157654 交通 0.3760539 0.32423582 教育 0.4040134 0.06946256 居住 0.3709635 0.05611496 杂项 0.3743738 -0.11849177第一个主成分好像在各个方面消费的载荷都较大，可以视为日常必需消费，第二个主成分在衣着消费上载荷较大，可以视为衣着消费。当然，这样的解释也是很含糊的，不像原始变量那样有确切含义。
主成分分析的介绍就到这里，接着再说因子分析。
因子分析——用少数不可观测的隐变量解释原始变量之间的关系因子分析是主成分分析的推广，其前提也是原始变量之间有较大的相关性。它的思路是将观测变量进行分类，把相关性较高的分在同一类，从每一类中提取出一个基本结构(即为公共因子，这些公共因子实际上是不可观测的)，并且用公共因子的线性组合和特殊因子来描述原始变量。到这里是不是对主成分分析和因子分析有点混淆？
主成分分析实际上就是一种线性组合，而因子分析却有一个模型——因子分析模型。
注意到：F1~Fm。也就是公共因子个数会比原始变量个数少！ε表示的是特殊因子，是公共因子解释不了的部分。
因子分析模型x=AF+ε有一些假定：
下面介绍常用的参数估计方法(用来估计A)。
主成分法
因子分析模型要求m
，所以：
这样，因子载荷矩阵A：
主因子法
这个方法是对主成分法的修正。如果随机向量x满足因子分析模型假定，则有：
我们引入约相关矩阵R*：
注意到：R与R*的区别在于主对角线不一样！
这里:
那主因子法就是先给
一个合适的估计值，这样就能得到约相关矩阵R*的初始估计值，然后对它进行谱分解，得到：
那么：
之后又进行谱分解……直到你满意为止。
是不是觉得这个方法更好一点？至少小白觉得还可以，可是这个方法运用到某些数据上可能不收敛！另外的初始估计值也很重要。
极大似然法
这里是假设公共因子
，特殊因子
，原始向量
由容量为n的一个样本得到似然函数
，找到满足下列条件的
：
判断这三种方法是否有效，可以通过样本的残差矩阵来判断。如果残差矩阵接近于0，说明方法是有效的。另外，通过理论推导，有以下结论：因子载荷aij是xi和Fj的协方差。
在R中实现因子分析用到的函数是factanal()。这个函数是基于极大似然方法来求解的，它的标准格式如下：
通过这些方法估计了公共因子之后，可以再继续旋转，使得更容易解释每个公共因子的含义。因子旋转主要是使因子载荷矩阵中的载荷绝对值向0和1两个方向分化。之前的主成分分析方法大多时候是不好解释的。因此，因子分析作为主成分分析的推广，通过旋转就能解决这个问题。具体怎么旋转就不说了~
前面在说主成分分析的时候说到了“主成分得分”，还记得吗？不记得就算了……言归正传，在因子分析中，也有一个得分——因子得分。实际上就是要求这些公共因子F1~Fm。小白前面也说过：F1~Fm是不可观测的，因此就只能估计啦。常用的估计方法有：加权最小二乘法和回归法。具体怎么估计的可以参见统计学相关教材。
下面通过具体的例子(水泥行业)演示。
代码：
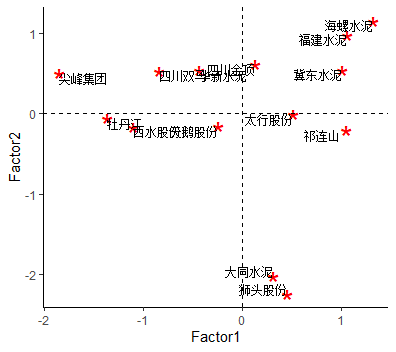
setwd('F:/R project/multi_analysis')data rownames(data) data #计算相关系数矩阵cor(data)#极大似然法fac #因子载荷fac$loadings#因子得分fac$scores#绘图library(ggplot2)result result ggplot(result)+ geom_point(aes(Factor1,Factor2),shape = '*',size = 8,color = 'red')+ geom_hline(aes(yintercept = 0),linetype = 'dashed')+ geom_vline(aes(xintercept = 0),linetype = 'dashed')+ geom_text(aes(Factor1,Factor2,label = rownames(result)),size = 3,vjust = 'inward',hjust = 'inward')+ theme_classic()结果分析：
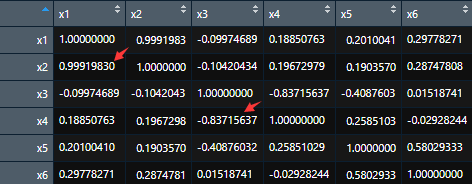
先计算相关矩阵，看看各个变量之间的相关性如何。如果不是很相关，就没必要进行下一步啦。得到的相关矩阵：
在这里，因子载荷如下：
Loadings: Factor1 Factor2x1 0.988 0.144 x2 0.987 0.148 x3 -0.997 x4 0.843 x5 0.137 0.415 x6 0.297旋转之后是不是拉得很开？这样就很方便解释了。这里x1~x6没有给出确切的含义，就不解释了。
因子得分如下：
Factor1 Factor2冀东水泥 1.0096908 0.54408248大同水泥 0.3062144 -2.01254136四川双马 -0.8417033 0.53208414牡丹江 -1.3645463 -0.06046795西水股份 -1.0956348 -0.16131972狮头股份 0.4561330 -2.23919392太行股份 0.5100995 -0.01095214海螺水泥 1.3134344 1.14981871尖峰集团 -1.8470313 0.50023508四川金顶 0.1312632 0.61251999祁连山 1.0424635 -0.20947603华新水泥 -0.4343916 0.53844498福建水泥 1.0600188 0.97776009天鹅股份 -0.2460105 -0.16099434通常得到这样的数据之后都要进行可视化：
到这里，小白基本上已经把主成分分析和因子分析的内容讲述完毕了，有什么问题请批评指正。今天就到这里啦~