NLP之Seq2Seq

参考文档：
①Seq2Seq简介1
②Seq2Seq简介2
③莫烦pythonB站视频
④莫烦python官网
⑤Luong论文

1 Seq2seq

Seq2Seq，又名编码器-解码器(Encoder-Decoder)，是一种输入为序列，输出也是序列的网络结构。

1.1 最简单的Seq2Seq结构

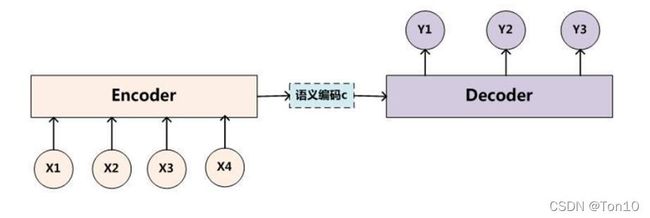
Encoder部分：输入的句向量在每一个时间步输入一个单词word或是一个标点。之后在最后一个时间步的隐藏状态表示这个句子的语义表征信息，即语义编码$c$向量。整个Encoder就是一个RNN(通常是LSTM或是GRU)。
Decoder部分：以语义编码c为输入，在每一个时间步输出单词word或是标点。整个Decoder就是个RNN(通常是LSTM或是GRU)。

1.2 具体例子

上图是Seq2Seq在翻译任务中的应用。输入是一个句子(“They are watching.”)，每一个时间步伐输入一个单词或标点，需要注意的是标点之后的末尾还有一个，表示句子的末尾符。Decoder的各个时间步的输出需要Encoder最后的语义信息、上一个时间步的输出以及上一个时间步的隐藏状态。

具体展开来说
Encoder编码：
Encoder的部分是由一个非定长序列转换成一个定长向量的过程。选用循环神经网络的一个重要原因是其包含序列次序信息。
设输入序列为$x_1,x_2,\cdots ,x_T$，则某事件步$t=a$时候RNN中隐藏层可表示为：
$$h_a=f_1(x_a,h_{a-1}).$$
而背景变量$c$的表示在Encoder的尾巴处，可表示为所有隐藏层输出的函数表示：
$$c=f_2(h_1,h_2,\cdots ,h_T).$$

Note：

1. 语义编码向量，即背景变量$c$，编码了整个输入序列$x_1,x_2,\cdots x_T$的信息。

Decoder解码
解码端也是一个RNN，其在时间步$t=b$时候隐藏层的输出取决于背景变量$c$、时间步$t=b$的输入以及前一个时间步的隐藏层输出$h_{b-1}$。
具体地，解码端隐藏层地表达式为：
$$h_b=f_3(y_{b-1},c,h_{b-1}).$$
而每个时间步，解码端输出地结果用概率表示为：
$$p(y_b|y_{b-1},y_{b-2},\cdots ,y_1,c).$$
Note:

1. 关于$y_{b-1}$：训练时候的Decoder和预测时候的Decoder是不同的：
   因为训练的时候Decoder是有标签来监督的，我们是基于正确的标签来输出预测的值：
   
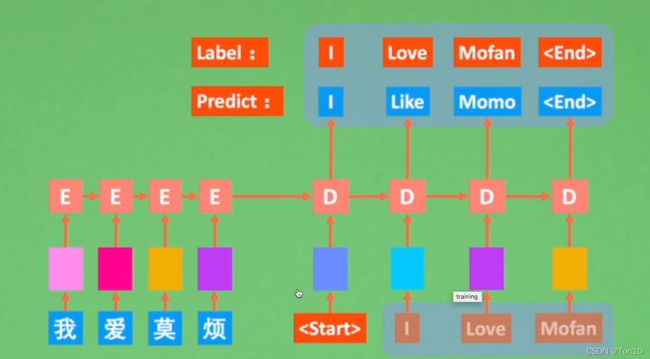
   而预测的时候基于测试集，所以没有标签，故每一个词的输出要取决于上一个词，按照一个接一个的顺序来解码：
   当然这两种方式并不是说第一种要在训练时候用，第二种要在inference时候用。第二种也可以在训练时候用，甚至混合起来也可以。

1.3 损失函数

Seq2Seq模型可以被建设成一个概率问题。即最大化似然估计：
$$\begin{gathered} P(y_1,\cdots ,y_{T^{\prime }}|x_1,\cdots ,x_T)=\prod _{t=1}^{T^{\prime }}p(y_t|y_{t-1},\cdots ,y_1,x_T,\cdots ,x_1) \\ =\prod _{t=1}^{T^{\prime }}p(y_t|y_{t-1},\cdots ,y_1,c)\text{\hspace{1em}(1)} \end{gathered}$$

1.4 优化(Beam Search)

接下去就是如何去优化式(1)，一般就有3种方式：贪婪搜索、穷举搜索、束搜索。

1.4.1 贪婪搜索

一个很自然的方式是使用贪婪搜索，贪婪的意思就是只关注于当下，只追求局部最优。
具体地，对于每一个时间步，我们会从$|\gamma |$个词中搜索出具有最大条件概率的词：
$$y_t=argma{x}_{y\in \gamma }P(y|y_{t-1},y_{t-2},\cdots ,y_1,c).$$一旦搜素出了或者达到了最大搜索长度$T^{\prime }$，就完成解码输出。

举个例子：

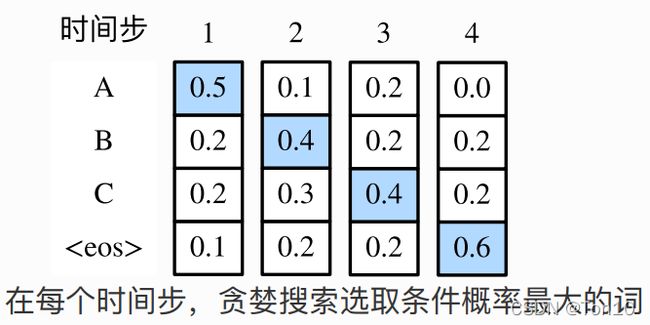
如上图所示，每一个时间步，都贪婪的选择最大概率对应的词，直到终止。目标函数的值为$0.5\ast 0.4\ast 0.4\ast 0.6=0.048$

上图在第二个时间步选择了第二概率大的词，也是正因为这一步的决策，使得第三步之后的概率分布发生变化。目标函数的值为$0.5\ast 0.3\ast 0.6\ast 0.6=0.054$。
从这里看出贪婪搜索已陷入局部最优，虽然简单但是无法找到最优的输出。

1.4.2 穷举搜索

穷举搜索也很简单，就是列举所有的情况，其复杂度为$O(|\gamma {|}^{T^{\prime }})$，显然这是不现实的，当字典大小$|\gamma |$很大的时候，会造成很大的计算开销与存储消耗。

1.4.3 束搜索

比如我们在预测到一半的时候，会发现之前预测的不太好，接下去要改善一下，就要用到束搜索。束搜索有个超参数：束宽$k$。每个事件步，都要从$k\cdot |\gamma |$个词中选取$k$个词。最后在所有的符合条件的序列中选取目标函数最大的序列即为输出序列。

举个例子，比如字典大小$|\gamma |=5$，最大输出长度$T^{\prime }=3$。

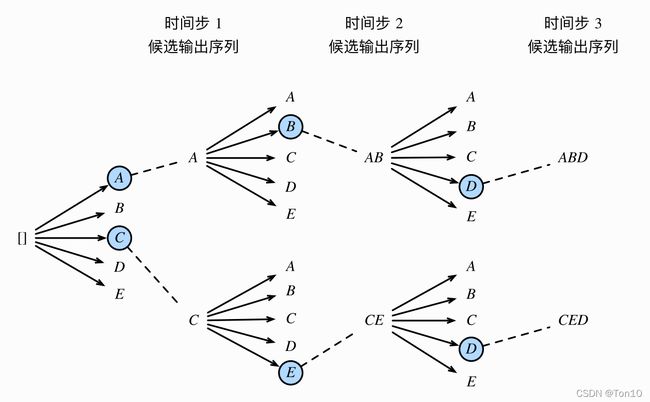
1. 首先选择前$k$个概率最大值，上图A和C。
2. 然后在10个词中选2个(每个字典选1个)，上图AB和CE。
3. 因为$T^{\prime }=3$，所以再从10个词($k\cdot |\gamma |$)选2个出来。
4. 最后在KaTeX parse error: Expected 'EOF', got '}' at position 20: …C、AB、CE、ABD、CED}̲中选出最合适的输出序列。

束搜索的复杂度为$O(k\cdot |\gamma |\cdot T^{\prime })$。他是介于贪婪搜索和穷举搜索之间的一种方法；当$k=1$时，束搜索就相当于是一种贪婪搜索。束搜索是计算资源和计算精确度之间的trade-off。

2 Attention(注意力机制)

注意力机制就如同他的名字一样，让模型训练更关注句子中的重点部分。
我们在第一节中提到Seq2Seq在解码端使用相同的背景变量$c$。

2.1 注意力机制的引入

举个例子：在翻译任务中，输入序列是英文"They are watching"，解码输出是法语"IIs regardent"。其中"They are"对应"IIs"，“IIs”在输出的时候其实只要背景变量能表征"They are"即可，而不需要整一段输入序列。换句话说解码端只需要把注意力集中在“They are”即可；同理"regardent"的翻译只需要背景变量$c$能表示"watching"就行了。
因此，我们希望在翻译不同的阶段可以针对输入的一部分，即对输入序列的某一部位集中注意力，让这一部分来决定我解码端的输出即可，这就是注意力机制的引入。

2.2 注意力机制

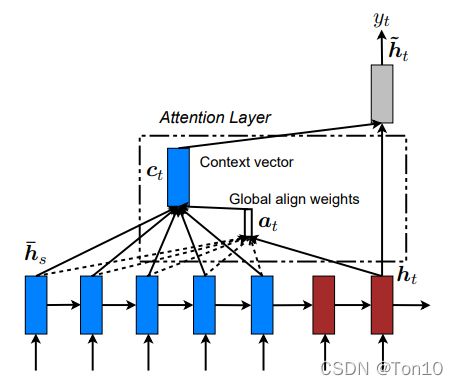
注意力机制通过对Encoder部分所有时间步的隐藏状态做加权平均来得到背景变量$c$，而不仅仅是第一节中一成不变的甚至只是Encoder最后一层隐藏层的输出来作为背景变量。特别的是，在解码端的每一个时间步，注意力机制会去调整这个权重，来对需要关注的Encoder部分给予较高的权重并编入更新背景变量$c$。
具体地，在解码端的时间步$t^{\prime }$，隐藏层的输出表示为：
$$h_{t^{\prime }}=f(y_{t^{\prime }-1},c_{t^{\prime }},h_{t^{\prime }-1}).$$其中$c_{t^{\prime }}$是更新的背景变量$c$。

2.3 背景变量的计算

上图展示了函数$a$如何在解码端时间步2计算背景变量。函数根据解码器在时间步1的隐藏状态和编码器在各个时间步的隐藏状态计算softmax运算的输⼊。Softmax运算输出概率分布并对编码器各个时间步的隐藏状态做加权平均，从⽽得到背景变量。
具体地：
解码端在时间步$t=x$处计算的背景变量为：
$$c_x=\sum _{t=1}^T{\alpha }_{x,t}{h}_t.$$其中$h_t$表示编码器所有时间步的隐藏层输出。
$\alpha$就是注意力权重，其获得依靠于softmax函数：
$${\alpha }_{x,t}=\frac{exp(e_{x,t})}{{\sum }_{k=1}^{T}exp(e_{x,k})},t=1,2,\cdots ,T.$$其中$e_{x,t}=a(h_{t^{\prime }-1},h_t)$，时间步带${}^{\prime }$表示是解码端的时间。
此外$a$的运算有多种方式：
①$a(h_1,h_2)=h_1^T{h}_2.$。
②$a(h_1,h_2)=v^{T}tanh(W_1{h}_1+W_2{h}_2)$，$v、W_1、W_2$都是可学习的模型参数。
③$h_1^{T}W{h}_2$，$W$是可学习的模型参数。
这里有一张关于注意力函数的表：

3 展望

1. 注意力机制启发了后续Transformer的发展，在当时这是一种全新的模型，其抛弃了CNN以及RNN的经典结构，在计算效率上大放异彩。
2. 除了NLP领域，注意力机制还被广泛用于图像分类、自动图像描述、唇语解读以及语⾳识别。
3. 束搜索部分是个寻优问题，其在一定程度上可以使用强化学习来做改善。