三点定圆推导公式
不共线的三个点可以确定一个圆。
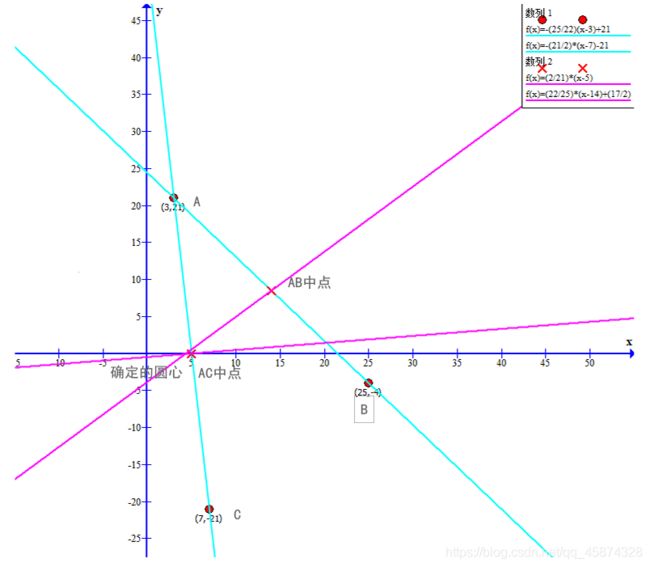
下图是用Graph画的一个很粗糙的图片用于方便理解。
紫色的线分别为AB的中垂线和AC的中垂线。
两个中垂线的交点就是圆心。
圆心到三个点的距离都相等。
推导公式
参考博客:三点确定一个圆的计算方法
设圆心坐标O为 ( x 0 , y 0 ) (x_0, y_0) (x0,y0),半径为r
三个点的坐标分别是,A ( x 1 , y 1 ) (x_1, y_1) (x1,y1),B ( x 2 , y 2 ) (x_2, y_2) (x2,y2),C ( x 3 , y 3 ) (x_3, y_3) (x3,y3)
三个点到圆心的距离相等
{ ( x 1 − x 0 ) 2 + ( y 1 − y 0 ) 2 = r 2 ( x 2 − x 0 ) 2 + ( y 2 − y 0 ) 2 = r 2 ( x 3 − x 0 ) 2 + ( y 3 − y 0 ) 2 = r 2 \left\{ \begin{array}{c} (x_1−x_0)^2+(y_1−y_0)^2=r^2 \\ \\ (x_2−x_0)^2+(y_2−y_0)^2=r^2 \\ \\ (x_3−x_0)^2+(y_3−y_0)^2=r^2 \end{array} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧(x1−x0)2+(y1−y0)2=r2(x2−x0)2+(y2−y0)2=r2(x3−x0)2+(y3−y0)2=r2
化简得到:
( x 1 − x 2 ) x 0 + ( y 1 − y 2 ) y 0 = ( x 1 2 − x 2 2 ) − ( y 2 2 − y 1 2 ) 2 (x_1-x_2)x_0 + (y_1-y_2)y_0 = \frac{(x_1^2-x_2^2)-(y_2^2-y_1^2)}{2} (x1−x2)x0+(y1−y2)y0=2(x12−x22)−(y22−y12)
( x 1 − x 3 ) x 0 + ( y 1 − y 3 ) y 0 = ( x 1 2 − x 3 2 ) − ( y 3 2 − y 1 2 ) 2 (x_1-x_3)x_0 + (y_1-y_3)y_0 = \frac{(x_1^2-x_3^2)-(y_3^2-y_1^2)}{2} (x1−x3)x0+(y1−y3)y0=2(x12−x32)−(y32−y12)
使用克拉默法则对行列式求解
∣ A ∣ = ∣ ( x 1 − x 2 ) ( y 1 − y 2 ) ( x 1 − x 3 ) ( y 1 − y 3 ) ∣ \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} (x_1-x_2) & (y_1-y_2) \\ \\ (x_1-x_3) & (y_1-y_3) \\ \end{vmatrix} ∣∣A∣∣=∣∣∣∣∣∣(x1−x2)(x1−x3)(y1−y2)(y1−y3)∣∣∣∣∣∣
∣ b ∣ = ∣ ( x 1 2 − x 2 2 ) − ( y 2 2 − y 1 2 ) 2 ( x 1 2 − x 3 2 ) − ( y 3 2 − y 1 2 ) 2 ∣ \begin{vmatrix} b \end{vmatrix} = \begin{vmatrix} \cfrac{(x_1^2-x_2^2)-(y_2^2-y_1^2)}{2} \\ \\ \cfrac{(x_1^2-x_3^2)-(y_3^2-y_1^2)}{2} \\ \end{vmatrix} ∣∣b∣∣=∣∣∣∣∣∣∣∣∣2(x12−x22)−(y22−y12)2(x12−x32)−(y32−y12)∣∣∣∣∣∣∣∣∣
∣ A 1 ∣ = ∣ ( x 1 2 − x 2 2 ) − ( y 2 2 − y 1 2 ) 2 ( y 1 − y 2 ) ( x 1 2 − x 3 2 ) − ( y 3 2 − y 1 2 ) 2 ( y 1 − y 3 ) ∣ \begin{vmatrix} A_1 \end{vmatrix} = \begin{vmatrix} \cfrac{(x_1^2-x_2^2)-(y_2^2-y_1^2)}{2} & (y_1-y_2) \\ \\ \cfrac{(x_1^2-x_3^2)-(y_3^2-y_1^2)}{2} & (y_1-y_3) \\ \end{vmatrix} ∣∣A1∣∣=∣∣∣∣∣∣∣∣∣2(x12−x22)−(y22−y12)2(x12−x32)−(y32−y12)(y1−y2)(y1−y3)∣∣∣∣∣∣∣∣∣
∣ A 2 ∣ = ∣ ( x 1 − x 2 ) ( x 1 2 − x 2 2 ) − ( y 2 2 − y 1 2 ) 2 ( x 1 − x 3 ) ( x 1 2 − x 3 2 ) − ( y 3 2 − y 1 2 ) 2 ∣ \begin{vmatrix} A_2 \end{vmatrix} = \begin{vmatrix} (x_1-x_2) & \cfrac{(x_1^2-x_2^2)-(y_2^2-y_1^2)}{2} \\ \\ (x_1-x_3) & \cfrac{(x_1^2-x_3^2)-(y_3^2-y_1^2)}{2} \\ \end{vmatrix} ∣∣A2∣∣=∣∣∣∣∣∣∣∣∣(x1−x2)(x1−x3)2(x12−x22)−(y22−y12)2(x12−x32)−(y32−y12)∣∣∣∣∣∣∣∣∣
x 1 = ∣ A 1 ∣ ∣ A ∣ x_1 = \cfrac{\begin{vmatrix}A_1\end{vmatrix}}{\begin{vmatrix}A\end{vmatrix}} x1=∣∣A∣∣∣∣A1∣∣ , x 2 = ∣ A 2 ∣ ∣ A ∣ x_2 = \cfrac{\begin{vmatrix}A_2\end{vmatrix}}{\begin{vmatrix}A\end{vmatrix}} x2=∣∣A∣∣∣∣A2∣∣
令
a = x 1 − x 2 b = y 1 − y 2 ; c = x 1 − x 3 ; d = y 1 − y 3 ; e = ( x 1 2 − x 2 2 ) − ( y 2 2 − y 1 2 ) 2 f = ( x 1 2 − x 3 2 ) − ( y 3 2 − y 1 2 ) 2 a = x_1 - x_2 \\ b = y_1 - y_2; \\ c = x_1 - x_3; \\ d = y_1 - y_3; \\ e = \cfrac{(x_1^2-x_2^2)-(y_2^2-y_1^2)}{2} \\ f = \cfrac{(x_1^2-x_3^2)-(y_3^2-y_1^2)}{2} a=x1−x2b=y1−y2;c=x1−x3;d=y1−y3;e=2(x12−x22)−(y22−y12)f=2(x12−x32)−(y32−y12)
则
x = e d − b f a d − b c x = \cfrac{ed-bf}{ad-bc} x=ad−bced−bf
y = a f − e c a d − b c y = \cfrac{af-ec}{ad-bc} y=ad−bcaf−ec
void function(double x1, double y1, double x2, double y2, double x3, double y3){
double a = x1 - x2;
double b = y1 - y2;
double c = x1 - x3;
double d = y1 - y3;
double e = ((x1*x1-x2*x2)-(y2*y2-y1*y1))/2;
double f = ((x1*x1-x3*x3)-(y3*y3-y1*y1))/2;
// 圆心位置
x = (e*d - b*f)/(a*d - b*c);
y = (a*f - e*c)/(a*d - b*c);
}