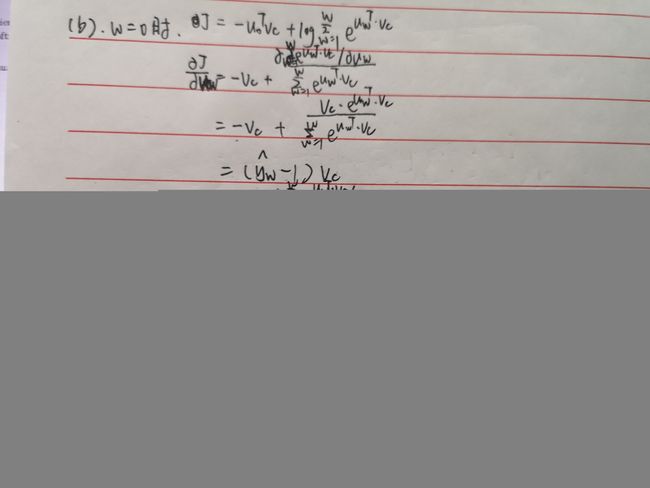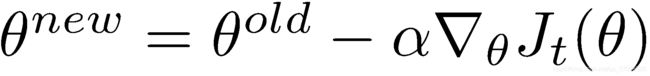CS224N刷题——Assignment1.3_word2vec
Assignment #1
3.word2vec
(a)假设已有一个与skip-gram模型的中心词c对应的预测词向量
，并使用word2vec模型中的softmax函数进行词预测：
其中w表示第w个词，
是词汇表中所有单词的“输出”词向量。假设在预测中使用交叉熵损失函数，单词o是预期单词（在one-hot标签向量中的第o个元素是1），推导关于的梯度。
提示：使用问题2中的符号会有帮助。例如，让
作为每个词的softmax预测的向量，
作为预期词的向量，损失函数为：
其中![U=[u_{1},u_{2},...,u_{W}]](http://img.e-com-net.com/image/info8/6bae247c9a8e44d78b4893f7d158ece6.gif){kind=small}
是所有输出向量组成的矩阵，确保声明了向量和矩阵的方向。
(b)推导上一题中“输出”词向量
的梯度（包括
）。
(c)使用负采样损失重新完成(a)和(b)，中心词向量为，期望的输出单词为o。假设采样了K个负采样单词，为了表示的简单性记为
（
），对于给定的单词o，记它的输出向量为。这种情况下的负采样的损失函数为：
其中
是sigmoid函数。
(d)给出前面的部分，并给出一组上下文词![[word_{c-m},...,word_{c-1},word_{c},word_{c+1},...,word_{c+m}]](http://img.e-com-net.com/image/info8/492dbac234564324bfb13009789d98d0.gif){kind=small}
，推导skip-gram和CBOW的所有词向量的梯度，其中m是上下文的大小。将单词
的“输入”词向量和“输出”词向量分别记作
和
。
提示：可以使用
（o是期望词）作为
或
损失函数中的占位符，这在程序部分是很有用的抽象化。则答案中可能会包含
。
对于skip-gram，中心词c的上下文的损失函数为：
其中
指的是距离中心词第j个索引的词。
CBOW略有不同，不使用作为预测向量，而是使用下面定义的
。对于CBOW，我们把上下文单词的输入词向量加起来：
则CBOW的损失函数为：
注：为了与的记号保持一致，例如代码部分，对于skip-gram
。
(e)实现word2vec模型并利用随机梯度下降法训练自己的词向量。
首先，写一个辅助函数用来归一化矩阵的行：
def normalizeRows(x):
""" Row normalization function
Implement a function that normalizes each row of a matrix to have
unit length.
"""
# YOUR CODE HERE
x = np.array([x_row / np.sqrt(np.sum(x_row**2)) for x_row in x])
# END YOUR CODE
return x然后，实现softmax和负采样损失函数和梯度：
def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
""" Softmax cost function for word2vec models
Implement the cost and gradients for one predicted word vector
and one target word vector as a building block for word2vec
models, assuming the softmax prediction function and cross
entropy loss.
Arguments:
predicted -- numpy ndarray, predicted word vector (\hat{v} in
the written component)
target -- integer, the index of the target word
outputVectors -- "output" vectors (as rows) for all tokens
dataset -- needed for negative sampling, unused here.
Return:
cost -- cross entropy cost for the softmax word prediction
gradPred -- the gradient with respect to the predicted word
vector
grad -- the gradient with respect to all the other word
vectors
We will not provide starter code for this function, but feel
free to reference the code you previously wrote for this
assignment!
"""
# predicted:(d,)
# outputVectors:(W, d)
# YOUR CODE HERE
W = len(outputVectors)
d = len(predicted)
y = np.zeros(shape=W)
y[target] = 1
y_hat_denominator = np.sum([np.exp(np.dot(u, predicted)) for u in outputVectors])
y_hat = np.array([np.exp(np.dot(outputVectors[i], predicted)) / y_hat_denominator for i in range(W)])
y_target_hat = y_hat[target]
cost = -np.log(y_target_hat)
gradPred = np.zeros(shape=d)
grad = np.zeros(shape=(W, d))
for w in range(W):
if w == target:
gradPred += (y_hat[w] - 1) * outputVectors[w]
grad[w] = (y_hat[w] - 1) * predicted
else:
gradPred += y_hat[w] * outputVectors[w]
grad[w] = y_hat[w] * predicted
# y_hat:(W,)
# y:(W,)
# gradPred:(d,)
# grad:(W,d)
# END YOUR CODE
return cost, gradPred, grad
def getNegativeSamples(target, dataset, K):
""" Samples K indexes which are not the target """
indices = [None] * K
for k in range(K):
newidx = dataset.sampleTokenIdx()
while newidx == target:
newidx = dataset.sampleTokenIdx()
indices[k] = newidx
return indices
def negSamplingCostAndGradient(predicted, target, outputVectors, dataset,
K=10):
""" Negative sampling cost function for word2vec models
Implement the cost and gradients for one predicted word vector
and one target word vector as a building block for word2vec
models, using the negative sampling technique. K is the sample
size.
Note: See test_word2vec below for dataset's initialization.
Arguments/Return Specifications: same as softmaxCostAndGradient
"""
# predicted:(d,)
# outputVectors:(W, d)
# Sampling of indices is done for you. Do not modify this if you
# wish to match the autograder and receive points!
indices = [target]
indices.extend(getNegativeSamples(target, dataset, K))
# YOUR CODE HERE
W = len(outputVectors)
d = len(predicted)
cost = -np.log(sigmoid(np.dot(outputVectors[target], predicted)))
gradPred = (sigmoid(np.dot(outputVectors[target], predicted)) - 1) * outputVectors[target]
grad = np.zeros(shape=(W, d))
for k in indices:
if k == target:
grad[k] = (sigmoid(np.dot(outputVectors[k], predicted)) - 1) * predicted
else:
cost -= np.log(sigmoid(-np.dot(outputVectors[k], predicted)))
gradPred -= (sigmoid(-np.dot(outputVectors[k], predicted)) - 1) * outputVectors[k]
grad[k] -= (sigmoid(-np.dot(outputVectors[k], predicted)) - 1) * predicted
# END YOUR CODE
return cost, gradPred, grad最后，实现skip-gram模型的损失函数和梯度：
def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors,
dataset, word2vecCostAndGradient=softmaxCostAndGradient):
""" Skip-gram model in word2vec
Implement the skip-gram model in this function.
Arguments:
currentWord -- a string of the current center word
C -- integer, context size
contextWords -- list of no more than 2*C strings, the context words
tokens -- a dictionary that maps words to their indices in
the word vector list
inputVectors -- "input" word vectors (as rows) for all tokens
outputVectors -- "output" word vectors (as rows) for all tokens
word2vecCostAndGradient -- the cost and gradient function for
a prediction vector given the target
word vectors, could be one of the two
cost functions you implemented above.
Return:
cost -- the cost function value for the skip-gram model
grad -- the gradient with respect to the word vectors
"""
# currentWord:一个单词
# C:上下文窗口大小
# contextsWords:上下文单词列表
# tokens:词对应索引的字典
# inputVectors:(5,3)
# outputVectors:(5,3)
cost = 0.0
gradIn = np.zeros(inputVectors.shape)
gradOut = np.zeros(outputVectors.shape)
# YOUR CODE HERE
predicted = inputVectors[tokens[currentWord]]
for target in contextWords:
dcost, dgradPred, dgrad = word2vecCostAndGradient(predicted, tokens[target], outputVectors, dataset)
# dgradPred:(3,)
# dgrad:(5,3)
cost += dcost
gradIn[tokens[currentWord]] += dgradPred
gradOut += dgrad
# END YOUR CODE
return cost, gradIn, gradOut结果如下：
Testing normalizeRows...
[[0.6 0.8 ]
[0.4472136 0.89442719]]
==== Gradient check for skip-gram ====
Gradient check passed!
Gradient check passed!
=== Results ===
(11.16610900153398, array([[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ],
[-1.26947339, -1.36873189, 2.45158957],
[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ]]), array([[-0.41045956, 0.18834851, 1.43272264],
[ 0.38202831, -0.17530219, -1.33348241],
[ 0.07009355, -0.03216399, -0.24466386],
[ 0.09472154, -0.04346509, -0.33062865],
[-0.13638384, 0.06258276, 0.47605228]]))
(16.15119285363322, array([[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ],
[-4.54650789, -1.85942252, 0.76397441],
[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ]]), array([[-0.69148188, 0.31730185, 2.41364029],
[-0.22716495, 0.10423969, 0.79292674],
[-0.45528438, 0.20891737, 1.58918512],
[-0.31602611, 0.14501561, 1.10309954],
[-0.80620296, 0.36994417, 2.81407799]]))
(f)实现SGD优化器。
def sgd(f, x0, step, iterations, postprocessing=None, useSaved=False,
PRINT_EVERY=10):
""" Stochastic Gradient Descent
Implement the stochastic gradient descent method in this function.
Arguments:
f -- the function to optimize, it should take a single
argument and yield two outputs, a cost and the gradient
with respect to the arguments
x0 -- the initial point to start SGD from
step -- the step size for SGD
iterations -- total iterations to run SGD for
postprocessing -- postprocessing function for the parameters
if necessary. In the case of word2vec we will need to
normalize the word vectors to have unit length.
PRINT_EVERY -- specifies how many iterations to output loss
Return:
x -- the parameter value after SGD finishes
"""
# Anneal learning rate every several iterations
ANNEAL_EVERY = 20000
if useSaved:
start_iter, oldx, state = load_saved_params()
if start_iter > 0:
x0 = oldx
step *= 0.5 ** (start_iter / ANNEAL_EVERY)
if state:
random.setstate(state)
else:
start_iter = 0
x = x0
if not postprocessing:
postprocessing = lambda x: x
expcost = None
for iter in range(start_iter + 1, iterations + 1):
# Don't forget to apply the postprocessing after every iteration!
# You might want to print the progress every few iterations.
cost = None
# YOUR CODE HERE
cost, grad = f(x)
x -= step * grad
postprocessing(x)
# END YOUR CODE
if iter % PRINT_EVERY == 0:
if not expcost:
expcost = cost
else:
expcost = .95 * expcost + .05 * cost
print("iter %d: %f" % (iter, expcost))
if iter % SAVE_PARAMS_EVERY == 0 and useSaved:
save_params(iter, x)
if iter % ANNEAL_EVERY == 0:
step *= 0.5
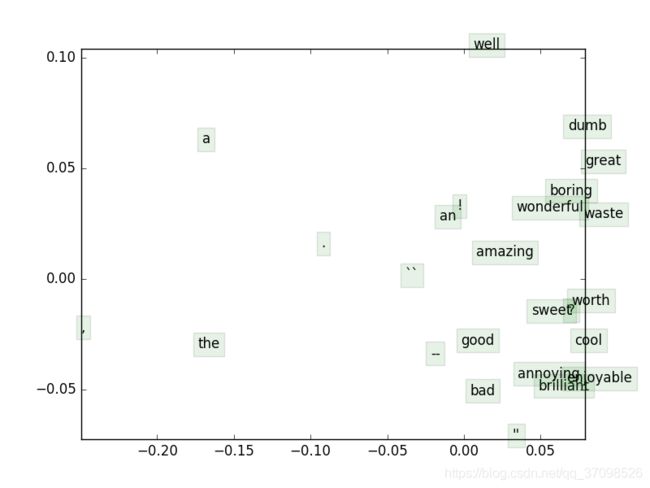
return x(g)现在开始加载真实数据并训练上述实现的词向量，训练词向量使用的是Stanford Sentiment Treebank(SST)数据集，之后使用它们完成一个简单的情感分类任务。首先运行sh get_datasets.sh获取数据集，然后运行q3_run.py，得到可视化的词向量：
