DeepLearning:训练神经网络—梯度下降优化器(optimizer)
训练神经网络—梯度下降优化器(optimizer)
文章目录
- 训练神经网络—梯度下降优化器(optimizer)
-
- 1、optimizer简介
-
- 定义
- 分类
-
- 一阶优化算法
- 二阶优化算法
- 优化器伪代码
- 2、SGD(随机梯度下降)
-
- 背景
-
- Q&A
- 定义
- 伪代码
- 3、SGD+Momentum(SGD结合动量)
-
- 定义
- 公式
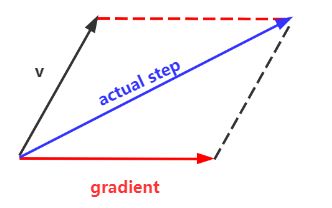
- 示意图
- 伪代码
- 4、Nesterov Momentum(梯度加速法)
-
- 背景
- 定义
- 公式
- 示意图
- 伪代码
- 5、AdaGrad
-
- 背景
- 伪代码
- 6、RMSProp(Leaky AdaGrad)
-
- 背景
- 伪代码
- 7、Adam
-
- 背景
- Adam(almost)
- Adam(full form)
- 8、小结
1、optimizer简介
定义
优化器其实可以看做我们的下山策略,其作用是通过改善训练方式来最小化(或最大化)损失函数E(x)。
分类
优化算法分为两大类:一阶优化算法和二阶优化算法,我主要介绍的是一阶优化算法。
一阶优化算法
一阶优化算法用时使用各参数的梯度值来最大或最小化损失函数f(x),常用的一阶优化算法是梯度下降。
二阶优化算法
使用了二阶导数(海森矩阵)来最小化或最大化损失函数,由于维数过高导致二阶导数计算成本很高,这种方法并不常用。
优化器伪代码
while True:
#其中evaluate_gradient是反向传播求得的梯度,loss_fun是前向传播的损失函数
#step_size是学习率
#the evaluate_gradient is the gradient which produced in backward prop
#the loss_fun means the loss function
#step_size is the learning rate
weights_grad = evaluate_gradient(loss_fun,data_weights)
weights += - step_size * weights_grad
2、SGD(随机梯度下降)
背景
原来,我们使用传统梯度下降的方式来进行参数优化,但是传统梯度下降具有自己的缺点:
①计算整个数据集梯度,但只会进行一次更新,因此在处理大型数据集时速度很慢且难以控制,甚至导致内存溢出。
②当我们希望在某一个方向优化的多一些时,很难做到,损失函数值会在梯度较大的方向上发生振荡,不能通过单纯减小学习率来解决,因为如果单纯减小学习率,则会让优化方向改变的更少。
③陷入局部最优点,鞍点(在高维空间中更普遍)。
Q&A
鞍点与局部最优点区别?
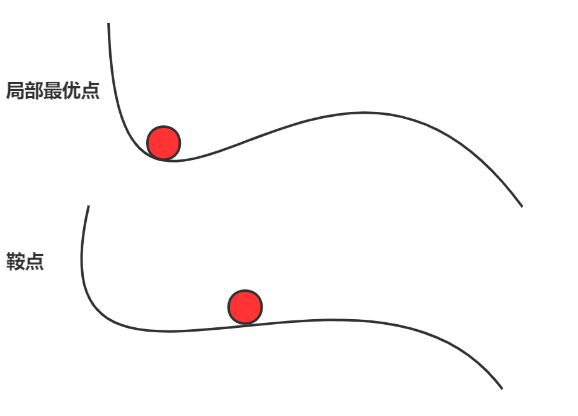
从上图可以看出局部最优点陷入“盆地”,而鞍点梯度为0。
损失函数:
L ( w ) = 1 N ∑ i = 1 N L i ( x i , y i , w ) L\left( w \right) =\frac{1}{N}\sum_{i=1}^N{\begin{array}{c} L_i\left( x_i,y_i,w \right)\\ \end{array}} \\ L(w)=N1i=1∑NLi(xi,yi,w)
梯度:
∇ w L ( w ) = 1 N ∑ i = 1 N ∇ w L i ( x i , y i , w ) \nabla wL\left( w \right) =\frac{1}{N}\sum_{i=1}^N{\nabla wL_i\left( x_i,y_i,w \right)} ∇wL(w)=N1i=1∑N∇wLi(xi,yi,w)
定义
随机梯度下降(SGD)对每个训练样本进行参数更新,每次执行都进行一次更新,且执行速度更快。
在SGD中,如何更快更好地下山?
x t + 1 = x t − α ∇ f ( x t ) x_{t+1}=x_t-\alpha \nabla f\left( x_t \right) xt+1=xt−α∇f(xt)
伪代码
while True:
dx = compute_gradient(x)
x -= learning_rate * dx
3、SGD+Momentum(SGD结合动量)
定义
SGD具有高方差震荡的缺点,这会使网络很难稳定收敛,所以有的学者提出了结合**动量(Momentum)**的技术,通过优化相关方向的训练和弱化无关方向的震荡来加速SGD训练,也就是使用动量。
这是一种结合到我们高中所学加速度的思想。
公式
v t + 1 = ρ v t + ∇ f ( x t ) x t + 1 = x t − α v t + 1 v_{t+1}=\rho v_t+\nabla f\left( x_t \right) \\ x_{t+1}=x_t-\alpha v_{t+1} vt+1=ρvt+∇f(xt)xt+1=xt−αvt+1
示意图
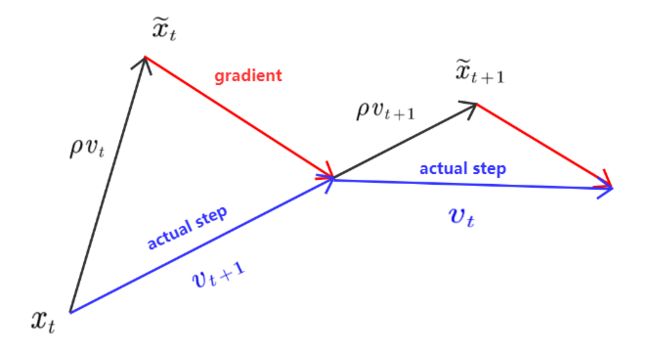
伪代码
while True:
dx = compute_gradient(x)
vx = rho * vx +dx
x -= learning_rate * vx
4、Nesterov Momentum(梯度加速法)
背景
利用动量存在一些问题,如果一个滚下山坡的小球盲目沿着斜坡下滑这是不“聪明”的,一个“聪明”的球应该注意到它要去哪,比如当山坡向上倾斜时,小球应当减速。实际中,当小球达到曲线上的最低点时,动量相当高,由于高动量可能会导致其完全错过最小值。因此,我们可以利用Nestrov梯度加速法解决栋梁问题。
定义
在Nestrov方法中,应根据之前动量进行大幅度跳跃,然后计算梯度进行矫正,从而实现参数更新。通过这种预更新的方法,能够防止大幅震荡,不会错过最小值,并对参数更新更加敏感。
公式
v t + 1 = ρ v t − α ∇ f ( x t + ρ v t ) x t + 1 = x t + v t + 1 x ~ t = x t + ρ v t v t + 1 = ρ v t − α ∇ f ( x ~ t ) x ~ t + 1 = x ~ t − ρ v t + ( 1 + ρ ) v t + 1 = x ~ t + v t + 1 + ρ ( v t + 1 − v t ) v_{t+1}=\rho v_t-\alpha \nabla f\left( x_t+\rho v_t \right) \\ x_{t+1}=x_t+v_{\begin{array}{c} t+1\\ \end{array}} \\ \tilde{x}_t=x_t+\rho v_t \\ v_{t+1}=\rho v_t-\alpha \nabla f\left( \tilde{x}_t \right) \\ \tilde{x}_{t+1}=\tilde{x}_t-\rho v_t+\left( 1+\rho \right) v_{t+1} \\ \,\, =\tilde{x}_t+v_{t+1}+\rho \left( v_{t+1}-v_t \right) vt+1=ρvt−α∇f(xt+ρvt)xt+1=xt+vt+1x~t=xt+ρvtvt+1=ρvt−α∇f(x~t)x~t+1=x~t−ρvt+(1+ρ)vt+1=x~t+vt+1+ρ(vt+1−vt)
示意图
伪代码
while True:
dx = compute_gradient(x)
old_v = v
v = roh*v -learning_rate * dx
x += -rho * old_v + (1+rho) * v
5、AdaGrad
背景
我们知道SGD的弊端是在梯度较大的方向上会发生振荡,那么AdaGrad就是通过在梯度较大的方向上增加一个惩罚项的优化方法。在AdaGrad中梯度陡的方向会被惩罚,梯度缓的方向会被加速优化,随着训练时间的增加,x的更新量会因为grad_squared的不断增大而减小,最后会衰减到0,导致学习速度越来越小,模型的学习能力迅速降低,而且收敛速度非常缓慢,需要很长的训练和学习时间,这也是AdaGrad的主要缺点。
伪代码
grad_squard = 0
while True:
dx = compute_gradient(x)
grad_squared += dx * dx
# 惩罚项是越来越大的,则分母越来越大,更新的就会越来越少
x -= learning_rate * dx /(np.sqrt(grad_squared+1e-7))
# 1e-7是为了防止分母为0
从上述代码可以看出AdaGrad更新的量在后期会越来越小,即使滚到了梯度很大的方向上也不会像其他优化器一样飞快滚下山。
6、RMSProp(Leaky AdaGrad)
背景
引入衰减因子以改善AdaGrad不能快速收敛的缺点。
伪代码
grad_squared = 0
while True:
dx = compute_gradient(x)
grad_squared = decay_rate*grad_squared+(1-decay_rate)*dx*dx
#decay_rate就是引入的衰减因子,反映保留多少我们之前的惩罚项
#若decay_rate变为1,则更新项变成0
#若decat_rate变为0,则不考虑之前的惩罚项
x -= learning_rate * dx /(np.sqrt(grad_squared)+1e-7)
7、Adam
背景
结合AdaGrad和RMSProp利用了第一动量和第二动量,其中第一动量参数值我们常设为0.9,第二动量参数值我们常设为0.999,学习率为0.001或0.0005。
Adam(almost)
first_moment = 0
second_moment = 0
#上面的两个参数只有长时间训练才会真正发挥作用
while True:
dx = compute_grandient(x)
#第一动量
first_moment = beta1*first_moment+(1-beta1)*dx
#第二动量
second_moment = beta2*second_moment+(1-beta2)*dx*dx
x -= learning_rate * first_moment/(np.sqrt(second_moment)+1e-7)
Adam(full form)
first_moment = 0
second_moment = 0
for i in range(1,num_iterations):
dx = compute_graient(x)
first_moment = beta1 * first_moment + (1 - beta1) * dx
second_moment = beta2 * second_moment + (1 - beta2) * dx * dx
first_unbias = first_moment/(1-beta1**t)
second_unbias = second_moment/(1-beta2**t)
x -= learning_rate * first_unbias / (np.sqrt(second_unbias)+1e-7)
8、小结
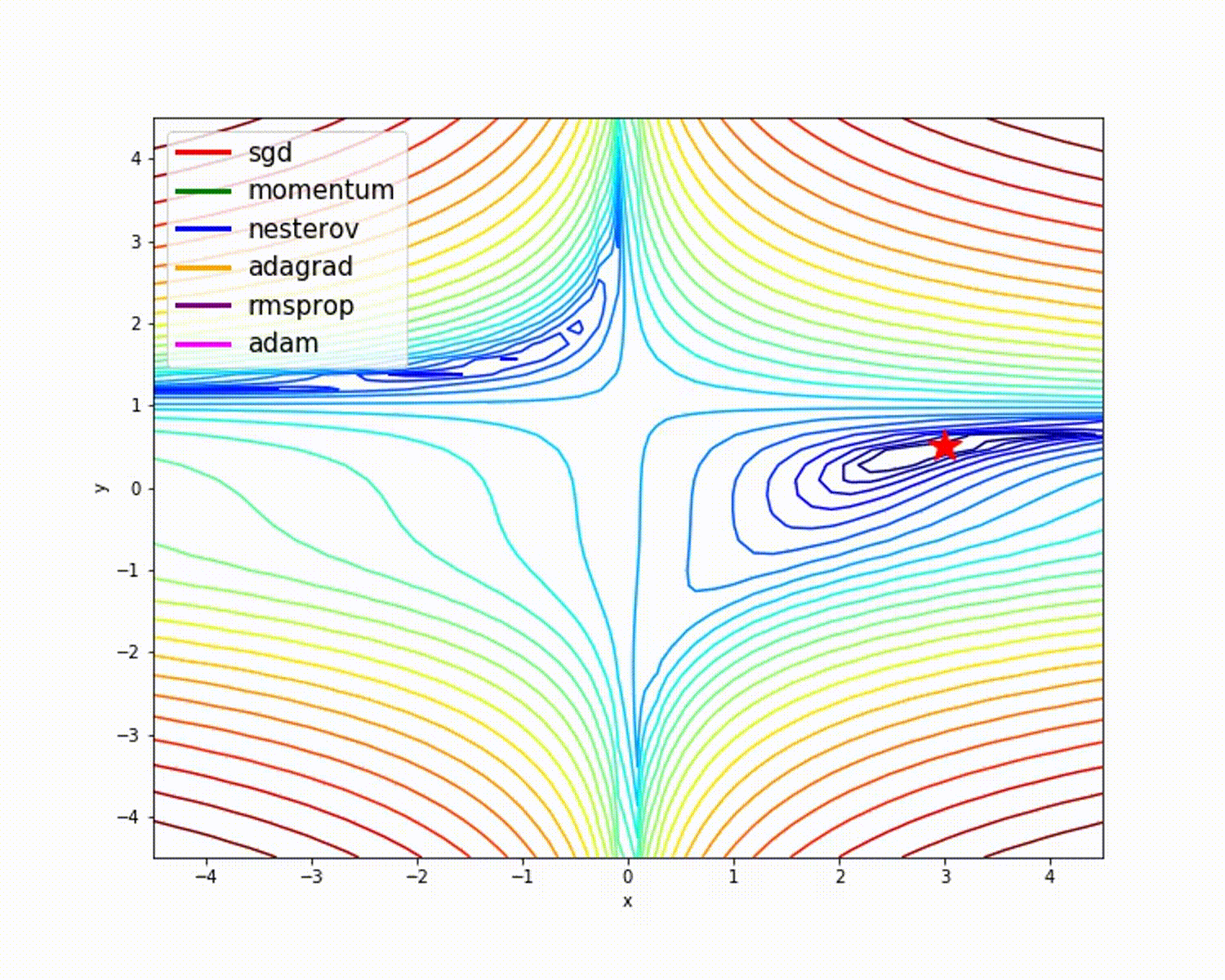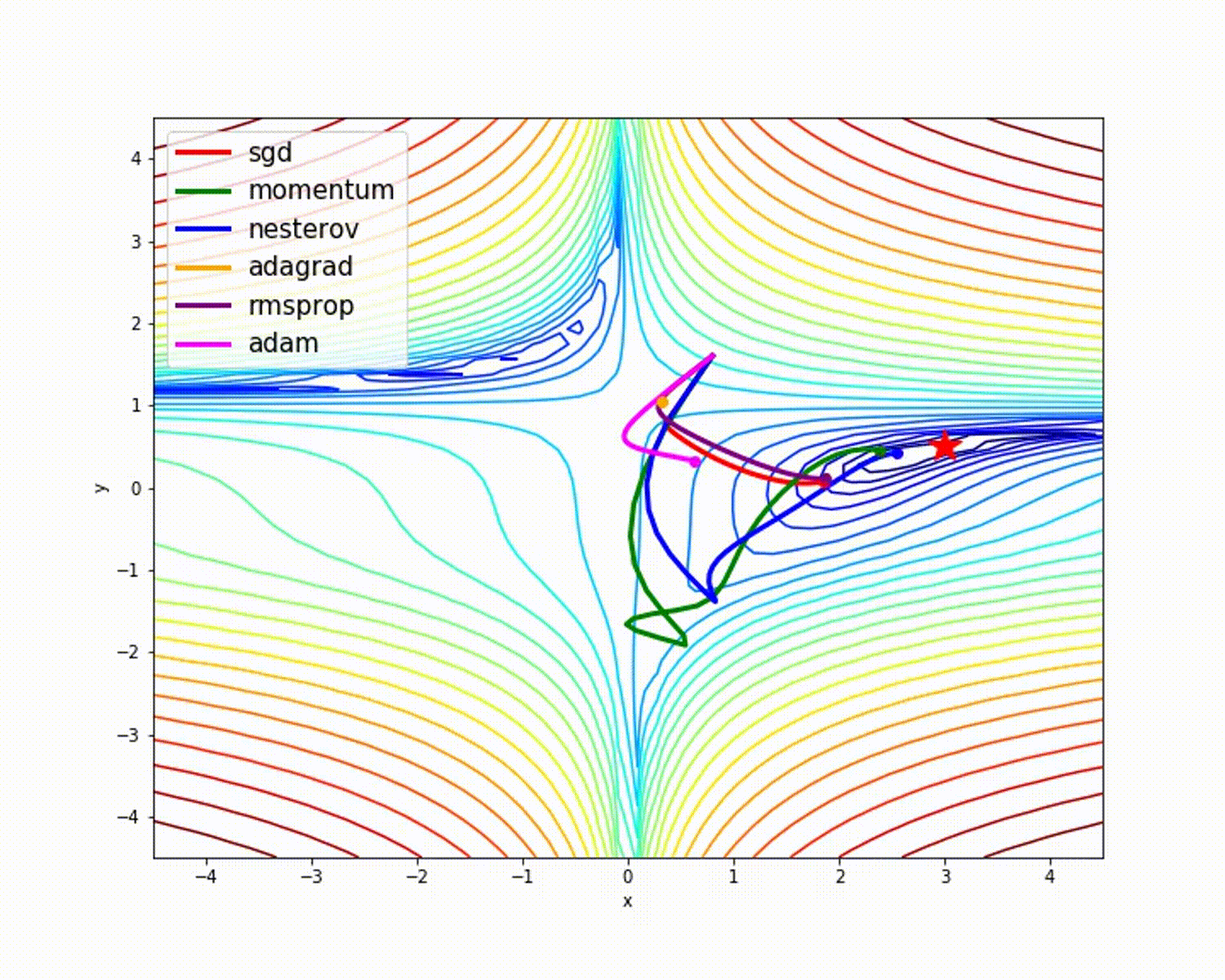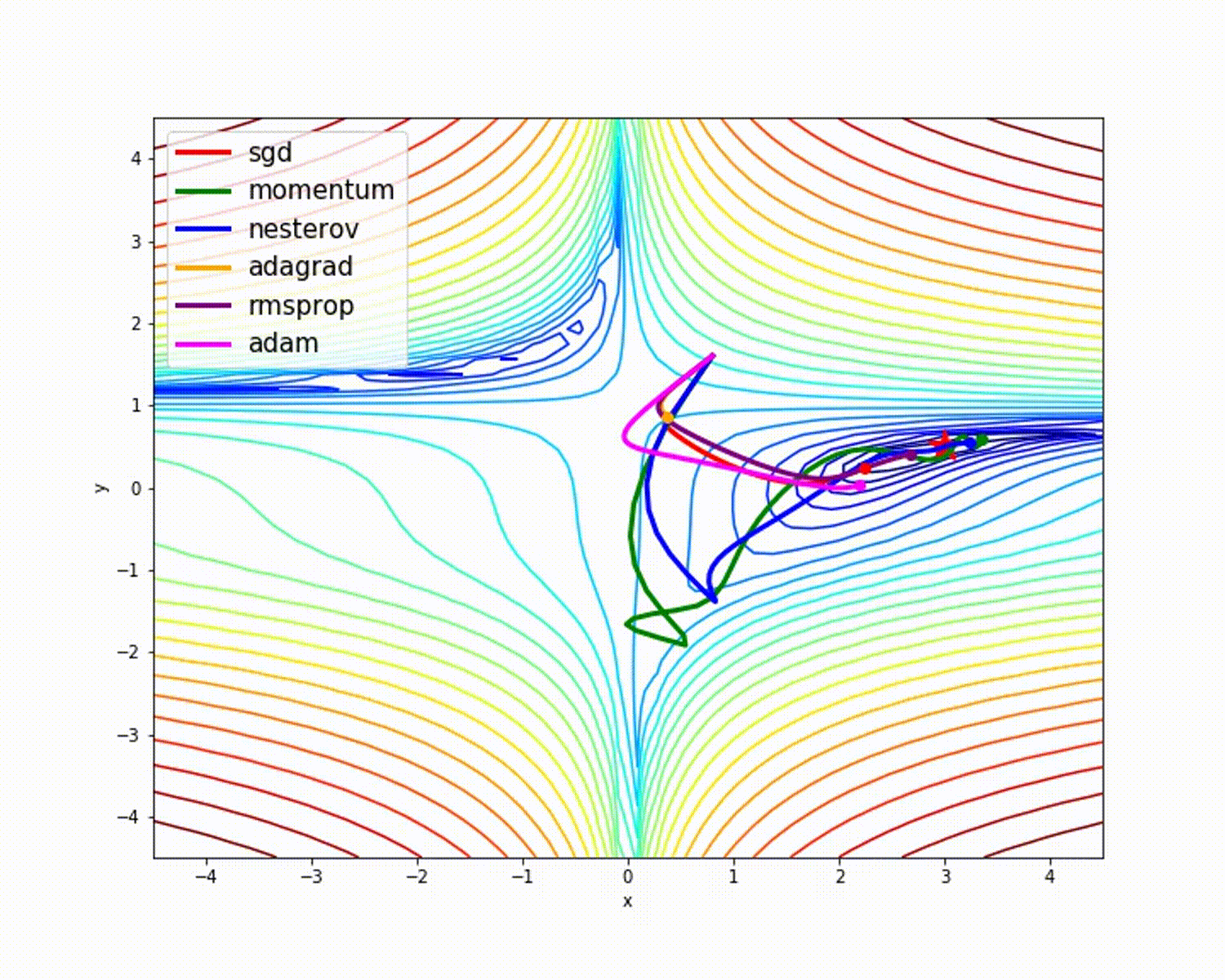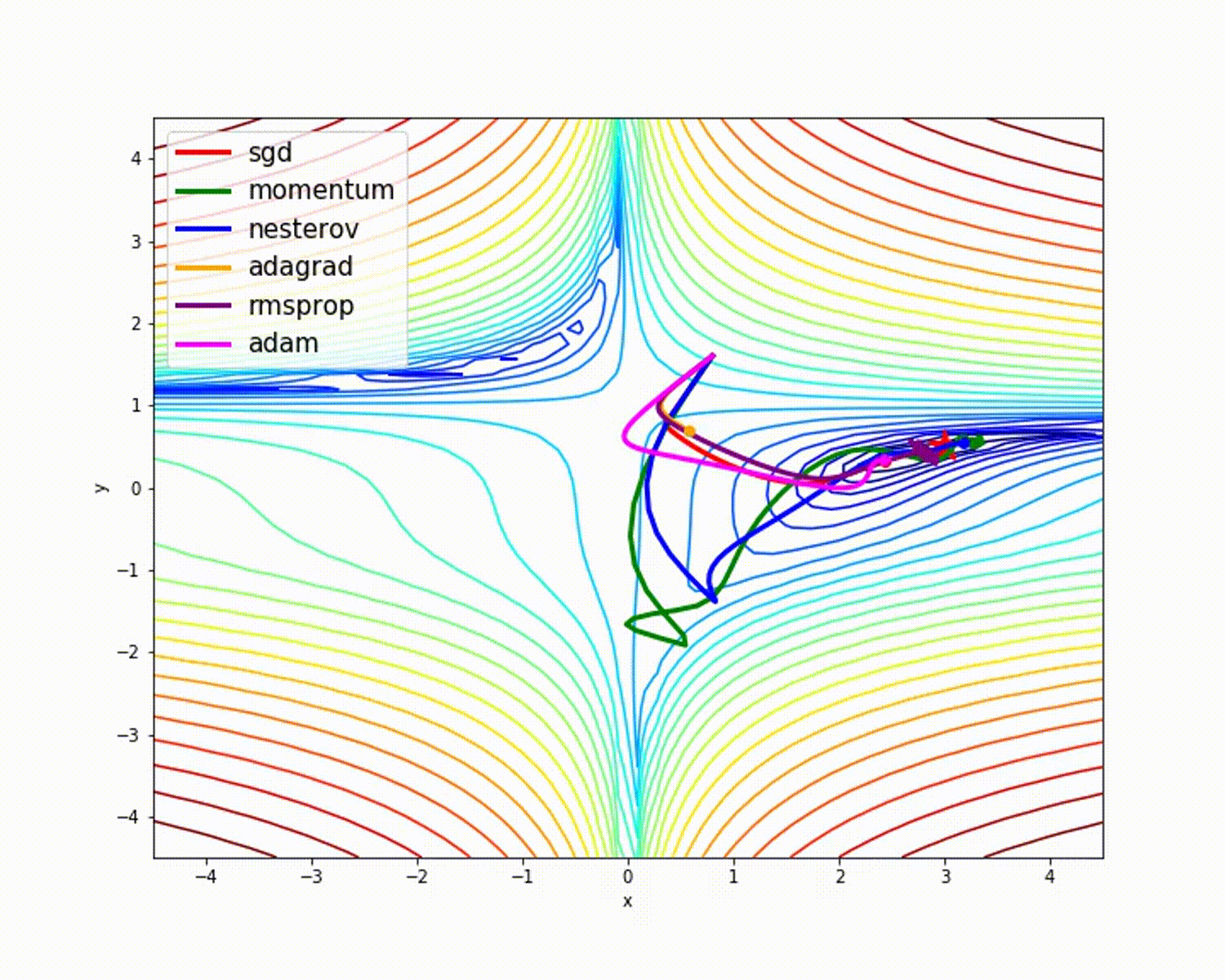
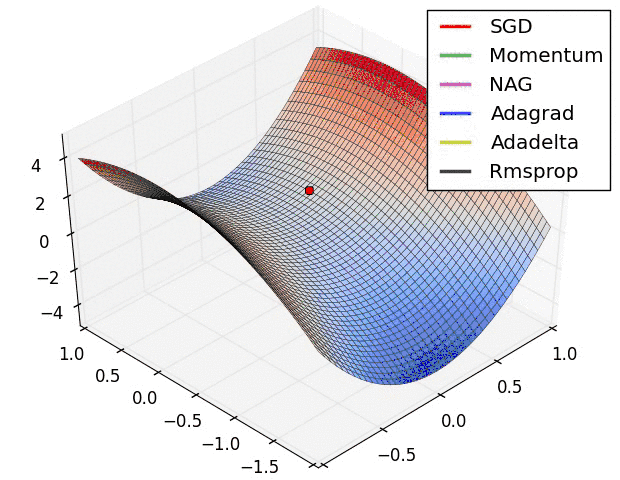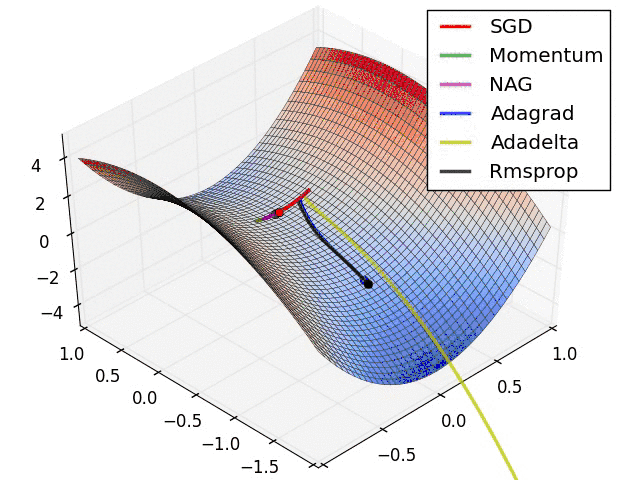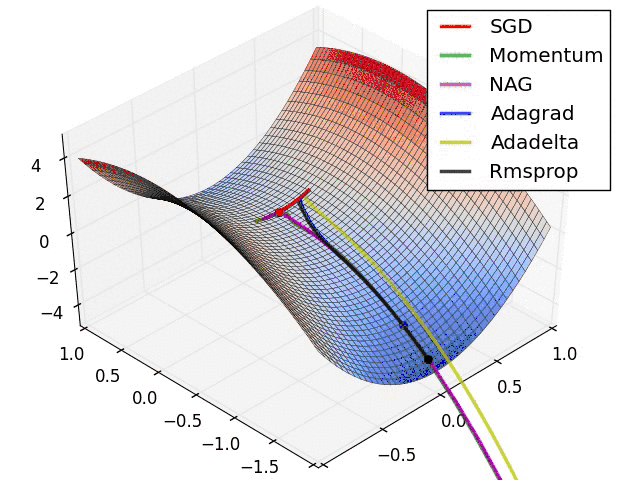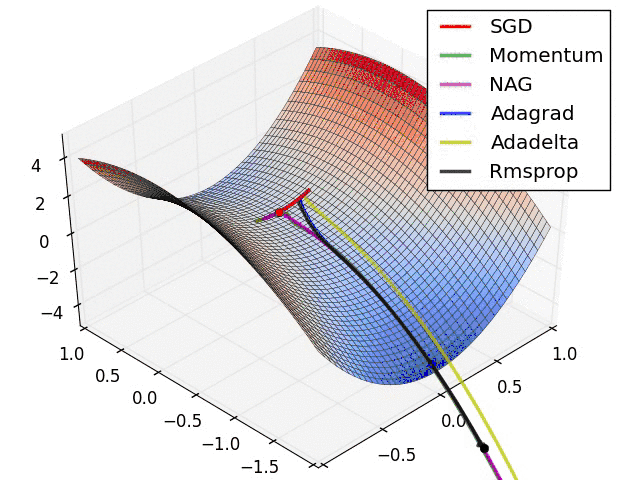
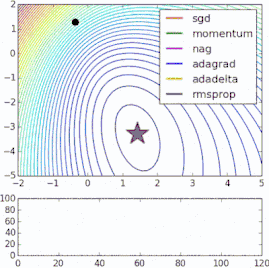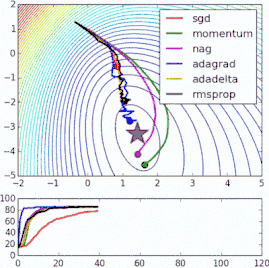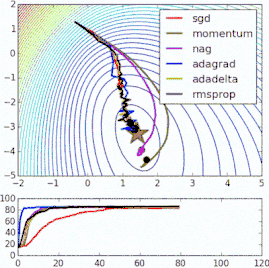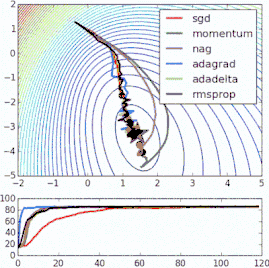
我们放一些动态图,直观的观察这些优化器的区别:
`