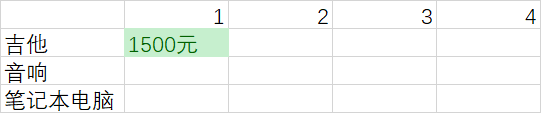写在前面
动态规划是算法里非常重要的一个分支,如果学不会动态规划,那想在算法竞赛和面试里占据一席之地几乎是不可能的事情
可是动归和搜索不同,深搜和宽搜都有一定的模板,所以一旦学会了,基本上可以解开绝大多数的题目
打算动归没有模板,更多的是一种思维,所以学起来会比较吃力
情景设计
假设我们是职业小偷,背包出门偷东西
我们假设背包的承受重量是4kg
摆在我们面前的有三种商品
A.音响【3000元,4kg】
B.笔记本电脑【2000元,3kg】
C.吉他【1500元,1kg】
当然小孩子才做选择,成年人选择全都要【开个玩笑】
由于我们的背包空间是有限的,所以只能选择偷最高价值的商品
简单算法
最简单的都是把所有的可能性都列出来
【1】放弃偷窃【0元,0kg】
【2】偷吉他【C】【1500元,1kg】
【3】偷音响【A】【3000元,4kg】
【4】笔记本电脑【B】【2000元,3kg】
【5】偷吉他和音响【CA】【装不下】
【6】偷吉他和笔记本电脑【CB】【3500元,4kg】
【7】偷音响和笔记本电脑【AB】【装不下】
【8】全部偷走【ABC】【装不下】
这样虽然可行,但是速度太慢了,等我们考虑完,估计警察已经在背后站半天了
动态规划
这个是就要引出动态规划
我们先来看看动态规划算法的工作原理
动态规划简单地说就是先解决子问题,再解决母问题
当然这个概念比较难理解,请同学们慢慢看
我们回到刚才的问题
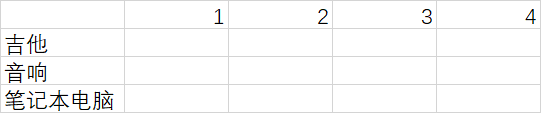
网格的各行为商品,各列为不同容量( 1~4kg)的背包。所有这些列你都需要,因为它们将帮助你计算子背包的价值。
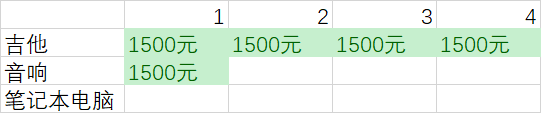
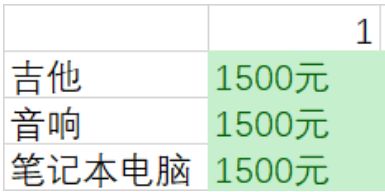
首先来看第一行,意味着我们要尝试偷吉他【但是到底偷不偷不一定,别忘了初心,我们是为了偷走最高价值的商品】
第一个单元格表示背包的容量为一kg。
吉他的重量也是一kg,这意味着可以装入背包
这个单元格包含吉他,价值为1500美元
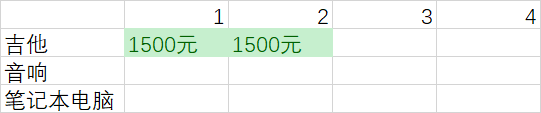
与这个单元格一样,每个单元格表示背包的容量为2kg,可以装下吉他
同学们可能对这个表格云里雾里,但是这里是假设只有吉他可以偷
这里同学们肯定会认为我在搞什么无聊的事情
但别忘了,我们之前说过
动态规划简单地说就是先解决子问题,再解决母问题
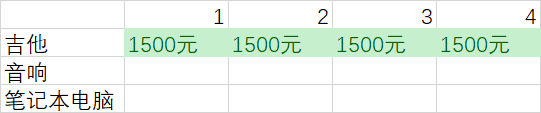
当前这张图是表示,如果有一个容量4kg的背包,可在其中装入的商品的最大价值为1500美元
当然肯定这不是最终的答案
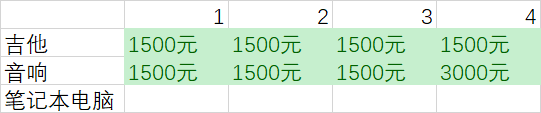
接下来我们放入音响
在每一行可偷得商品都为当前行的商品以及之前各行的商品
这表示我们现在只能偷影响和吉他
第一行第一列表示
背包容量为1kg时,之前可装入商品的最大价值
第二行第一列表示
我们要用1kg的背包,在同时能偷吉他和音响的情况下,现在可装入的商品的最大价值
我们得出的结论是背包的容量只有1kg的时候,我们偷不了音响
所以这时候我们能偷的最贵东西仍然是1500元
后面的结论是一样的
到第二行第四列的时候,我们发现背包容量为4kg的时候
最大的价值更新为3000元
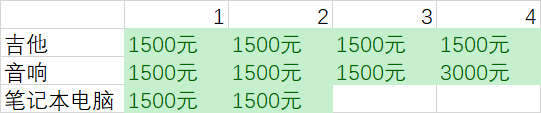
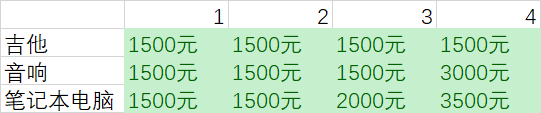
最后我们加入笔记本电脑
但是这时候问题来了
背包容量为3kg的时候,我们可以偷的东西选择性变大了,我们可以放弃吉他而去偷笔记本电脑,所以最大的价值更新为2000元
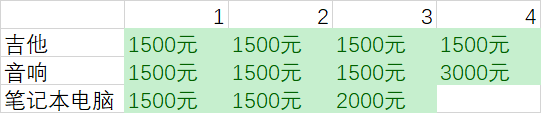
总算来到了最后的问题
对于容量为4kg的背包,情况很有趣
这是非常重要的部分
当前最大价值为3000元,你可以不偷音响,而偷笔记本电脑,但只价值2000元
那我们势必面临一个问题
3000元的音响 VS 2000元的笔记本电脑+1kg的空余容量
同学们发现没有,之前在1kg的容量中我们可加入的最大价值是多少?
答案是1500元
这个时候就可以作比较了
3000元【音响】 VS 2000元【笔记本电脑】+1500元【吉他】
同学们现在是否明白了为什么要计算小背包可装入了商品的最大价值
这样余下的空间我们不必再花大量的时间去做计算
答案如下,将吉他和笔记本电脑装入背包时价值最高,为3500美元
同学们听到这里可能还是有点疑惑,其实每个单元格的价值,使用的公示都相同
cell[i][j]=上一个单元的价值cell[i-1][j]VS当前商品的价值+剩余空间的价值
你可以使用这个公式来计算每个单元格的价值,最终的网格将与前一个网格相同。
现在你明白了为何要求解子问题吧?你可以合并两个子问题的解来得到更大问题的解。
拓展内容
增加一件商品
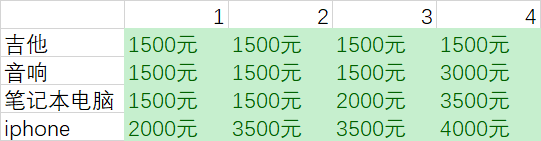
我们再玩点刺激的,加入第四件商品,一个iphone【2000元,1kg】
此时我们要不要推到重来?
根本不需要,动态规划主笔计算最大的值,我们之前做的事情,完全可以继续做
在第四行,加入iphone
当然为了方便同学们看清楚
我再重新列一下
A.音响【3000元,4kg】
B.笔记本电脑【2000元,3kg】
C.吉他【1500元,1kg】
D.一个iphone【2000元,1kg】
这里我就不再演示了,直接给出答案,请同学们自己去学着写写看
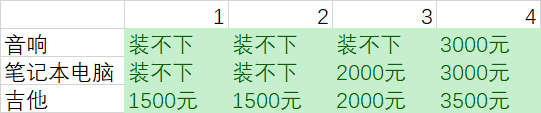
打乱行的顺序
肯定有同学会问,如果我打乱顺序,是否会影响最大价值
这肯定是不会的,那按这种说法岂不是,变成我【先偷吉他后偷电脑】会比【先偷电脑后偷吉他】贵了
也可以给大家演示一下
同学们也可以逐步按列填充,不按行填充,这是一样的
增加一件小商品
如果加入的是项链D.项链【1000元,0.5kg】
那就加大了同学们的负担了,需要做更精细的表格
偷部分商品
比方说我们偷杂货铺,里面有大米,面粉,盐之类的
但这种东西不可能偷全部,因为不可能整袋抗走,不然估计还没出门就被打死了
这个时候不可能用动态规划,而要改用贪心算法
背包没装满
同学们肯定会问,最优解可能导致背包没装满嘛,完全可能
我都不用给大家演示数据,大家想想
五块铁块,和一颗钻石
你的背包又只够装半块铁块的
那你偷什么呢,肯定偷钻石呀
那你装满了吗,没有呀
同学们编程一定要注意不要脱离生活,不然有时候得出来的结论往往容易和卖菜的阿姨都懂的常识相违背