深度学习导论(4)神经网络基础
深度学习导论(4)神经网络基础
- 一. 训练深度学习模型的步骤
- 二. 线性层(或叫全链接层)(Linear layer(dense or fully connected layers))
-
- 1. 定义一个层
- 2. 定义多个层
- 3. 堆叠线性Layers(层)没有意义
- 三. 激活函数
-
- 1. 再谈激活函数
- 2. Sigmoid
- 3. Tanh
- 4. ReLU
- 5. 如何在PyTorch上实现激活函数的调用
- 四. 搭建神经网络模型
-
- 1. torch.nn module
- 2. 基于PyTorch搭建神经网络模型
- 3. 针对不同机器学习问题的模型结构
- 五. Loss function(损失函数)
- 六. Optimizer(优化方法)
- 七. 训练(学习)过程(Training(learning)procedure)
- 八. MNIST-PyTorch实现
-
-
- (1) 代码
- (2) 改变batch并输出input.size
- (3) 改变batch并输出out.size
- (4) 深度学习的本质思想
-
- 九. 计算损失函数
- 十. 更新权重
- 十一. 手写数字识别分类问题具体步骤(Training an handwritten digit classification)
一. 训练深度学习模型的步骤
- 建立数据通道。即把手里的数据预处理成模型输入的形式;
- 搭建神经网络结构模型。即神经网络有几层,每层中有几个神经元,神经元之间是如何连接的;
- 利用损失函数评估模型。输入模型的数据Input经过训练后(例如: 模型中的参数权重矩阵为 w 1 w_1 w1, w 2 w_2 w2,其中 w 1 w_1 w1为第一层与第二层之间连接的权重矩阵, w 2 w_2 w2为第二层与第三层之间连接的权重矩阵,)输出的预测值Output,与输入数据的真实值(即标签Lable)之间的误差,误差的结果就是损失,然后根据误差的值反过来去调整模型中的参数 w 1 w_1 w1与 w 2 w_2 w2,如此反复地进行迭代,一直到找到一组最优(或局部最优)的参数 w 1 w_1 w1与 w 2 w_2 w2。
- 使用优化算法优化神经网络模型权重。在反复迭代的过程中,需要不断地更新 w 1 w_1 w1与 w 2 w_2 w2,这两个矩阵如何更新,就是优化算法。优化算法一般都是基于梯度下降法来更新 w 1 w_1 w1与 w 2 w_2 w2(神经网络有很多优化方法)。

二. 线性层(或叫全链接层)(Linear layer(dense or fully connected layers))
1. 定义一个层
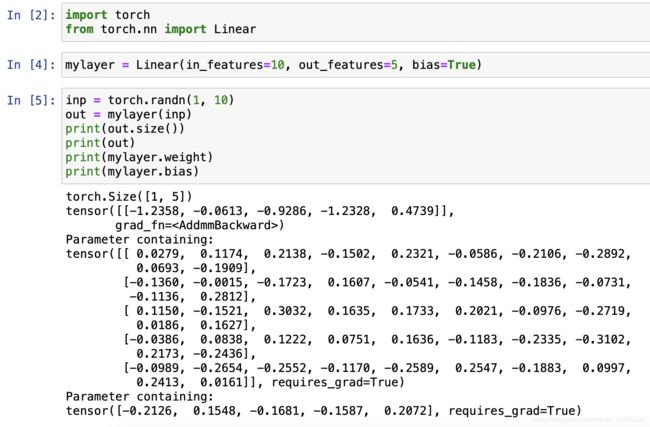
(1) 所有的层的模块都在torch.nn中;
(2) 输入是10个神经元,输出是5个神经元,“bias为指定是否加入偏置项b”;
(3) “inp = torch.randn(1, 10)”表示输入的神经元。其中“1”表示的是batch,即每个批次送入的样本数,“10”表示的是每个batch中每个元素有10个维度;
(4) “out = mylayer(inp)”表示输入层。实际上就相当于一个函数,将输入inp送入到模型中去;
(5) “mylayer.weight”表示权重w。w的矩阵Size为[5, 10]。
注: w为权重矩阵。这里以输入为3个神经元,输出为2个神经元为例。
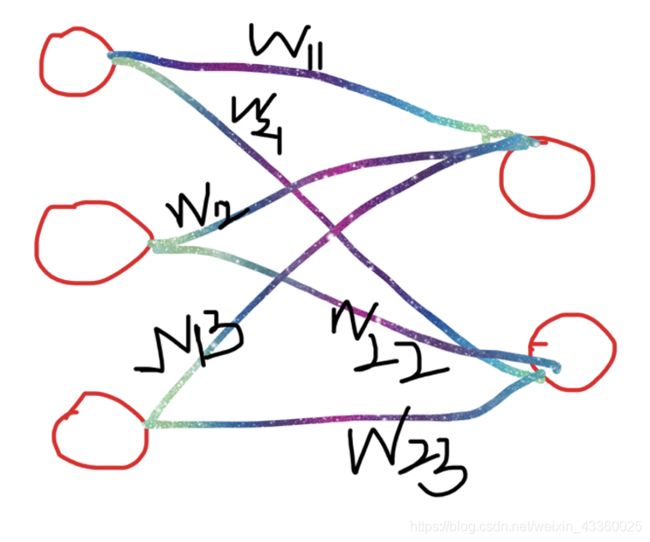
如上图所示,则权重矩阵 w = [ w 11 w 12 w 13 w 21 w 22 w 23 ] w=\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\end{bmatrix} w=[w11w21w12w22w13w23], w w w的维度就是两行三列。
以batch = 3举例,如下:
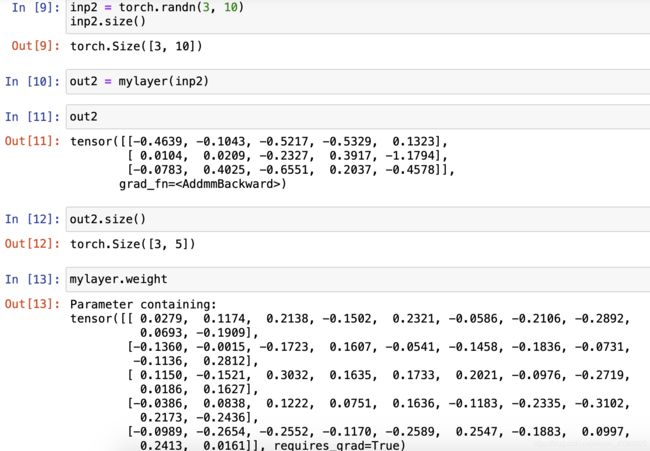
可以发现, w w w权重矩阵并没有改变,这是因为我们没有去更新它。
2. 定义多个层
(1) 第一层输入神经元数量为10,输出神经元数量为5;
(2) 第二层输入神经元数量为5,输出神经元数量为2;
(3) 把第一层作为第二层的输入,这样两个层就串起来了。
神经网络就是这样串起来的,把前一个层的输出作为后一个层的输入。
3. 堆叠线性Layers(层)没有意义
堆叠完后还是相当于一层,只不过权重值由3变为了6,所以堆叠线性层是没有任何意义的,因为权重Weight( w w w)是学习出来的,用两层堆叠起来和直接用一层的效果是一样的。所以我们需要考虑如何将线性层变为非线性层,这就需要引出激活函数。
三. 激活函数
1. 再谈激活函数
- 激活函数可以将线性模型的输出限定在一定的范围内。
- 通过堆叠经过激活函数非线性化后的线性模型,可以高度逼近非线性过程。
- 我们不需要关心用来表示数据的确切的函数类型,只是把深度神经网络模型看做一个通用逼近器或参数估计方法。
- 常用激活函数:
- Sigmoid
- Tanh
- ReLU
- LeakyReLU
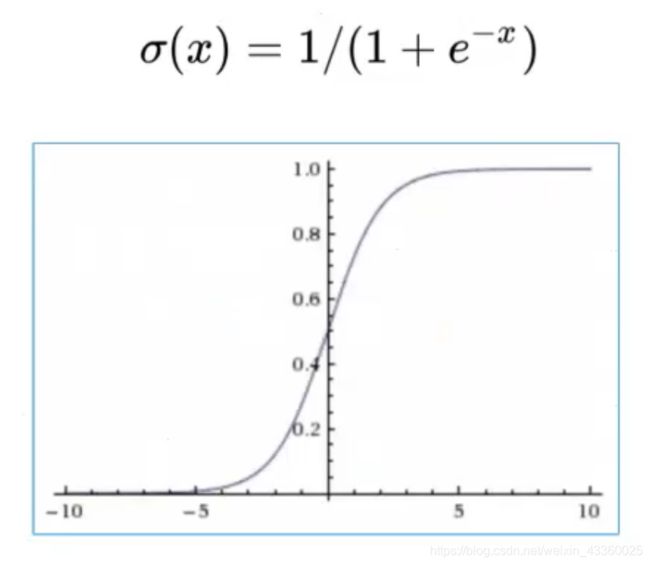
2. Sigmoid
当输入趋近于无穷小时,函数的值就趋近于0; 当输入趋近于无穷大时,函数的值就趋近于1。所以经过Sigmoid激活函数后,输出就压缩到了(0, 1)之间。
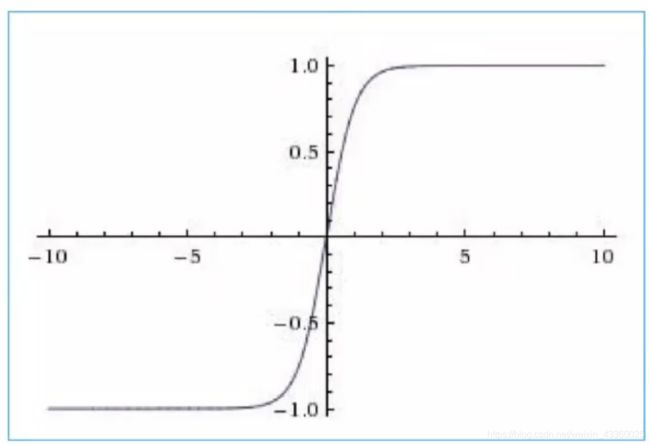
3. Tanh
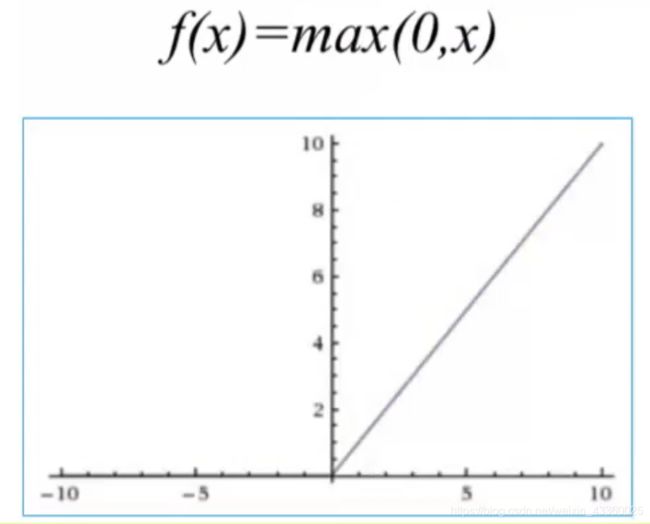
4. ReLU
当输入小于0时,输出等于0; 当输入大于0时,输出等于输入本身。
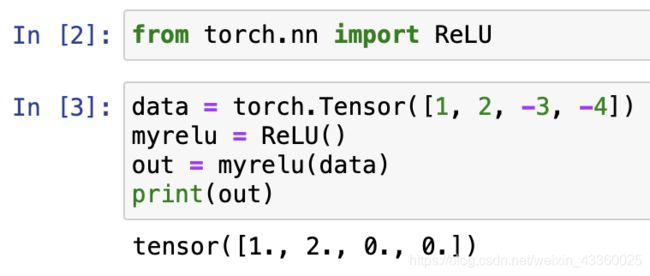
5. 如何在PyTorch上实现激活函数的调用
四. 搭建神经网络模型
1. torch.nn module
- torch.nn module专门用来构建神经网络,其包含了构建所有神经网络结构的模块,在PyTorch中将这些模块成为module(在其他框架中一般成为layers)。
- 所有PyTorch module均继承自torch.nn基类。
2. 基于PyTorch搭建神经网络模型
3. 针对不同机器学习问题的模型结构
- Linear layer: 线性层(一般用于输出层、输入层或中间层)
- Long Short-Term Memory(LSTM): 长短时网络,一种RNN网络(一般用于输入层或中间层)
- CNN: 卷积神经网络(一般用于输入层或中间层)
- The last layer: 输出层
- Linear layer: for regression problem
对于回归问题,一般采用线性层。 - Sigmoid activation function: for binary classification problem
对于二分类问题,一般采用Sigmoid激活函数。 - Softmax layer: for multi-class classification problem
对于多分类问题,一般采用Softmax层。
- Linear layer: for regression problem
举例: 非线性网络可以这样理解: 首先是一些线性层(Linear layer),线性层后边加上非线性层(如ReLU函数),然后ReLU的输出又传送到线性层当中,然后在线性层的后边又加上非线性层(如ReLU函数),…… ,最后加入输出层,输出层要根据任务来决定。
五. Loss function(损失函数)
常用的损失函数:
-
L1 loss: Mostly used as a regularizer.(一般用于正则化或规格化)
-
MSE loss(均方差误差): used as loss function for regression problems(一般用于回归问题中): 1 n ∑ ( Y ^ − Y ) 2 \frac{1}{n}\displaystyle \sum{(\hat{Y}-Y)^2} n1∑(Y^−Y)2其中 Y ^ \hat{Y} Y^为模型预测值, Y Y Y 为真实值。
-
Cross-entropy loss: used for binary and multi-class classfication problems(一般用于二分类或者多分类问题)
对于神经网络模型来说,就是像搭积木一样搭建一个网络模型,再根据具体的任务指定一个损失函数,然后根据损失函数的值去更新模型的权重( w w w和 b b b),这样就能找到一组最优(或者局部最优)的 w w w和 b b b。在搭建神经网络结构的时候,中间到底用几个隐藏层,每一层当中用几个神经元,这些问题就是模型的超参数。
常用的超参数有Learing rate、层数、每层神经元数量等,超参数的设定没有具体原则,就是根据自己数据集的特点或者分布多尝试。
六. Optimizer(优化方法)
如何去更新模型的权重 w w w和 b b b,向左或者向右,每次走多远,怎么去走,这就是优化问题,这也是一种类型的超参数。
常用的优化方法:
- SGD
- Adagrad
- Adam
- RMSProp
一般来说认为Adam比较好用,但是有些问题使用最原始的SGD效果反而更好,需要具体问题具体分析。
七. 训练(学习)过程(Training(learning)procedure)
- Define the neural network that has some learnable parameters(or weights)
- Iterate over a dataset of inputs
- Process input though the network
- Compute the loss(how far is the output from being correct)
- Propagate gradients back into the network’s parameters
- Update the weights of the network,typically using a simple update rule: w e i g h t = w e i g h t − l e a r n i n g _ r a t e ∗ g r a d i e n t weight=weight-learning\_rate*gradient weight=weight−learning_rate∗gradient
- 定义一个神经网络,里边有一些可学习的参数( w w w和 b b b)。可学习的意思就是不需要人为的计算,只需要机器去学习自动帮我们找到最优(或者局部最优)的参数;
- 将数据集作为输入,反复地进行迭代;
- 通过模型进行输入;
- 计算损失值Loss(预测值与真实值之间的误差到底有多大);
- 将梯度传播回模型的参数中(梯度下降法),即根据Loss值去反向的更新模型的权重 w w w和 b b b;
- 一般情况下,使用如下规则去更新 w w w和 b b b: w e i g h t = w e i g h t − l e a r n i n g _ r a t e ∗ g r a d i e n t weight=weight-learning\_rate*gradient weight=weight−learning_rate∗gradient
八. MNIST-PyTorch实现
在输入层前边是没有权重的,即就是原始的输入数据,在输入层和隐藏层之间有权重,在隐藏层和输出层之间有权重,所以对于这个模型,我们需要定义两个层次,而且是两个线性层。
注:
- 在__init__函数中定义模型中的“层”。其中fc1为隐藏层,fc2为输出层。对于fc1层来说,输入就是输入层直接送入模型的数据,即28*28=784维的向量,共有512个神经元; 对于fc2层来说,输入就是前一个层的神经元个数,即512维向量,因为是手写数字识别,共有数字0~9,使用one-hot向量表示lable,所以,输出的神经元有10个。(例如: 0123456789,如果只有“0”上有输出,其它没有,那么输出就是“1000000000”,同理,如果只有“1”上有输出,那么就是“0100000000”)。 在输入层的神经元后有一个SoftMax函数,目的是将神经元的输出概率范围压缩在(0, 1)之间,且所有概率值加起来的和等于1。看概率哪个最大,那么就属于哪一类。(例如,在手写数字识别中,“0”的概率比其他数字都大,那么认为手写数字属于“0”这一类,所以,输出就是“1000000000”)。然后再和样本的真实值作对比得到损失值(例如,这个样本的标签就是“1000000000”,那么这个样本的损失值Loss=0)。
- bias默认为True。
- 一个神经层网络的手写数字识别,其识别正确率就能达到80%~90%,这就是神经网络结构的厉害之处。
- 如果出现“NameError: name ‘nn’ is not defined”,那么需要添加“import torch.nn as nn”。
(1) 代码
代码如下:
import torch
from torch.nn import Linear
import torch.nn as nn
import torch.nn.functional as F
from torch.nn import ReLU
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512)
self.fc2 = nn.Linear(512, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.softmax(self.fc2(x), dim=1)
return x
net = Net()
print(net)
input = torch.randn(1, 28*28)
out = net(input)
print(input)
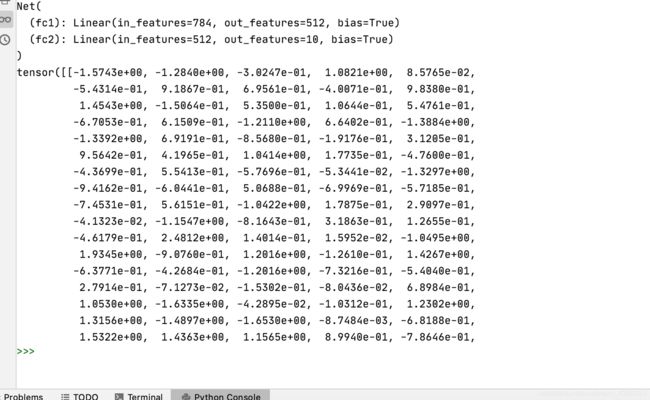
print(out)
其中结果图中上面的tensor为输入,下面的tensor为输出。
注: 在定义forword函数时,如果不加上SoftMax函数,那么输出结果就会有正数也有负数,加上SoftMax函数后,输出结果全部在(0, 1)之间。
(2) 改变batch并输出input.size
将input = torch.randn(1, 28*28)
改为input = torch.randn(2, 28*28)并输出input的size
输出结果如下:

可以看到输入数据的size为(2, 784),其中“2”表示batch,即每一批(batch)将2个样本送进模型; “784”表示每个样本的维度。
(3) 改变batch并输出out.size
将代码改为:
input = torch.randn(200, 28*28)
out = net(input)
print(input.size())
print(out.size())
print(input)
print(out)
输出结果如下:

可以看到输入数据的size为(200, 784),输出数据的size为(200, 10)。
(4) 深度学习的本质思想
通过以上实验可以看出: 深度学习的本质思想就是在做映射,输入到输出之间的映射关系。
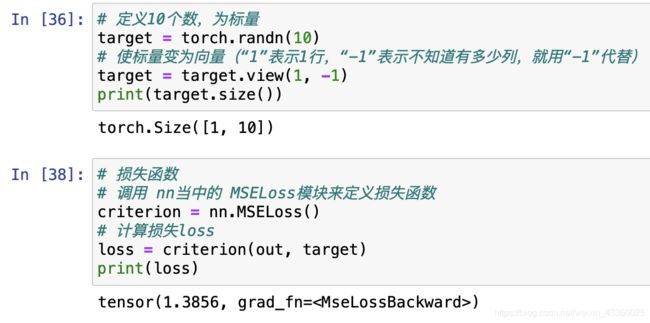
九. 计算损失函数
注: “out”就是模型中的输出,“target”就是模型中的“label”。
十. 更新权重
模型参数(以MNIST-PyTorch实现中的代码为例):
print(net.parameters())
要查看 w w w和 b b b的具体值,需要添加一个迭代器。
十一. 手写数字识别分类问题具体步骤(Training an handwritten digit classification)
- Load and normalizing the MNIST training and test datasets using torchvision;
使用torchvision加载并对MNIST数据集规格化; - Define a Convolution Neural Network
定义卷积神经网络; - Define a loss function
定义损失函数; - Train the network on the training data
利用数据经过反复迭代(多轮epoch),训练网络,得到一组最优的(或者局部最优的)网络参数( w w w和 b b b); - Test the network on the test data
得到网络参数( w w w和 b b b)后,模型就有了,就可以利用测试集数据去测试网络模型。