Vision Transformer原理及代码实战
Vision Transformer原理及代码实战
背景
论文地址:https://arxiv.org/pdf/2010.11929.pdf
代码参考:https://github.com/BR-IDL/PaddleViT
在NLP领域,Transformer深度学习技术已经"统治"了该领域;
在CV领域,从2020年底开始,Vision Transformer(ViT)成为该方向的研究热点;基于Transformer的模型在多个视觉任务中已经超越CNN模型达到SOTA性能的程度;
Transformer概念引入
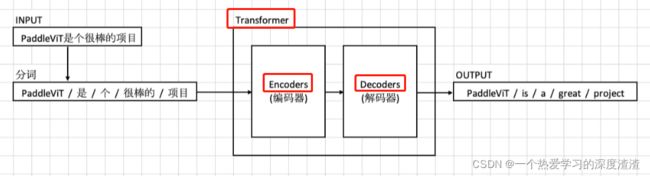
Transform一开始是出现在NLP领域中,下面看一个翻译的实际应用:
主要实现步骤为:
输入文本 —— 分词 —— Transformer模型 —— 输出结果
实际上Encoders和Decoders代表的是多个的组成,类似于卷积网络的堆叠;
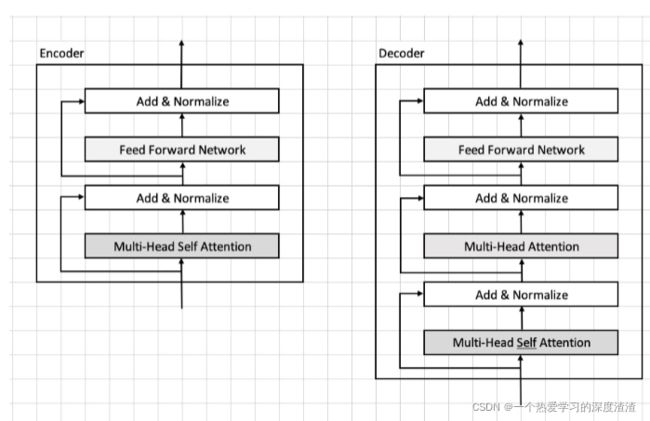
NLP中单独的Encoder和Decoder的具体实现如下:
其中的MSA和FFN结构在后续的代码实战中会进行讲解;
Vision Transformer引入
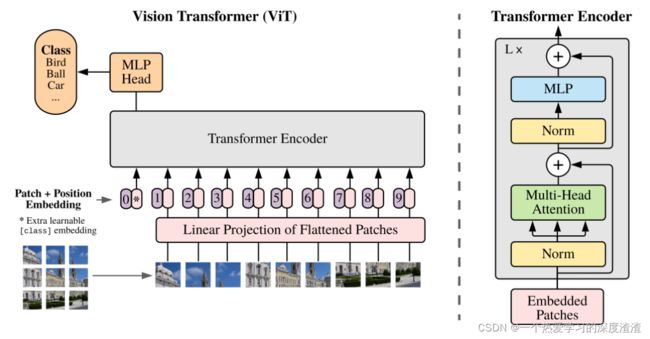
受到NLP领域中Transforms成功应用的启发,ViT算法中尝试将标准的Transformer结构直接应用图图像中,实现流程如下:
1、将整个图像拆分成小图像块;
2、将小图像块映射成线性嵌入序列;
3、将线性嵌入序列传入网络中实现任务;
其中最重要的步骤为Patch Embedding和Encoder,暂时没用到Decoder;
在中规模和大规模的数据集下,作者验证得到以下结论:
1、Transformer对比CNN结构,缺少一定的平移不变性和局部感知性,因此在数据量不够大时,很难达到CNN的同等效果;也就是说在中规模数据集下效果会比CNN的低上几个百分点;
2、当具有大量训练样本时,可使用大规模数据集训练后,再使用迁移学习的方式应用到其他数据集上,此时Transformer可以超越或达到SOTA的水平;
Patch Embedding原理
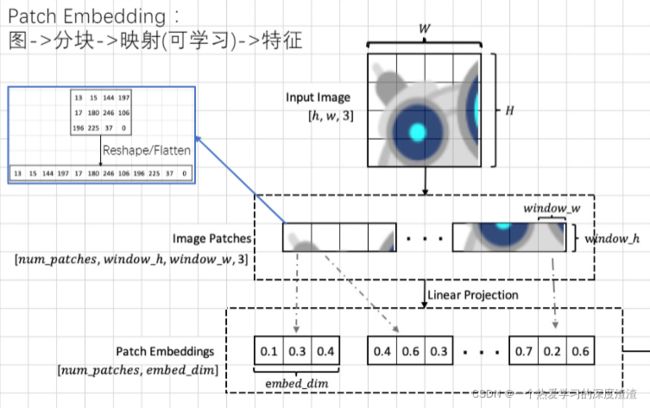
Patch Embedding又称为图像分块嵌入,Transformer结构中,需要输入的是一个二维矩阵(S,D),其中S是sequence的长度,D是sequcence中每个向量的维度,因此需要将三维的图像矩阵转换为二维的矩阵;
ViT中具体的实现方式为,将HWC的图像变成一个S x (P²*C)的序列;其中P代表图像块的边长,C代表通道数,N则表示图像块的个数(WH/P²);由于最终需要的向量维度为D,需要再做一个Embedding的操作,对(P² * C)的图像块做一个线性变化压缩为D即可;
Embedding的定义:高维空间向低维空间的映射;
上面的Patch Embedding也可以通过卷积滑窗来实现(也就是卷积实现)
Attention注意力机制原理
Attention在论文中是这么解释的:在单个序列中使用不同位置的注意力用于实现该序列的表征方法;
最重要的就是提出了query - key - value思想,当时的该模型聚焦的任务主要是question answering,先用输入的问题query检索key-value memories,找到和问题相似的memory的key,计算相关性分数,然后对value embedding进行加权求和,得到一个输出向量,慢慢就衍生了Attention中的qkv;
QKV是输入的X乘上Wq, Wk, Wv三个矩阵得到的;
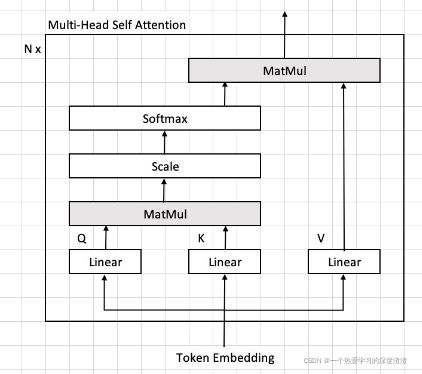
Self Attention的计算图:
结构逻辑图:
代码实现
1、首先实现一下Patch Embedding结构;
class PatchEmbedding(nn.Layer):
def __init__(self, image_size, patch_size, in_channels, embed_dim, dropout=0.):
super().__init__()
# embedding本质是一个卷积操作
self.patch_embedding = nn.Conv2D(in_channels,
embed_dim,
kernel_size=patch_size,
stride=patch_size,
bias_attr=False)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
# x 原来为[n, c, h, w]
x = self.patch_embedding(x) # 经过卷积操作后:[n, c', h', w'],c'是我们所需要的维度
x = x.flatten(2) # 将2、3维度合并:[n, c', h'*w']
x = x.transpose([0, 2, 1]) # 维度转换:[n, h'*w', c']
x = self.dropout(x)
return x
2、实现一个MLP的结构
MLP实际上就是两层全连接,并且经过MLP后维度不发生改变;
class Mlp(nn.Layer):
def __init__(self, embed_dim, mlp_ratio=4.0, dropout=0.):
super().__init__()
# 两层全连接层
self.fc1 = nn.Linear(embed_dim, int(embed_dim * mlp_ratio))
self.fc2 = nn.Linear(int(embed_dim * mlp_ratio), embed_dim)
# GELU的激活函数
self.act = nn.GELU()
# dropout层
self.dropout = nn.Dropout(dropout)
def forward(self, x):
x = self.fc1(x)
x = self.act(x)
x = self.dropout(x)
x = self.fc2(x)
x = self.dropout(x)
return x
3、实现一个Encoder层
class EncoderLayer(nn.Layer):
def __init__(self, embed_dim):
super().__init__()
# 做特征归一化操作
self.attn_norm = nn.LayerNorm(embed_dim)
# Attention层在之后进行实现
self.attn = Attention()
self.mlp_norm = nn.LayerNorm(embed_dim)
# 之前实现的MLP结构
self.mlp = Mlp(embed_dim)
def forward(self, x):
# 这里也有用到残杀结构
h = x
x = self.attn_norm(x)
x = self.attn(x)
x = x + h # 维度不变,可直接相加
h = x
x = self.mlp_norm(x)
x = self.mlp(x)
x = x + h
return x
4、Attention代码实现
class Attention(nn.Layer):
def __init__(self, embed_dim, num_heads,
qkv_bias=False, qk_scale=None, dropout=0., attention_dropout=0.):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.head_dim = int(embed_dim / num_heads)
self.all_head_dim = self.head_dim * num_heads
self.qkv = nn.Linear(embed_dim,
self.all_head_dim * 3,
bias_attr=False if qkv_bias is False else None)
self.scale = self.head_dim ** -0.5 if qk_scale is None else qk_scale
self.dropout = nn.Dropout(dropout)
self.attention_dropout = nn.Dropout(attention_dropout)
self.proj = nn.Linear(self.all_head_dim, embed_dim)
self.softmax = nn.Softmax(-1)
def transpose_multi_head(self, x):
# x:[n, num_patches, all_head_dim]
new_shape = x.shape[:-1] + [self.num_heads, self.head_dim]
x = x.reshape(new_shape)
# x:[n, num_patches, num_heads, head_dim]
x = x.transpose([0, 2, 1, 3])
# x:[n, num_heads, num_patches, head_dim]
return x
def forward(self, x):
B, N, _ = x.shape
# x: [n, num_patches, embed_dim]
qkv = self.qkv(x).chunk(3, -1)
# qkv: [n, num_patches, all_head_dim] * 3
q, k, v = map(self.transpose_multi_head, qkv)
# q, k, v:[n, num_heads, num_patches, head_dim]
attn = paddle.matmul(q, k, transpose_y=True)
attn = self.scale * attn
attn = self.softmax(attn)
attn_weights = attn
attn = self.attention_dropout(attn)
# attn: [n, num_heads, num_patches, num_patches]
out = paddle.matmul(attn, v)
# out: [n, num_heads, num_patches, head_dim]
out = out.transpose([0, 2, 1, 3])
# out: [n, num_patches, num_heads, head_dim]
out = out.reshape([B, N, -1])
out = self.proj(out)
out = self.dropout(out)
return out, attn_weights
由于当前对Attention理解还不够透彻,先把代码粘贴在这,便于之后回顾;
5、实现ViT结构,将之前实现的结构串联到一起
class ViT(nn.Layer):
def __init__(self):
super().__init__()
# 定义Patch Embedding结构
self.patch_embed = PatchEmbedding(224, 7, 3, 16)
# 定义Encoder层
layer_list = [EncoderLayer(16) for i in range(5)]
self.encoders = nn.LayerList(layer_list)
# 定义全连接层实现分类
self.head = nn.Linear(16, 10)
self.avgpool = nn.AdaptiveAvgPool1D(1)
self.norm = nn.LayerNorm(16)
def forward(self, x):
# 第一步经过Patch Embedding(图像分块)
x = self.patch_embed(x) # [n, h*w, c]: 4, 1024, 16
# 第二步进入Transformer层,也就是五层Encoder
for encoder in self.encoders:
x = encoder(x)
x = self.norm(x)
# 进行维度转换
x = x.transpose([0, 2, 1])
# 将所有batch合并起来
x = self.avgpool(x)
x = x.flatten(1)
# 进行分类,输出对应类别的向量
x = self.head(x)
return x
# 用一个主程序进行验证
if __name__ == "__main__":
t = paddle.randn([4, 3, 224, 224])
model = ViT()
out = model(t)
print(out.shape) # 输出[4, 10]
总结
在ViT中我们运用的是LN的标准化处理,而对比BN有什么区别呢,可以参考下面这篇文章:
参考文章:https://www.cnblogs.com/gczr/p/12597344.html
Paddle中还有一个小技巧,就是用paddle.summary可以打印模型的数据流:
paddle.summary(vit, (4, 3, 224, 224)) # must be tuple
打印结果如下图所示:
可以看出每一层的名称,对应的input和output,以及所占用的参数数量;
最后,ViT属于当前比较前沿的技术点,往往对大型数据集有比较好的效果,实际在工作中接触到的数据集没有那么大,加入ViT的结构可能没有很好的效果,反而会影响速度(毕竟有多个Linner层),了解前沿的技术还是有助于我们对网络的选择以及修改的,多学没有坏处!