YOLO V4详解

YOLO V4详细解读

对于V3的改进之处

1、主干特征提取网络：DarkNet53 => CSPDarkNet53

2、特征金字塔：SPP，PAN

3、分类回归层：YOLOv3（未改变）

4、训练用到的小技巧：Mosaic数据增强、Label Smoothing平滑、CIOU、学习率余弦退火衰减

5、激活函数：使用Mish激活函数

1、darknet的改进之处

1.1、在激活函数上采用Mish激活函数

采用了新的激活函数：其一是将DarknetConv2D的激活函数由LeakyReLU修改成了Mish，卷积块由DarknetConv2D_BN_Leaky变成了DarknetConv2D_BN_Mish。
$$Mish=x\ast tanh(ln(1+e^2))$$

1.2、在整体的结构上改变

yoloV3在整体的结构上Darknet53采用一些列的残差结构进行堆叠，而V4在整个darkNet中采用的是一个大的CSP结构：

CSPnet结构并不算复杂，就是将原来的残差块的堆叠进行了一个拆分，拆成左右两部分：
主干部分继续进行原来的残差块的堆叠；
另一部分则像一个残差边一样，经过少量处理直接连接到最后。
因此可以认为CSP中存在一个大的残差边。

1.3增加了SPP结构

主要是用来解决不同尺寸的特征图如何进入全连接层的，直接看下图，下图中对任意尺寸的特征图直接进行固定尺寸的池化，来得到固定数量的特征。

如上图，以3个尺寸的池化为例，对特征图进行一个最大值池化，即一张特征图得取其最大值，得到1d(d是特征图的维度)个特征；对特征图进行网格划分为2x2的网格，然后对每个网格进行最大值池化，那么得到4d个特征；同样，对特征图进行网格划分为4x4个网格，对每个网格进行最大值池化，得到16*d个特征。 接着将每个池化得到的特征合起来即得到固定长度的特征个数（特征图的维度是固定的），接着就可以输入到全连接层中进行训练网络了。用到这里是为了增加感受野。

2、三种不同尺寸的预测

如图这是V4的整体结构，跟V3是一样的，有三个部分。

输出层的shape分别为(19,19,75)，(38,38,75)，(76,76,75)，最后一个维度为75是因为该图是基于voc数据集的，它的类为20种，YoloV4只有针对每一个特征层存在3个先验框，所以最后维度为3x25；

3、预测结果

由第二步我们可以获得三个特征层的预测结果，shape分别为(N,19,19,255)，(N,38,38,255)，(N,76,76,255)的数据，对应每个图分为19x19、38x38、76x76的网格上3个预测框的位置。

在yoloV3中，我们会得到3个特征层分别将整幅图分为19x19、38x38、76x76的网格，每个网络点负责一个区域的检测。

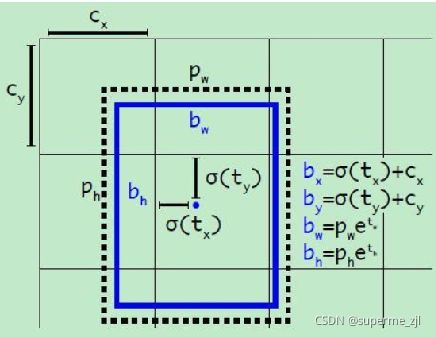
yolo3的解码过程就是将每个网格点加上它对应的x_offset和y_offset，加完（这里的加是指的是anchor中的中心网格点坐标（Cx，Cy））后的结果就是预测框的中心，然后再利用 先验框和h、w结合 计算出预测框的长和宽。这样就能得到整个预测框的位置了。

当然得到最终的预测结构后还要进行得分排序与非极大抑制筛选
这一部分基本上是所有目标检测通用的部分。

对于yoloV4不过该项目的处理方式与其它项目不同。其对于每一个类进行判别。

1、取出每一类得分大于self.obj_threshold的框和得分。
2、利用框的位置和得分进行非极大抑制。

2、YOLOV4的改进训练技巧

1、Mosaic数据增强

每次随机读取四张图片，分别对四张图片进行反转，缩放，色域变化等，并且按照四个方向位置摆好。

mosaic操作这增强了对正常背景(context)之外的对象的检测，丰富检测物体的背景。此外，每个小批包含一个大的变化图像(4倍)，因此，减少了估计均值和方差的时需要大mini-batch的要求，降低了训练成本。

2、DropBlock正则化

yolo4采用了dropblock正则化，有助于避免过拟合的问题。

过拟合：模型在训练集上表现很好，但在测试集上却表现很差。模型对训练集"死记硬背"（记住了不适用于测试集的训练集性质或特点），没有理解数据背后的规律，泛化能力差。

DropBlock方法的引入是为了克服Dropout随机丢弃特征的主要缺点，Dropout被证明是全连接网络的有效策略，但在特征空间相关的卷积层中效果不佳。DropBlock技术在称为块的相邻相关区域中丢弃特征。这样既可以实现生成更简单模型的目的，又可以在每次训练迭代中引入学习部分网络权值的概念，对权值矩阵进行补偿，从而减少过拟合

3、Label Smoothing平滑

其实Label Smoothing平滑就是将标签进行一个平滑，原始的标签是0、1，在平滑后变成0.005(如果是二分类)、0.995，也就是说对分类准确做了一点惩罚，让模型不可以分类的太准确，太准确容易过拟合。

4、CIOU值

$$IOU=\frac{area(C)\cap area(G)}{area(C)\cup area(G)}$$
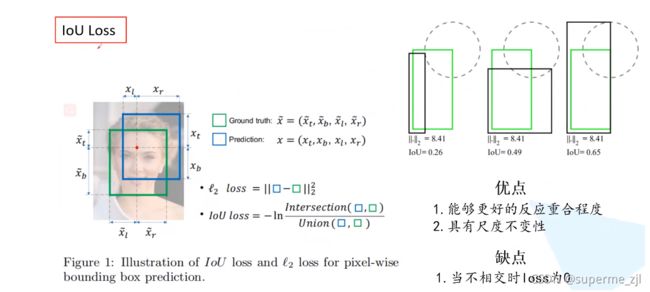
在YoloV3中IOU损失是采用了一个差值平方的计算方法：

其中Iou loss的计算方式，-ln(iou) 也可以表示为1-Iou

GIou loss

其中绿色是框是真实框，红色是预测框，蓝色是用一个最小的矩形将两个框框在一起，其中
$$\begin{gathered} A^c=蓝色的面积 \\ u=两个框并集的面积 \end{gathered}$$
Giou大部分是优秀于IOU的，但是在特定情况下会退化成IOU当真实框和预测框在等高等宽时，会变成普通的IOU

对于DIou

由上图中，第一行是Giou在400轮迭代后才勉强预测到跟真实框差不多的

而第二行是Diou的仅仅只用了120次迭代就跟真实框差不多了，所以DIou相对于Giou要提升了许多，具体DIou的计算公式是

$$\begin{gathered} b=黑色是预测框目标的中心点 \\ {b}^{gt}=绿色是真实框的中心点 \\ {p}^2=两个中心点的距离平方 \end{gathered}$$
Diou损失能直接最小化两个框之间的距离，因此可以收敛的速度更快。

对于CIou

其中这个Ciou考虑了3种几何参数：重叠面积，中心点的距离，长宽比。

把1-CIOU就可以得到相应的LOSS了。

5、对于学习率的调整问题

余弦调度会根据一个余弦函数来调整学习率。首先，较大的学习率会以较慢的速度减小。然后在中途时，学习的减小速度会变快，最后学习率的减小速度又会变得很慢。

上升的时候使用线性上升，下降的时候模拟cos函数下降。执行多次。

相当于一个余弦函数的调整策略

2、loss组成

a)、计算loss所需参数
在计算loss的时候，实际上是y_pre和y_true之间的对比：
y_pre就是一幅图像经过网络之后的输出，内部含有三个特征层的内容；其需要解码才能够在图上作画
y_true就是一个真实图像中，它的每个真实框对应的(19,19)、(38,38)、(76,76)网格上的偏移位置、长宽与种类。其仍需要编码才能与y_pred的结构一致
实际上y_pre和y_true内容的shape都是
(batch_size,19,19,3,85)
(batch_size,38,38,3,85)
(batch_size,76,76,3,85)

b)、y_pre是什么
网络最后输出的内容就是三个特征层每个网格点对应的预测框及其种类，即三个特征层分别对应着图片被分为不同size的网格后，每个网格点上三个先验框对应的位置、置信度及其种类。
对于输出的y1、y2、y3而言，[…, : 2]指的是相对于每个网格点的偏移量，[…, 2: 4]指的是宽和高，[…, 4: 5]指的是该框的置信度，[…, 5: ]指的是每个种类的预测概率。

c)、y_true是什么。
y_true就是一个真实图像中，它的每个真实框对应的(19,19)、(38,38)、(76,76)网格上的偏移位置、长宽与种类。其仍需要编码才能与y_pred的结构一致

d)、loss的计算过程
在得到了y_pre和y_true后怎么对比呢？不是简单的减一下!

loss值需要对三个特征层进行处理，这里以最小的特征层为例。
1、利用y_true取出该特征层中真实存在目标的点的位置(m,19,19,3,1)及其对应的种类(m,19,19,3,80)。
2、将prediction的预测值输出进行处理，得到reshape后的预测值y_pre，shape为(m,19,19,3,85)。还有解码后的xy，wh。
3、对于每一幅图，计算其中所有真实框与预测框的IOU，如果某些预测框和真实框的重合程度大于0.5，则忽略。
4、计算ciou作为回归的loss，这里只计算正样本的回归loss。
5、计算置信度的loss，其有两部分构成，第一部分是实际上存在目标的，预测结果中置信度的值与1对比；第二部分是实际上不存在目标的，在第四步中得到其最大IOU的值与0对比。
6、计算预测种类的loss，其计算的是实际上存在目标的，预测类与真实类的差距。

其实际上计算的总的loss是三个loss的和，这三个loss分别是：

实际存在的框，CIOU LOSS。
实际存在的框，预测结果中置信度的值与1对比；实际不存在的框，预测结果中置信度的值与0对比，该部分要去除被忽略的不包含目标的框。
实际存在的框，种类预测结果与实际结果的对比。

参考原文链接：https://blog.csdn.net/weixin_44791964/article/details/106214657

https://space.bilibili.com/18161609/channel/seriesdetail?sid=244160