基于Pytorch的神经网络之Optimizer

目录

1.引言

2.各种优化器

2.1 SGD

2.2 Momentum

2.3 RMSprop

2.4 Adam

3.效果对比

---

1.引言

我们之前提到进行反向传播时我们需要用到优化器(Optimizer)来优化网络中的参数，优化器有许多种，下面介绍几种常见的优化算法。

2.各种优化器

2.1 SGD

优化算法中比较基本的一种就是随机梯度下降法(SGD),它通过从全部样本中选取一部分样本计算梯度(使函数下降最快的方向向量)，在其中随机选取一个梯度来下降，依据此来调整参数的值，由于其期望值与普通梯度下降一致，所以它最终也能收敛，只是过程略显曲折。

优点：

1. 将大批量数据分为小规模数据计算梯度值，加快了收敛速度，训练速度更快。
2. 对梯度要求低，能够较好应对噪声干扰。

缺点：

1. 引入噪声，使每一步下降不一定全局最优(走偏路)。

2.2 Momentum

SGD的一种改进便是动量优化法(Momentum)，它引入了类似物理中的动力的概念，使每一次优化过程受上一次优化的正向干扰，就像小球滚的时候具有惯性一样。

优点：

1. 减小了噪声的影响和收敛的曲折程度。
2. 收敛速度更快。

2.3 RMSprop

RMSprop算法也可以看成是对SGD的一种改进算法，它可以根据历史梯度修正学习率，在大梯度时增大学习率，小梯度时减小学习率。

优点：

1. 学习率拥有适应性，避免学习率越来越低。
2. 在非凸情况下效果更好

2.4 Adam

Adam可以粗略看成是Momentum和RMSprop的结合，将两者的优势相结合产生的更好的算法。也是使用者较多的一种深度学习优化算法。

优点：

1. 鲁棒性好(可以简单理解为对环境的适应性强，万金油)。
2. 训练速度通常更快

3.效果对比

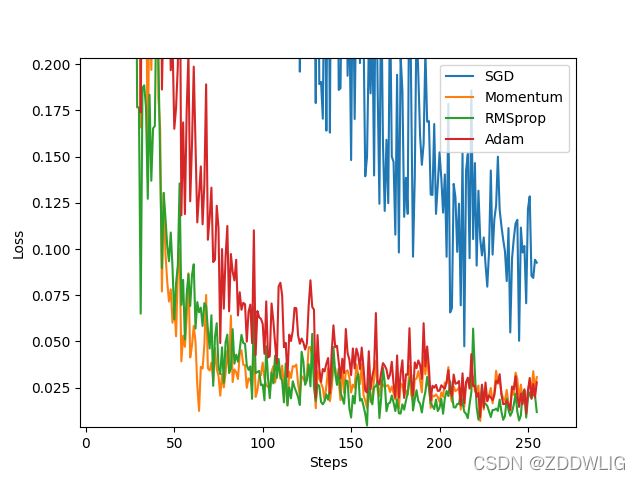
下面是在用神经网络进行回归时四种优化算法的效果对比：

 我们可以看到SGD明显不如其余三种算法：速度慢而且误差大，其余三种算法loss基本一致，速度相差也并不很大。

 下面是代码，大家可以直接试试看。

#调包
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

#定义超参数
LR = 0.01
BATCH_SIZE = 32
EPOCH = 8

#制作数据
x = torch.unsqueeze(torch.linspace(-2, 2, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

#构建网络
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

if __name__ == '__main__':
    #分四次训练
    net_SGD         = Net()
    net_Momentum    = Net()
    net_RMSprop     = Net()
    net_Adam        = Net()
    nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
    
    #四个不同的优化器
    opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
    opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
    opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
    opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
    optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
    
    #定义损失函数
    loss_func = torch.nn.MSELoss()
    losses_his = [[], [], [], []]  
    
    #开始训练
    for epoch in range(EPOCH):
        print('Epoch: ', epoch)
        for step, (b_x, b_y) in enumerate(loader):       
            for net, opt, l_his in zip(nets, optimizers, losses_his):
                output = net(b_x)              
                loss = loss_func(output, b_y) 
                opt.zero_grad()               
                loss.backward()                
                opt.step()                     
                l_his.append(loss.data.numpy())   
    
    #绘图可视化
    labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
    for i, l_his in enumerate(losses_his):
        plt.plot(l_his, label=labels[i])
    plt.legend(loc='best')
    plt.xlabel('Steps')
    plt.ylabel('Loss')
    plt.ylim((0, 0.2))
    plt.show()