机器学习基础整理(第五章) - 分类器的性能评估和改进
文章目录
- 总览
- 评估 (Assessment)
-
- 整体思路
- 判别性
-
- Holdout 估计 (留出法)
- 交叉验证 (Cross Validation)
- Bootstrap 技术
- 可靠性
- ROC
-
- 二分类ROC规则
- 模型的比较
-
- 统计测试 (statistical test)
- ROC 比较
- 分类器组合 (Combining Classifiers)
-
- 多分类器系统 (multiple classifier systems) 的架构
-
- 不同的特征空间 (Different feature spaces)
- 公共特征空间 (Common feature space)
- 重复测量 (Repeated Measurements)
- 分类器合成方法
-
- 乘积规则 (Product Rule)
- 累加规则 (Sum Rule)
- 多数投票法 (Majority Vote)
- 多专家模型 (Mixture of experts)
- Bagging (Boostrap Aggregating)
- Boosting
总览
性能问题有两方面: 评估 (assessment) 以及 提升 (improvement)。
评估与在设计阶段优化参数不同。
在进行评估时,我们还对 几个分类器在性能方面之间的比较 感兴趣。
如果我们能知道如何评估分类器的性能,我们是否可以将多个分类器的输出组合起来以提高性能呢?
评估 (Assessment)
整体思路
我们需要考虑三方面:
- 分类器在未知数据中表现得多好?- 判别性 (Discriminability)
- 分类器对类成员的后验概率的估计效果如何?- 可靠性 (Reliability)
- 我们如何使用 接受者操作特征 (Receiver Operating Characteristic - ROC) 作为性能的指示?
判别性
基本的思想就是根据可用数据来估计错误率 (error rate)。
错误率的缺点在于它是一个单一的性能度量,不会为 错误分类 (misclassifications) 和正确分类分配不同的权重。
混淆矩阵 (Confusion Matrix) 通常与错误率结合使用,以帮助显示错误的分布。
用于估计错误率的方法包括:
- Holdout estimate
- Cross-validation 交叉验证
- Jackknife
- Bootstrap技术
让 Y = { y i , i = 1 , . . . , n } Y=\{y_i, i = 1, ..., n\} Y={yi,i=1,...,n} 代表训练数据。
每一个 y i y_i yi 是一个分割向量 (partitioned vector) y i t = [ x i t z i t ] y_i^t = [x_i^t \space \space \space z_i^t] yit=[xit zit]
其中 { x i , i = 1 , . . . , n } \{x_i, i = 1, ..., n\} {xi,i=1,...,n} 是 衡量 (measurement) (或 模式向量 pattern vector),而 { z i , i = 1 , . . . , n } \{z_i, i = 1, ..., n\} {zi,i=1,...,n} 是对应的标签。
当 x i ∈ ω j x_i \in \omega_j xi∈ωj 的时候, ( z i ) j = 1 (z_i)_j = 1 (zi)j=1。否则,等于 0 0 0。
ω ( z i ) \omega(z_i) ω(zi) 是对应的分类类别标签。
决策规则: η ( x ; Y ) ⇒ \eta(x;Y) \Rightarrow η(x;Y)⇒ 基于 Y Y Y 将 x x x 分配给 类 η \eta η 的分类器。
定义一个损失函数, Q ( . ) Q(.) Q(.):

各种不同类型的误差衡量:
- 表观错误率 (apparent error rate) (或 重新代换率 resubstitution rate) 是通过使用 设计集 估计错误率得到的。
- 真实错误率 (true error rate, e T e_T eT) 是错误分类随机选择的模式向量的 预期概率 (expected probability),在从与训练数据相同的分布中抽取 无限大测试集 (infinitely large test set) 上计算出来的。
- 预期错误率 (expected error rate e E e_E eE) 是 给定大小的测试集 上真实错误的预期值。
Holdout 估计 (留出法)
基本思想是将可用数据分成两个互斥的集合:
- 训练集
- 测试集
分类器是使用训练集和在独立集上评估的性能 设计的。
问题: 数据使用率低下,估计存在悲观偏差。
对于 真实错误率 e t e_t et, n n n 个独立测试样本中 k k k 个 错误分类样本(misclassfied samples or errors) 的概率为:

交叉验证 (Cross Validation)
这个方法也被称为 U方法 (U-method),留一法 (leave-one-out),或删除估计 (deleted estimates)。
误差用以下方式计算:
- 在设计或训练集 获得 n − 1 n - 1 n−1 个样本。
- 在剩余那个样本上进行测试 。
- 对大小为 n − 1 n − 1 n−1 的所有 n n n 个子集 进行 重复计算。
估计值近似无偏 (unbiased),代价是估计量的方差增加 (increased variance)。
若 Y j Y_j Yj 是 删除了 观测点 x j x_j xj 的训练集,其交叉验证误差是:
e C V = 1 n ∑ i = 1 n Q ( ω ( z j ) , η ( x j , Y j ) ) e_{CV}=\frac{1}{n}\sum_{i=1}^nQ(\omega(z_j), \eta(x_j, Y_j)) eCV=n1i=1∑nQ(ω(zj),η(xj,Yj))
v-折叠 交叉验证 (v-fold cross validation)
v-fold 交叉验证的轮换方法 (rotation method) 将训练集划分为 v v v 个子集,在 v − 1 v-1 v−1 上训练并在剩余集上测试。
Bootstrap 技术
该方法包括对观察到的分布进行采样 (sampling) 和替换 (replacement),以生成可用于 校正偏差 (correct for bias) 的观察集。
随机选取数据并允许重复,这被称为 “Sampling With Replacement”
Bootstrap 偏差校正 的表观误差为:
e A ( B ) = e A − W b o o t e_A^{(B)}=e_A - W_{boot} eA(B)=eA−Wboot
其中 W b o o t W_{boot} Wboot 是 bootstrap 偏差。
让数据以以下方式表示, Y = { [ x i t z i t ] t , i = 1 , . . . , n } Y = \{[x_i^t \space \space z_i^t]^t, i = 1, ..., n\} Y={[xit zit]t,i=1,...,n}
使 F ‾ \overline{F} F 作为 经验分布 (empirical distribution),
估算误差的流程是:
- 生成一组新数据 (bootstrap样本)
Y b = { [ x i t z i t ] t , i = 1 , . . . , n } Y^b = \{[x_i^t \space \space z_i^t]^t, i = 1, ..., n\} Yb={[xit zit]t,i=1,...,n} - 使用 Y b Y^b Yb 设计分类器。
- 在样本上 计算 表观误差率 e ‾ A \overline{e}_A eA
- 计算 分类器的 实际误差率 e ‾ C \overline{e}_C eC (此时将 Y Y Y 视为总体)
- 计算 w b = e ‾ A − e ‾ C w_b = \overline{e}_A - \overline{e}_C wb=eA−eC
- 重复上述步骤,一共 B B B 次。
- Boostrap 偏差的表观误差率等于 W b o o t = E [ w b ] = 1 B ∑ b = 1 B w b W_{boot} = E[w_b] = \frac{1}{B} \sum_{b=1}^Bw_b Wboot=E[wb]=B1∑b=1Bwb
- Boostrap 偏差校正 的表观误差率 是 e A ( B ) = e A − W b o o t e_A^{(B)} = e_A - W_{boot} eA(B)=eA−Wboot
可靠性
这是 规则估计 类别所属的 后验概率 的衡量标准。
以下情况,后验值很重要:
- 将根据成本做决定。
- 分类器的结果将用于进一步的分析阶段。
可能的 不精确度量 (measure of imprecision) 如下,
将经验样本统计量 与其 使用分类函数计算的估计值 p ‾ ( ω i ∣ x ) \overline{p}(\omega_i|x) p(ωi∣x) 进行比较。

其中若 x i ∈ ω j x_i \in \omega_j xi∈ωj, 则 z j i = 1 z_{ji} = 1 zji=1,否则是0。函数 ϕ j \phi_j ϕj 可以是 1 − p ‾ ( ω j ∣ x j ) 2 1 - \overline{p}(\omega_j|x_j)^2 1−p(ωj∣xj)2
ROC
二分类ROC规则
在 ROC 图像中,TP被画在 Y轴上,而 FP 被画在 X轴上。
每个具有 指定类分布 和 成本矩阵 的分类器都 表示为 ROC 空间中的一个点 ( F P , T P ) (FP, TP) (FP,TP)。
如果 ROC X X X 总在 ROC Y Y Y 的上方和左侧,则 X X X 强于 Y Y Y,这意味着 X X X 分类器 在所有可能的错误成本和类分布中 始终具有比 Y Y Y 更低的预期成本。
比如图中, A A A 和 B B B 强于 D D D。
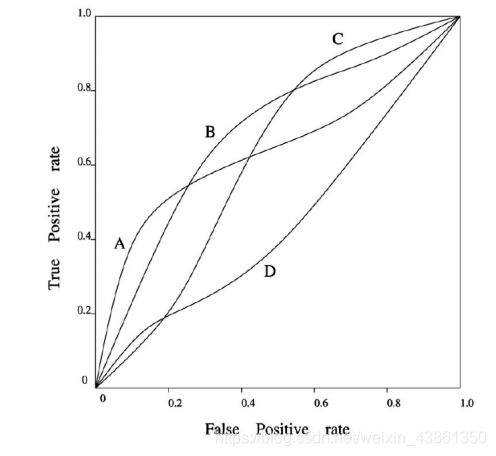
ROC A A A 和 B B B 在整个范围内都没有相互支配,我们如何比较它们?
当 类分布 和 错误成本 未知时,我们使用 ROC 曲线下的面积 (area under the ROC) 来比较两个分类器。
AUC 定义: AUC (Area under the curve 曲线下面积) 表示 随机选择的负例 比 随机选择的正例 具有 更小的 估计概率属于正类 的概率。
设我们拥有两个类别 ω i , i = 1 , 2 \omega_i, i=1, 2 ωi,i=1,2 以及一个估计 属于类别的样本的后验概率 p ( ω i ∣ x ) p(\omega_i|x) p(ωi∣x) 的分类器。
设 估计为 { f 1 , . . . , f n 1 ; f i = p ( ω 1 ∣ x ) , x ∈ ω 1 } \{f_1, ..., f_{n1}; f_i = p(\omega_1|x), x \in \omega_1\} {f1,...,fn1;fi=p(ω1∣x),x∈ω1}。同样地,使得 { g 1 , . . . , g n 2 ; g i = p ( ω 2 ∣ x ) , x ∈ ω 2 } \{g_1, ..., g_{n2}; g_i = p(\omega_2|x), x \in \omega_2\} {g1,...,gn2;gi=p(ω2∣x),x∈ω2},其中 n 1 n1 n1 和 n 2 n2 n2 分别是 在类别 ω 1 \omega_1 ω1 和 ω 2 \omega_2 ω2 中 测试样本的数量。
以升序 (increase order) 排序 估计集 { f 1 , . . . , f n 1 , g 1 , . . . , g n 2 } \{f_1, ..., f_{n1}, g_1, ..., g_{n2}\} {f1,...,fn1,g1,...,gn2} 以及使 从 ω 1 \omega_1 ω1 的 第 i i i 个模式的排序 为 r i r_i ri。
研究者 表明随机选择的类 ω 2 ω_2 ω2 模式比随机选择的类 ω 1 ω_1 ω1 模式具有更低的属于类 ω 1 ω_1 ω1 的估计概率的概率估计是:

S 0 S_0 S0 是 类 ω 1 \omega_1 ω1 测试模式 排序 的总和。 A ‾ \overline{A} A 和 AUC 是相等的。
例子,
让下面的表格代表 模式估计的后验概率 的排序表:

则其AUC计算如下:
模型的比较
分类器性能因数据集,样本大小,数据维度而异。
我们需要考虑进行比较的基础: 错误率,可靠性和速度等。
在进行比较的时候,需要排除分析人员的技能,因为通常根据分析人员的专业程度使得需要优化的分类器有不同的性能。
比较 的主要问题是: “给定两个分类器和足够的独立训练数据,哪个分类器在新的测试集示例上更准确?”
统计测试 (statistical test)
McNemar’s or Gillick 测试 尝试回答: “当不存在差异时,错误检测分类器性能差异的概率是多少?”
对于两个分类器, A A A 和 B B B,我们的定义如下:
n 00 = n_{00}= n00= A A A 和 B B B 都 分类错误 的样本数
n 01 = n_{01}= n01= A A A 分类错误 但 B B B 没出错 的样本数
n 10 = n_{10}= n10= A A A 没出错 但 B B B 分类错误 的样本数
n 11 = n_{11}= n11= A A A 和 B B B 都 没有分类错误 的样本数
统计 z z z 通过下式计算:

其中 z 2 z^2 z2 的分布如同 以一个自由度 的 X 2 X^2 X2 。
如果 ∣ z ∣ > 1.96 |z| \gt 1.96 ∣z∣>1.96, 则可以 拒绝分类器具有 相同错误 的零假设 (null hypothesis) (错误拒绝的概率为 0.05)
ROC 比较
在这个例子,我们比较两个分类器 A A A 和 B B B。同时我们提供错误率以及AUC。模式估算的后验概率排序列表如下表格:

AUC按照下式计算

A U C ( A ) = 24 25 AUC(A) = \frac{24}{25} AUC(A)=2524 而 A U C ( B ) = 16 25 AUC(B) = \frac{16}{25} AUC(B)=2516,而对应的表观误差为 e A ( A ) = 2 10 e_A(A)=\frac{2}{10} eA(A)=102 而 e A ( B ) = 2 10 e_A(B)=\frac{2}{10} eA(B)=102
分类器组合 (Combining Classifiers)
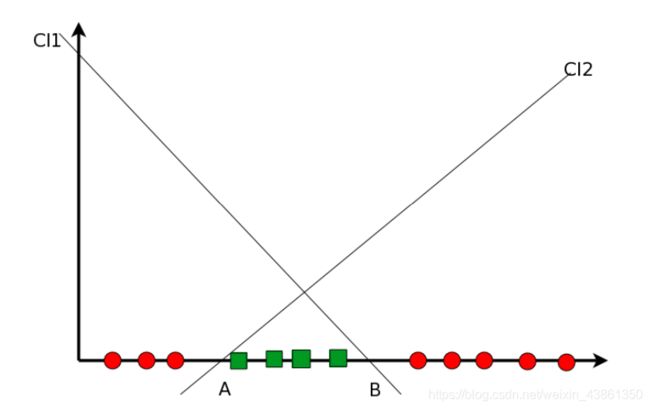
上图是在单变量数据 (univariate) 上定义的两个 线性判别式 (linear discriminants)
多分类器系统 (multiple classifier systems) 的架构
不同的特征空间 (Different feature spaces)
每个 组件分类器 (component classifier) 都是针对不同的特征设计的。 每个分类器提供后验概率的估计。 示例 多模态分类 (multi-modal classification),最佳的 组合规则 是什么?

上图表示 在不同特征空间上定义的组件分类器。
公共特征空间 (Common feature space)
每个 组件分类器 都定义在 相同的特征空间上,组合器 (combiner) 尝试获得更好的分类器。 分类器可以 不同或相似 (dissimilar or similar) (不同的训练集 或 不同的初始化)。给定 组合规则 的 最佳组件分类器 是什么?
重复测量 (Repeated Measurements)
同一个组件分类器被输入 连续的测量值 (successive measurements) 并且 决定 被组合起来。 这也称为 时间融合 (temporal fusion) 或 多观测融合 (multiple observation fusion)。 示例是使用 步态 (gait) 连续识别一个人。

上图表示 在公共特征空间中 被提供时间分离的测量值 (temporally seperated measurements) 的分类器。
分类器合成方法
设我们拥有一个 需要被分类的 对象 Z Z Z,还有 L L L 个 分类器,其输出为 x 1 , . . . , x L x_1, ..., x_L x1,...,xL
根据贝叶斯最小误差法则, Z Z Z 被分配到 类 ω j \omega_j ωj 若以下条件满足
p ( ω j ∣ x 1 , . . . , x L ) > p ( ω k ∣ x 1 , . . . , x L ) , k = 1 , . . . , L ; k ≠ j p(\omega_j | x_1, ..., x_L) \gt p(\omega_k|x_1, ..., x_L), k=1, ..., L; k\ne j p(ωj∣x1,...,xL)>p(ωk∣x1,...,xL),k=1,...,L;k=j
或同等地, Z Z Z 被分配到 类 ω j \omega_j ωj 若以下条件满足
p ( x 1 , . . . , x L ∣ ω j ) p ( ω j ) > p ( x 1 , . . . , x L ∣ ω k ) p ( ω k ) , k = 1 , . . . , L ; k ≠ j p(x_1, ..., x_L | \omega_j)p(\omega_j) \gt p(x_1, ..., x_L|\omega_k)p(\omega_k), k = 1, ..., L; k \ne j p(x1,...,xL∣ωj)p(ωj)>p(x1,...,xL∣ωk)p(ωk),k=1,...,L;k=j
当然,我们需要 类条件联合概率密度 (class-conditiona joint probability densities) 的知识,即 p ( x 1 , . . . , x L ∣ ω j ) , j = 1 , . . . , L p(x_1, ..., x_L|\omega_j), j = 1, ..., L p(x1,...,xL∣ωj),j=1,...,L
乘积规则 (Product Rule)
如果我们假设 条件独立 (conditional independence),则分配规则变为乘积规则。
将 Z Z Z 分配给 类 ω j \omega_j ωj,若:

或根据单个分类器的后验概率,将 Z Z Z 分配给 类 ω j \omega_j ωj,若:

化简得到:

累加规则 (Sum Rule)
若我们假设 在 δ k i ≪ 1 \delta_{ki} \ll 1 δki≪1 的情况下, p ( ω k ∣ x i ) = p ( ω k ) ( 1 + δ k i ) p(\omega_k | x_i) = p(\omega_k) (1 + \delta_{ki}) p(ωk∣xi)=p(ωk)(1+δki),这种情况下乘积规则中使用的后验概率与先验偏差不大,我们可以推导出 累加规则。
将 Z Z Z 分配给 类 ω j \omega_j ωj,若:

化简得到:

多数投票法 (Majority Vote)
通常应用于生成 唯一类标签 (unique class labels) 作为输出并且不需要训练的分类器。
将此规则应用于 产生后验概率 作为输出的分类器 需要在 输出处应用 二元函数以将 p ( ω k ∣ x k ) p(\omega_k|x_k) p(ωk∣xk) 替换为 Δ k i \Delta_{ki} Δki
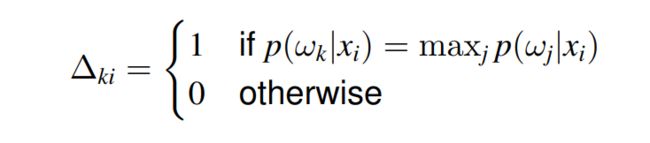
模式被分类到 组件分类器 最常预测 (most often predicted) 的类别,并 通过选择具有 最大先验概率 (largest prior probability) 的类别来解决平局。
多专家模型 (Mixture of experts)
一种 训练多个 组件分类器 (专家 experts) 和 组合器 (门控函数 gating function) 以提高性能的学习过程。 类似于 “累加规则”,但该方法会有 训练 步骤。
每个专家的输出 是 输入 x x x 的广义线性函数:
o i ( x ) = f ( w i t x ) o_i(x) = f(w_i^tx) oi(x)=f(witx)
其中 w i w_i wi 是关联 第 i i i 个专家 的 权重向量,而 f ( . ) f(.) f(.) 是一个固定的连续非线性函数。
门控网络 是一个 广义线性函数 g g g:
g i ( x ) = g ( x , v i ) = e x p ( v i t x ) ∑ k = 1 L e x p ( v i t x ) g_i(x) = g(x, v_i) = \frac{exp(v_i^tx)}{\sum_{k=1}^Lexp(v_i^tx)} gi(x)=g(x,vi)=∑k=1Lexp(vitx)exp(vitx)
输出形成 专家输出的 权重 v i , i = 1 , . . . , L v_i, i=1, ..., L vi,i=1,...,L
总输出为:
o ( x ) = ∑ k = 1 L g k ( x ) o k ( x ) o(x) = \sum_{k=1}^Lg_k(x)o_k(x) o(x)=k=1∑Lgk(x)ok(x)
Bagging (Boostrap Aggregating)
这是一种组合 从同一个数据集中生成的分类器 的做法。
训练集的副本 是通过 bootstrap采样 (bootstrap sampling) 生成的,每个分类器都在每个副本上进行训练。
每个分类器应用于每个 模式 X X X 以及通过 多数投票法 确定的类别。
本质上,bootstrap采样 (从大小为 n n n 的数据集中进行 n n n 次) 替换产生 B 个 bootstrap 数据集 Y Y Y,每个数据集大小为 n n n。
最终分类器的输出是子分类器最常预测的类。
Bagging 对于不稳定的分类器 (unstable classifers) 很有用 - 数据集的小变化会导致预测的大变化。
Boosting
Boosting 是一种 “提升” 弱分类器 (weak classifiers) 性能的做法 (弱分类器即参数估计通常不准确且性能不佳的分类器)
它是非确定性的,根据前一次的迭代结果生成训练集和分类器。
Boosting 为训练集中的每个模式分配一个权重 以 反映其重要性,分类器是基于训练集 和 分配的权重构建的。




