吴恩达深度学习第二课第二周作业及学习心得体会——minibatch、动量梯度下降、adam

概述

学习课程后，在L2正则化代码的基础上完成该周作业，现将心得体会记录如下。

Mini-batch梯度下降

概念

对m个训练样本，每次采用t（1

具体过程为：将特征X分为T个batch，每个batch的样本数为t（最后一个batch样本数不一定为t）。相应的将标签Y也如此分为T个batch。然后在每次训练时，原本是对所有样本进行一次训练；该算法则是对T个batch都进行训练，因此每次训练完所有样本，实际上都进行了T次训练。

注意为了保证没批样本的一致性，在分批前应对样本进行序号进行洗牌，随机重新分配样本的序号。

实际实现时，通常将每个batch的样本数t设置为2的整数次幂（64，128，256…）这是为了节省计算机内存。

理解

不用这种方法时：

执行一次梯度下降，向量化运算需要处理所有样本，耗时长；

当处理一次所有样本时，执行了一次梯度下降。

采用批量梯度下降算法时：

执行一次梯度下降，向量化运算需要处理t个样本，耗时短；

当处理一次所有样本时，执行了T次梯度下降。

因此可知，当样本量大时，其优点显而易见！假设有1000000个样本，如果不采用批量梯度下降法，用了20000次训练（即20000次梯度下降），才得到合适的网络；如果采用批量梯度下降法，令t=1000（则T=1000000/1000=1000），则每次训练完所有样本，实际上已经执行了1000次梯度下降，如果样本在分批时进行了随机排序处理，那么在上面的假设条件下，只需要对所有样本进行20次训练（梯度下降次数=20×1000=20000），就可以找到合适的网络。其效率明显提高。

特殊情况

当t=m（总样本数）时，等于没有分批，称作批梯度下降。

优点：最小化所有训练样本的损失函数，得到全局最优解；易于并行实现。

缺点：当样本数目很多时，训练过程会很慢。

当t=1时，每次只对一个样本进行训练，称作随机梯度下降。

优点：训练速度快。

缺点：最小化每条样本的损失函数，最终的结果往往是在全局最优解附近，不是全局最优；不易于并行实现。

代码更改

代码更改如下：

• 增加分批函数：

def random_batch(X, Y, batch_size):
    batchs = []
    np.random.seed(0)
    m = X.shape[1]
    random_index = list(np.random.permutation(m))   #random_index为一维数组，大小0~m-1，顺序随机
    shuffled_X = X[:,random_index]                  #对X按照random_index的顺序重新排序（洗牌）
    shuffled_Y = Y[:,random_index]                  #对Y按照random_index的顺序重新排序（洗牌）
    num_batchs = int(np.floor(m/batch_size))        #计算批数
    
    for k in range(0,num_batchs):                   #将洗牌后的X,Y分成num_batchs个batch
        start = k * batch_size
        end = (k+1) * batch_size
        batch_X = shuffled_X[:,start:end]
        batch_Y = shuffled_Y[:,start:end]
        batch = (batch_X, batch_Y)
        batchs.append(batch)
    if m % batch_size != 0:                         #如果总样本数不能整分，将剩余样本组成最后一个batch
        start = (k+1) * batch_size
        end = m
        batch_X = shuffled_X[:,start:end]
        batch_Y = shuffled_Y[:,start:end]
        batch = (batch_X, batch_Y)
        batchs.append(batch)   
    
    return batchs

• 模型函数：

def NN_model(X, Y, layer_dims, learning_steps, learning_rate, lambd, batch_size, print_flag):
    costs=[]
    batchs = random_batch(X, Y, batch_size)                 #将样本以batch_size分为一组batch
    K = len(batchs)                                         #batchs长度
    parameters =  init_para(layer_dims)                     #初始化参数
    for i in range(0, learning_steps):                      #进行learning_steps次训练
        for k in range(0, K):
            x = batchs[k][0]                                #第k个batch的特征
            y = batchs[k][1]                                #第k个batch的标签
            AL, caches, L2_SUM = prop_forward(x, parameters,lambd)  #前向传播，计算A1~AL
            cost = compute_cost(AL,y,L2_SUM)                #计算成本
            grads = prop_backward(AL, y, caches, lambd)     #反向传播，计算dW1~dWL,db1~dbL
            parameters = update_para(parameters, grads, learning_rate)  #更新参数
        if print_flag==True and i%100==0:
            print('cost at %i steps:%f'%(i, cost))
            costs.append(cost)
    return parameters,costs

实施效果

总样本数为5000，参数如下：

layer_dims = [X.shape[0],4,2,1]     #NN的规模
steps = 1000                        #训练次数
rate = 0.1                          #训练步长
print_flag = True                   #打印cost标识
lambd = 0                           #L2正则化系数，为0时不进行正则化

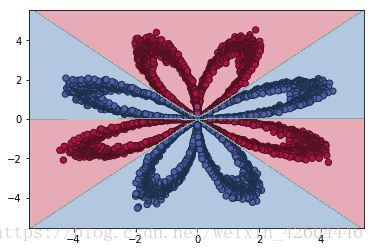
令batch_size=m，效果如下。

令batch_size=512，效果如下。

可见分批处理后，收敛速度明显变快！

动量梯度下降

概念

动量梯度下降（Gradient Descent with Momentum）是计算梯度的指数加权平均数，并利用该值来更新参数值。具体过程为：

其中的动量衰减参数β一般取0.9。

进行一般的梯度下降将会得到图中的蓝色曲线，而使用Momentum梯度下降时，通过累加减少了抵达最小值路径上的摆动，加快了收敛，得到图中红色的曲线。

当前后梯度方向一致时，Momentum梯度下降能够加速学习；前后梯度方向不一致时，Momentum梯度下降能够抑制震荡。

代码更改

在保留上面代码的基础上更改，代码更改如下：

增加初始化函数：

def init_v(parameters): 
    L = len(parameters)//2          #NN层数
    v = {}
    
    for l in range(L):
        v["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
        v["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
        
    return v

更新参数函数：

def update_para(parameters, grads, v, learning_rate):
    L = len(parameters)//2
    beta = 0.9                          #动量梯度下降系数（梯度的指数加权平均系数）
    for l in range(L):
        v["dW" + str(l+1)] = beta*v["dW" + str(l+1)]  + (1- beta)*grads["dW" + str(l+1)]
        v["db" + str(l+1)] = beta*v["db" + str(l+1)]  + (1- beta)*grads["db" + str(l+1)]
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v["db" + str(l+1)]     
    return parameters, v

实施效果

总样本数为5000，参数如下：

layer_dims = [X.shape[0],4,2,1]     #NN的规模
steps = 1000                        #训练次数
rate = 0.1                          #训练步长
print_flag = True                   #打印cost标识
lambd = 0                           #L2正则化系数，为0时不进行正则化
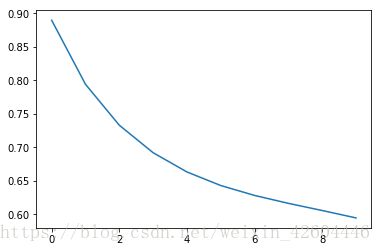
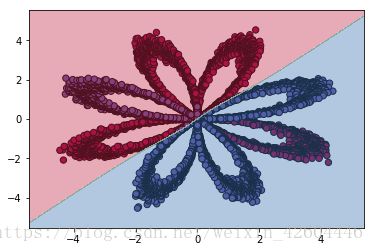
batch_size = 512                    #mini_batch_size，为1时即为随机梯度下降，为X.shape[1]时即不分批

令beta=0.9，预测准确率为0.975200，效果如下。

令beta=0，预测准确率为0.970600，效果如下。

可能是样本过于简单，使用动量梯度下降时除了准确率略微提高，并没有明显变化。

Adam优化算法

概念

Adam(Adaptive Moment Estimation，自适应矩估计)优化算法适用于很多不同的深度学习网络结构，它本质上是将Momentum梯度下降和RMSProp算法结合起来。具体过程为：

其中的学习率α需要进行调参，超参数β1被称为第一阶矩，一般取0.9，β2被称为第二阶矩，一般取0.999，ϵ一般取10^−8。

代码更改

在2.4代码的基础上更改，代码更改如下：

增加初始化函数：

def init_adam(parameters): 
    L = len(parameters)//2          #NN层数
    v = {}
    s = {}
    
    for l in range(L):
        v["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
        v["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
        s["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
        s["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
        
    return v,s

更新参数函数：

def update_para(parameters, grads, v, s, learning_rate):
    L = len(parameters)//2
    v_corrected = {}
    s_corrected = {}
    t=2                     #t不能为0！
    beta1=0.9
    beta2=0.999
    epsilon=1e-8
    for l in range(L):
        v["dW" + str(l+1)] = beta1*v["dW" + str(l+1)]  + (1- beta1)*grads["dW" + str(l+1)]
        v["db" + str(l+1)] = beta1*v["db" + str(l+1)]  + (1- beta1)*grads["db" + str(l+1)]

        v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)]/(1-beta1**t)
        v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/(1-beta1**t)

        s["dW" + str(l+1)] = beta2*s["dW" + str(l+1)]  + (1- beta2)*(grads['dW' + str(l + 1)]**2)
        s["db" + str(l+1)] = beta2*s["db" + str(l+1)]  + (1- beta2)*(grads['db' + str(l + 1)]**2)

        s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/(1-beta2**t)
        s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-beta2**t)

        parameters['W' + str(l+1)] = parameters['W' + str(l+1)] - learning_rate*v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)
        parameters['b' + str(l+1)] = parameters['b' + str(l+1)] - learning_rate*v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)

    return parameters, v, s

实施效果

总样本数为5000。采用adam算法，参数如下。

layer_dims = [X.shape[0],4,2,1]     #NN的规模
steps = 100                         #训练次数
rate = 0.01                         #训练步长
print_flag = True                   #打印cost标识
lambd = 0                           #L2正则化系数，为0时不进行正则化
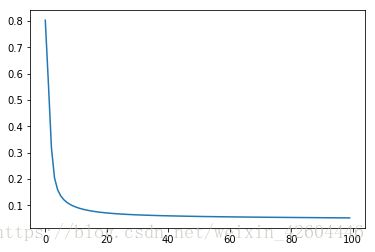
batch_size = 512                    #mini_batch_size，为1时即为随机梯度下降，为X.shape[1]时即不分批

步长减至0.01，训练次数减至100，即可得到合适的网络，效果如下（每10次全样本训练记录一次cost）。

同样的参数，使用动量梯度下降时100次全样本训练后并未收敛，效果如下（每10次全样本训练记录一次cost，注意左下图纵轴范围0.6~0.9）。

可见同样的参数时，adam的收敛速度快很多！

总结

从上面的分析和试验，可知上述措施能够有效的优化神经网络，令神经网络训练时可以更快收敛。

附

相关代码可以在我的资源中下载！希望能帮到大家！