二分查找 & 二分答案 万字详解,超多例题,带你学透二分。
很多人对二分感到很苦恼,很困惑,可能是因为二分的边界很难掌握,也许是判断条件难写…
然而,很幸运,你找到了这篇文章,仔细看下去,这篇文章将带你学透二分!!!
二分可以简单分为二分查找与二分答案。
可能你听说过二分查找,二分查找和二分答案是不是一回事呢?答案是否定的。二分查找只是单纯的查找就可以了,简单的控制好边界条件。而二分答案也许稍复杂些。
首先,我们看一下二分的模板:
模板1:
while (l < r)
{
int mid = l + r >> 1; //(l+r)/2
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
模板2:
while (l < r)
{
int mid = l + r + 1 >> 1; //(l+r+1)/2
if (check(mid)) l = mid;
else r = mid - 1;
}
看到这,以后的你就不会因为边界问题而困惑了!!!
第一个模板是尽量往左找目标,第二个模板是尽量往右找目标。
只要是往左找答案,就用第一个模板,mid不用加一,r=mid,l加一;
只要是往右找答案,就用第二个模板,mid要加一,l=mid,r要减一;
二分套这两个模板,肯定没错!(只要判断条件写对)亲测有效!!!
下面的题目更能证明这句话!
这两个模板一定要牢牢记住哦
当然,二分可能在实数中进行,那自然少不了浮点二分。
模板3:(浮点二分)
while(r-l>1e-5) //需要一个精度保证
{
double mid = (l+r)/2;
if(check(mid)) l=mid; //或r=mid;
else r=mid; //或l=mid;
}
浮点二分就相对简单多了,因为浮点除法不会取整,所以mid,l,r,都不用加1或减1.
我们先来学二分查找:
二分查找也称折半查找,顾名思义,就是每次查找去掉不符合条件的一半区间,直到找到答案(整数二分)或者和答案十分接近(浮点二分)。
光说不练假把式,来个例题:
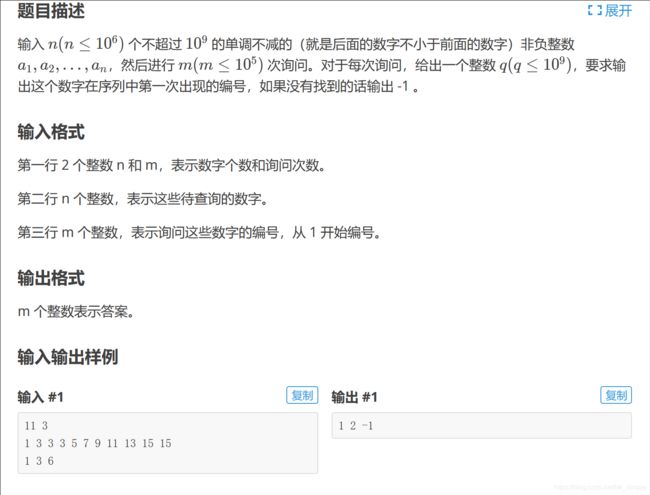
例题1——查找
首先,区间是有单调性的,查找第一次出现的位置,如果查到一个值比目标值大,就把右半边放弃,因为右半边肯定也比目标值大;同样,如果查到值比目标值小,那就放弃左半边。
本文的所有例题都有分析,题解,并注上详细注释。先自己尝试一下,再看题解哦。
code:
#include有一个小问题就是,如果找不到这个值(即,集合里没有这个数)怎么办?因为判断条件是大于等于目标值,那返回的就是第一个大于目标值的位置。
好了,现在的你已经进入了二分世界的大门,此时让我们畅游吧!
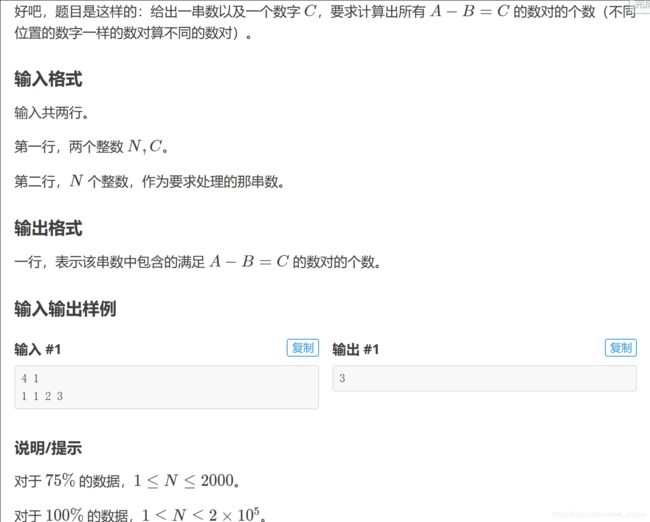
例2——A-B 数对
分析:给出了C,我们要找出A和B。我们可以遍历数组,即让每一个值先变成B,然后二分找对应的A首次出现位置,看是否能找到。
如果找到A,那就二分找最后出现的位置,继而,求出A的个数,即数对的个数。
code:
#include如果你把上面的两个题完全搞懂了,那很容易就抽象出做题步骤:
如果题目明确说了 要求最小值(最前面的值)还是求最大值(最后面的值),就能判断是用模板1(求最小),还是用模板2(求最大)。
之后再根据模板1,或模板2,写出对应的判断条件;
但是,我们不建议死记模板,更重要的是在理解之后的灵活变通。比如,再看一个题。
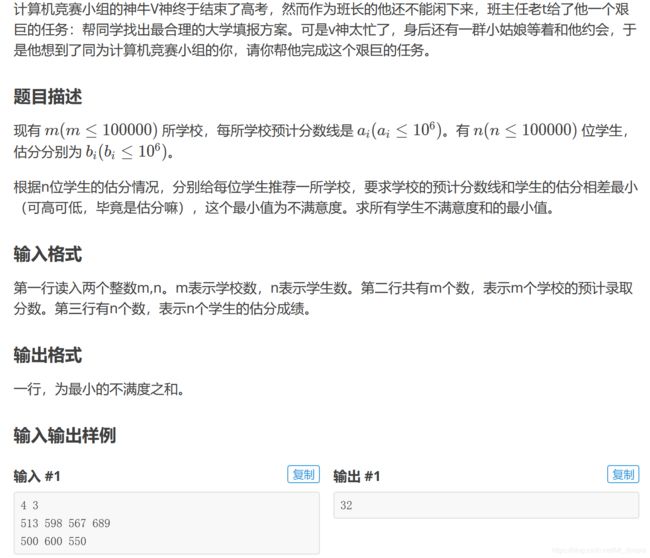
例3——烦恼的高考志愿
分析:这题,就需要稍微理解一下下。
要求估分和分数线相差最小,那肯定分数线刚超过估分或者估分刚超过分数线。我们就转化为,求第一个大于等于估分的分数线的位置。
如此,这个位置的分数线或前一位置的分数线就是和估分相差最小的。
code:
#include此外,STL中还有两个二分函数:lower_bound 和 upper_bound;具体可以看这个博客;或这个(有很多大佬总结的知识点都很好,有啥不懂的话都可以翻博客)
有了这两个函数,我们就可以很方便的求出第一个大于(或等于)目标值的位置;于是,上面代码的中间可以这样改:
while(m--)
{
cin>>x;
int t=lower_bound(a+1,a+n+1,x)-a; //如果分数线都比估分低,那返回的位置是n+1,否则返回第一个大于等于估分的位置。
if(a[t]-x<=x-a[t-1]) sum+=a[t]-x;
else sum+=x-a[t-1];
}
是不是简洁多了?
最后,我们再来看一个浮点二分:
例4——银行贷款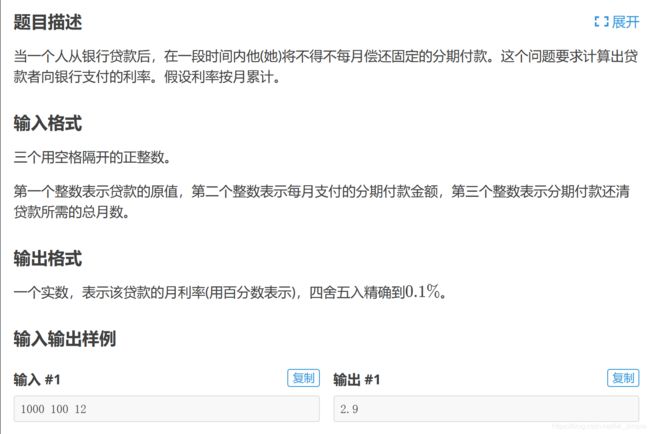
分析:对于月利率,大几率是小数,那么,我们就需要浮点二分。
月利率的范围可以放大些,比如,0~500,然后从这个范围里查,直到和答案极度相近,终止。 最后的l或r,精确位数之后就是正确✔答案啦!
code:
#include至此,相信你已经对二分查找有一个更加清晰的认识了。
课后再来几个练习题吧:
整数二分:
1、 数的范围
2、 砍树
实数二分:
3、 数的三次方根
4、 一元三次方程求解
学会了二分查找,来学二分答案!
首先:
二分查找与二分答案有何区别?
二分查找:在一个已知的有序数据集上进行二分地查找
二分答案:答案有一个区间,在这个区间中二分,直到找到最优答案
什么是二分答案?
答案属于一个区间,当这个区间很大时,暴力超时。但重要的是——这个区间是对题目中的某个量有单调性的,此时,我们就会二分答案。每一次二分会做一次判断,看是否对应的那个量达到了需要的大小。
判断:根据题意写个check函数,如果满足check,就放弃右半区间(或左半区间),如果不满足,就放弃左半区间(或右半区间)。一直往复,直至到最终的答案。
其实,上面二分查找的例4,寻找的那个区间就是答案区间。
这不就相当于高中做选择题的时候,完了,不会做,那咋搞,把四个选项代进去看看对不对吧!哪个行得通那个就是答案!!
只不过我们现在要找的是最大的或者最小的答案。
如何判断一个题是不是用二分答案做的呢?
1、答案在一个区间内(一般情况下,区间会很大,暴力超时)
2、直接搜索不好搜,但是容易判断一个答案可行不可行
3、该区间对题目具有单调性,即:在区间中的值越大或越小,题目中的某个量对应增加或减少。
此外,可能还会有一个典型的特征:求...最大值的最小 、 求...最小值的最大。
1、求...最大值的最小,我们二分答案(即二分最大值)的时候,判断条件满足后,尽量让答案往前来(即:让r=mid),对应模板1;
2、同样,求...最小值的最大时,我们二分答案(即二分最小值)的时候,判断条件满足后,尽量让答案往后走(即:让l=mid),对应模板2;
先看一个经典的二分答案入门:
例1——木材加工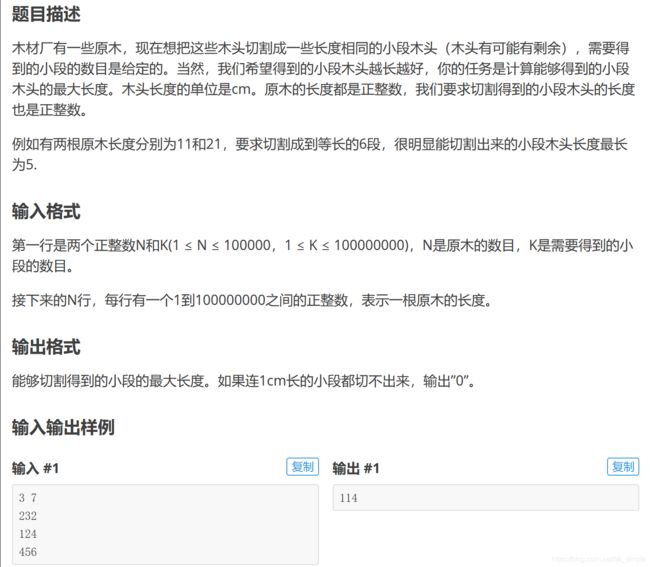
分析:看,答案就在区间(1,100000000)里,就等着我们找呢,暴力肯定超时,那可能就用二分。
满足条件:
1,答案在一个区间里。
2,如果给一个答案,给目标一个小段的长度,很容易判断是否到K个了。
3,具有单调性,目标小段越长,那能切出的段数越少,目标小段越短,能切出的段数越多。而最终需要K个,从而很容易判断一个答案行不行。一看求啥,求最长长度,最长?这不,关门打狗,模板2! !
那,判断条件?模板2,如果满足判断,l=mid。啥叫满足呢?那肯定是满足需要的段数了呗!
code:
#include是不是感觉很有意思?
再来看个经典的
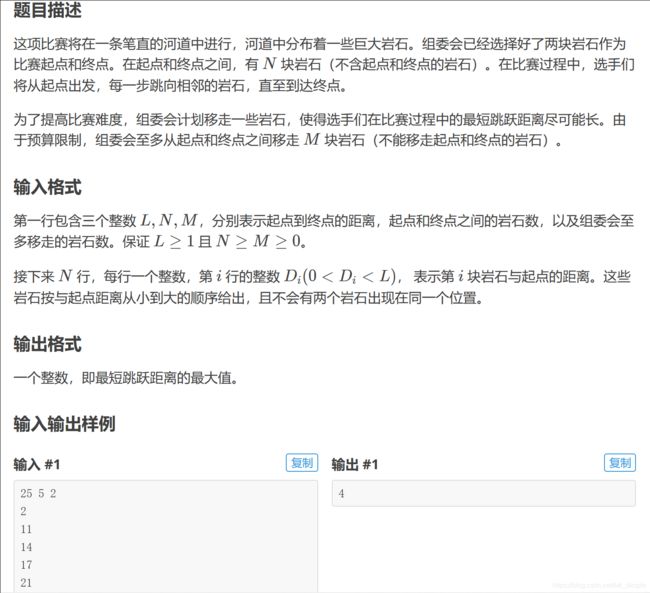
例2——跳石头
分析:看题,这是啥?最短距离的最大值!这不就是二分答案的典型特征?还想啥,二分!
求最大?上模板2!! 那,判断条件?
这时候就要注意了,我们二分的是最短距离,通过二分将这个最短距离(答案)最大化。那我们判断的时候肯定要保证mid是最短距离。
如何保证?我们要求抽过石头剩下的石头中,两个石头间的最短距离为mid,那就要保证剩下的任意两个间距都要大于等于mid。要保证这个,那就只能挑间距大于等于mid的石头跳,中间的石头都将会被抽走。
最后,计数可以被抽走的石头。如果可以被抽走的石头个数小于等于需要抽的M个了,就说明满足条件。因为:既然抽了小于M个都能满足剩下的石头中,两石头间的距离都大于等于mid了,那抽M个,更能满足!
有点晕?没关系!看了代码就懂了!
code:
#include还没懂?没关系,我们再看一题!
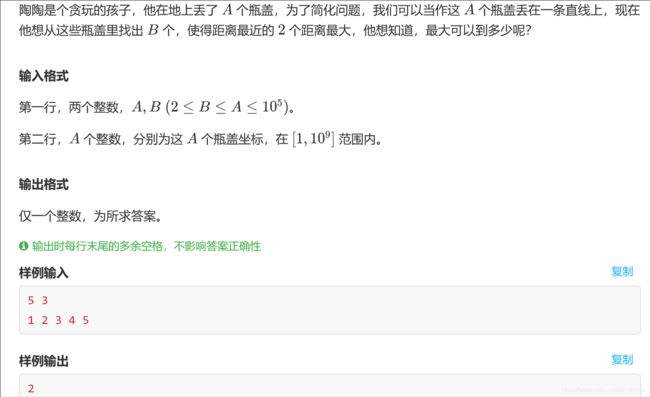
例3——丢瓶盖
分析:距离最近的2个瓶盖距离最大? 最短距离的最大值! 二分!!
看——求最大值,模板二!
判断条件check:与上题不同的是,这题是保证拿走的那些瓶盖之间的最短距离最大(上题是保证剩下的石头最短距离最大,这两个容易混淆。是我没错了… ),那么,遍历的时候,只要满足这次和上次拿的那个瓶盖间距大于等于mid,就可以拿了。这样就保证了我们找的最短距离mid是最短的间距。
最后如果拿出的总瓶盖数大于等于目标值,就说明满足判断。因为:既然拿了超过目标值就能满足拿走的瓶盖间距大于等于mid,那拿目标值(B)个,肯定更能满足!
code:
#include做了上面两题,我们差不多又可以总结出规律了,心里是不是有点小激动?
最大值最小,最小值最大 类 问题解题方向:
最短距离最大化问题:保证任意区间距离要比最短距离mid大或相等(这样,mid才是最短距离)即:区间的距离>=mid
最长距离最小化问题:保证任意区间距离要比最大距离mid小或相等(这样,mid才是最大距离)即:区间的距离<=mid
哈哈哈,是不是太有趣啦?
快快,趁热打铁,再来!!
例4——数列分段 Section II

 分析:没错,这次是最大值最小!
分析:没错,这次是最大值最小!
求最小值? 哎对,模板1!
判断条件:要保证:每一段的和都小于等于最大值。也就是说,只要这一段的和加上下一个值大于最大值了,那下一个值加不得,得分段!接着段数++;
最后,统计出的总段数(cnt+1)小于等于目标值了,那就算满足;因为,既然分了小于目标值个段都能保证每段的和小于等于最大值,那么分目标值个段肯定还能保证!
还有一个小细节:l,和 r 的初始化。
所有段中的最大和肯定大于等于数列中的最大值(因为最大值最少单成一段,那所有段中的最大的和肯定要大于等于最大值),所以l要初始化为maxa。
同样,所有段中和的最大值,最大不过数列中的所有值的和。
code:
#include好啦,至此,二分答案你就差不多掌握了。方法说的都是实打实的;
最后,在给出几道练习题吧:
1、进击的奶牛
2、路标设置
3、最佳牛围栏
4、kotori的设备
本文的课后练习题的答案在这个博客里。
相信看到这的你一定收获了不少吧。
讲的有点多,看不完的话可以先收藏。如果有没讲到的,后续会再更新。
有哪里不明白的话欢迎留言或评论,相互讨论,共同进步!
哪里写的有问题的话,还请大佬们不吝赐教。
参考博客:https://www.it610.com/article/1292865348768440320.htm