RF2O激光里程计算法源码解析与相关公式推导

---

  很早之前看过这篇论文，但是当时还是以多线激光雷达为主，最近又回到了2D激光里程计，所以有重新看了这部分代码，顺便记录一下！
之前的原理部分可参考：RF2O激光里程计算法原理

1.CMakeLists 起飞

先从 CMakeLists 开始看 ～

find_package(catkin REQUIRED COMPONENTS  
  roscpp
  rospy
  nav_msgs
  sensor_msgs
  std_msgs
  tf  
)
find_package(Boost REQUIRED COMPONENTS system)
find_package(cmake_modules REQUIRED)
find_package(Eigen REQUIRED)
find_package(MRPT REQUIRED base obs maps slam)

  因为后面是打算去 ROS 的，所以比较关注工程的依赖，这里也就一个 tf ，看起来应该比较容易， 还有一个陌生的库 MRPT ，在官网中是这样介绍的：

  移动机器人编程工具包 (MRPT) 是一个广泛的、跨平台的开源 C++ 库，旨在帮助机器人研究人员设计和实施（主要）在同步定位和建图 (SLAM)、计算机视觉和运动规划（避障）。优点是代码的效率和可重用性。
  这些库用于轻松管理 3D(6D) 几何的类、许多预定义变量（点和位姿、路标、地图）的概率密度函数 (pdf)、贝叶斯估计（卡尔曼滤波器、粒子滤波器）、图像处理、路径规划和障碍物躲避，所有类型的地图（点，栅格地图，路标，…）等的 3D 可视化。
  高效地收集、操作和检查非常大的机器人数据集 (Rawlogs) 是 MRPT 的另一个目标，由多个类和应用程序支持。

  具体在这里是怎么用的看了代码才能知道，全部代码都包括在一个 cpp 中，可以！

add_executable(rf2o_laser_odometry_node src/CLaserOdometry2D.cpp)

---

int main(int argc, char** argv)
{
    ros::init(argc, argv, "RF2O_LaserOdom");
    CLaserOdometry2D myLaserOdom;
    ROS_INFO("initialization complete...Looping");
    ros::Rate loop_rate(myLaserOdom.freq);
    while (ros::ok()) {
        ros::spinOnce();        //Check for new laser scans
        if( myLaserOdom.is_initialized() && myLaserOdom.scan_available() ) {            
            //Process odometry estimation
            myLaserOdom.odometryCalculation();
        }
        else {
            ROS_WARN("Waiting for laser_scans....") ;
        }
        loop_rate.sleep();
    }
    return(0);
}

---

2.main 函数

首先就是新建了一个 激光里程计 对象，在该类的构造函数中，定义了激光数据的 topic 名称：/laser_scan，发布的 tf 坐标系关系 /base_link ，/odom ，以及发布的频率 freq ，都是一些基本的参数。然后就是定义了 接收 和 发送 topic。

在 main 函数的主循环中，需要判断是否进行了初始化 Init() 和 是否有新的激光数据，才会计算激光里程计。相当于两个线程在跑，一个通过消息回调接收数据，当有了新的数据，主循环中就会调用激光里程计计算位置信息。

3.回调函数与数据初始化

---

void CLaserOdometry2D::LaserCallBack(const sensor_msgs::LaserScan::ConstPtr& new_scan) {
    //Keep in memory the last received laser_scan
    last_scan = *new_scan;
    //Initialize module on first scan
    if (first_laser_scan) {
        Init();
        first_laser_scan = false;
    }
    else {   
        //copy laser scan to internal variable
        for (unsigned int i = 0; i<width; i++)
            range_wf(i) = new_scan->ranges[i];
        new_scan_available = true;
    }
}

在回调函数 LaserCallBack 中，也没做什么处理，会对一帧进行初始化 Init()，然后把后面的数据存到 range_wf 中，用于计算位置信息。

void CLaserOdometry2D::Init()
{
    // Got an initial scan laser, obtain its parametes 在第一帧激光数据，定义其参数
    ROS_INFO("Got first Laser Scan .... Configuring node");
    width = last_scan.ranges.size();    // Num of samples (size) of the scan laser 激光雷达的激光束数
    cols = width;						// Max reolution. Should be similar to the width parameter 
    fovh = fabs(last_scan.angle_max - last_scan.angle_min); // Horizontal Laser's FOV 激光雷达的水平视角
    ctf_levels = 5;                     // Coarse-to-Fine levels 设置一个由粗到细的 变换矩阵
    iter_irls = 5;                      //Num iterations to solve iterative reweighted least squares 最小二乘的迭代次数

    // Set laser pose on the robot (through tF) 通过 TF 设置激光雷达在小车上的位置
    // This allow estimation of the odometry with respect to the robot base reference system.
    // 得到的里程计信息是相对于机器人坐标系
    mrpt::poses::CPose3D LaserPoseOnTheRobot;
    tf::StampedTransform transform;
    try {
    	 // 得到激光坐标系 到 机器人坐标系的 转换关系
        tf_listener.lookupTransform("/base_link", last_scan.header.frame_id, ros::Time(0), transform);
    }
    catch (tf::TransformException &ex) {
        ROS_ERROR("%s",ex.what());
        ros::Duration(1.0).sleep();
    }

    //TF:transform -> mrpt::CPose3D (see mrpt-ros-bridge)
    const tf::Vector3 &t = transform.getOrigin(); // 平移
    LaserPoseOnTheRobot.x() = t[0];
    LaserPoseOnTheRobot.y() = t[1];
    LaserPoseOnTheRobot.z() = t[2];
    const tf::Matrix3x3 &basis = transform.getBasis(); // 旋转
    mrpt::math::CMatrixDouble33 R;
    for(int r = 0; r < 3; r++)
        for(int c = 0; c < 3; c++)
            R(r,c) = basis[r][c];
    LaserPoseOnTheRobot.setRotationMatrix(R);

    //Set the initial pose 设置激光雷达的初始位姿，在机器人坐标系下
    laser_pose = LaserPoseOnTheRobot;
    laser_oldpose = LaserPoseOnTheRobot;
    
    // Init module 初始化模型
    //-------------
    range_wf.setSize(1, width);

    //Resize vectors according to levels 初始化 由粗到精 的变化矩阵
    transformations.resize(ctf_levels);
    for (unsigned int i = 0; i < ctf_levels; i++)
        transformations[i].resize(3, 3);

    //Resize pyramid 调整金字塔大小
    unsigned int s, cols_i;
    const unsigned int pyr_levels = round(log2(round(float(width) / float(cols)))) + ctf_levels; // 金字塔层数，
    range.resize(pyr_levels);
    range_old.resize(pyr_levels);
    range_inter.resize(pyr_levels);
    xx.resize(pyr_levels);
    xx_inter.resize(pyr_levels);
    xx_old.resize(pyr_levels);
    yy.resize(pyr_levels);
    yy_inter.resize(pyr_levels);
    yy_old.resize(pyr_levels);
    range_warped.resize(pyr_levels);
    xx_warped.resize(pyr_levels);
    yy_warped.resize(pyr_levels);

    for (unsigned int i = 0; i < pyr_levels; i++) {
        s = pow(2.f, int(i));
        //每一层的尺度，1 - 0.5 - 0.25 - 0.125 - 0.0625
        cols_i = ceil(float(width) / float(s)); 
        
        range[i].resize(1, cols_i);
        range_inter[i].resize(1, cols_i);
        range_old[i].resize(1, cols_i);
        range[i].assign(0.0f);
        range_old[i].assign(0.0f);
        xx[i].resize(1, cols_i);
        xx_inter[i].resize(1, cols_i);
        xx_old[i].resize(1, cols_i);
        xx[i].assign(0.0f);
        xx_old[i].assign(0.0f);
        yy[i].resize(1, cols_i);
        yy_inter[i].resize(1, cols_i);
        yy_old[i].resize(1, cols_i);
        yy[i].assign(0.f);
        yy_old[i].assign(0.f);

        if (cols_i <= cols) {
            range_warped[i].resize(1, cols_i);
            xx_warped[i].resize(1, cols_i);
            yy_warped[i].resize(1, cols_i);
        }
    }

    dt.resize(1, cols);
    dtita.resize(1, cols);
    normx.resize(1, cols);
    normy.resize(1, cols);
    norm_ang.resize(1, cols);
    weights.setSize(1, cols);
    null.setSize(1, cols);
    null.assign(0);
    cov_odo.assign(0.f);

    fps = 1.f;		//In Hz
    num_valid_range = 0; // 有效的激光距离数据个数

    // Compute gaussian mask 计算高斯掩码  [1/16，1/4，6/16，1/4，1/16] 用于计算加权平均值
    g_mask[0] = 1.f / 16.f; g_mask[1] = 0.25f; g_mask[2] = 6.f / 16.f; g_mask[3] = g_mask[1]; g_mask[4] = g_mask[0];
	
    kai_abs.assign(0.f);
    kai_loc_old.assign(0.f);
 
    module_initialized = true; // 模型初始化完成
    last_odom_time = ros::Time::now();
}

总的来说，在初始化的过程中，载入了激光数据的参数信息，并且初始化了一些容器。现在参数、计算需要的容器以及激光数据如同待宰羔羊，那么下面就要开始上手干活了。

---

4.计算激光里程计的主循环

下面就是 main 函数中的 odometryCalculation，开始计算激光里程计，在原有的代码中，注释也很明确。

4.1 创建图像金字塔 createImagePyramid

首先是创建图像金字塔 createImagePyramid，

void CLaserOdometry2D::createImagePyramid() {
	const float max_range_dif = 0.3f; // 最大的距离差值
	//Push the frames back 更新数据
	range_old.swap(range);
	xx_old.swap(xx);
	yy_old.swap(yy);

  // 金字塔的层数与里程计计算中使用的层数不匹配（因为我们有时希望以较低的分辨率完成）
  unsigned int pyr_levels = round(log2(round(float(width)/float(cols)))) + ctf_levels;

  //Generate levels 开始创建金字塔
  for (unsigned int i = 0; i<pyr_levels; i++) {
    unsigned int s = pow(2.f,int(i)); // 每次缩放 2 倍
    cols_i = ceil(float(width)/float(s));
    const unsigned int i_1 = i-1; // 上一层

    //First level -> Filter (not downsampling); 
    if (i == 0) { // i = 0 第一层进行滤波
      for (unsigned int u = 0; u < cols_i; u++) {	
        const float dcenter = range_wf(u);	
        //Inner pixels  内部像素的处理， u从第三列开始到倒数第三列
        if ((u>1)&&(u<cols_i-2)) {		 
          if (dcenter > 0.f) {	// 当前激光距离大于0,一般都满足
            float sum = 0.f; // 累加量，用于计算加权平均值
            float weight = 0.f; // 权重
            for (int l=-2; l<3; l++) { // 取附近五个点
              const float abs_dif = abs(range_wf(u+l)-dcenter); // 该点附近的五个点的距离，与当前点距离的绝对误差
              if (abs_dif < max_range_dif) { // 误差满足阈值
                const float aux_w = g_mask[2+l]*(max_range_dif - abs_dif); // 认为越靠近该点的 权重应该最大，加权平均值
                weight += aux_w;
                sum += aux_w*range_wf(u+l);
              }
            }
          range[i](u) = sum/weight;
          }
          else // 否则当前激光距离设为0
            range[i](u) = 0.f;
        }
        
        //Boundary 下面对边界像素的处理
        else {
          if (dcenter > 0.f){	 // 判断激光距离是否合法			
            float sum = 0.f;
            float weight = 0.f;
            for (int l=-2; l<3; l++)	{ // 计算加权平均值，只不过需要判断是否会越界
              const int indu = u+l;
              if ((indu>=0)&&(indu<cols_i)){
                const float abs_dif = abs(range_wf(indu)-dcenter);										
                if (abs_dif < max_range_dif){
                  const float aux_w = g_mask[2+l]*(max_range_dif - abs_dif);
                  weight += aux_w;
                  sum += aux_w*range_wf(indu);
                }
              }
            }
            range[i](u) = sum/weight;
          }
          else
            range[i](u) = 0.f;
        }
      }
    }
    //-----------------------------------------------------------------------------
    // 从第二层开始，做下采样，同样也是分为内部点，和边界点进行处理，原理与第一层相同，计算加权平均值
    // 不过值得注意的是，从第二层开始 使用的数据是上一层下采样后的数据，即range[i_1]，因此每次计算都会缩小2倍。
    else {            
      for (unsigned int u = 0; u < cols_i; u++) {
        const int u2 = 2*u;		// 比上次缩小二倍
        const float dcenter = range[i_1](u2);
        //Inner pixels
        if ((u>0)&&(u<cols_i-1)){		
					if (dcenter > 0.f){	
					  float sum = 0.f;
						float weight = 0.f;
						for (int l=-2; l<3; l++){
							const float abs_dif = abs(range[i_1](u2+l)-dcenter);
							if (abs_dif < max_range_dif){
								const float aux_w = g_mask[2+l]*(max_range_dif - abs_dif);
								weight += aux_w;
								sum += aux_w*range[i_1](u2+l);
							}
						}
						range[i](u) = sum/weight;
					}
					else
						range[i](u) = 0.f;
        }
        //Boundary
        else{
          if (dcenter > 0.f){						
            float sum = 0.f;
            float weight = 0.f;
            const unsigned int cols_i2 = range[i_1].cols();
            for (int l=-2; l<3; l++)	{
              const int indu = u2+l;
              if ((indu>=0)&&(indu<cols_i2)) {
                const float abs_dif = abs(range[i_1](indu)-dcenter);										
                if (abs_dif < max_range_dif){
                  const float aux_w = g_mask[2+l]*(max_range_dif - abs_dif);
                  weight += aux_w;
                  sum += aux_w*range[i_1](indu);
                }
              }
            }
            range[i](u) = sum/weight;
          }
          else
            range[i](u) = 0.f;
        }
      }
    }

    //Calculate coordinates "xy" of the points 计算激光点的坐标
    for (unsigned int u = 0; u < cols_i; u++) {
      if (range[i](u) > 0.f){
        //以激光雷达的水平中间视角为0度，计算每束激光的角度
        const float tita = -0.5*fovh + float(u)*fovh/float(cols_i-1);
        xx[i](u) = range[i](u)*cos(tita);
        yy[i](u) = range[i](u)*sin(tita);
      }
      else {
        xx[i](u) = 0.f;
        yy[i](u) = 0.f;
      }
    }
  }
}

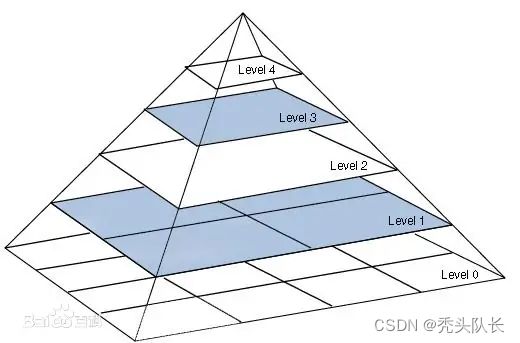
以上呢，就计算得到了每一层金字塔内所包含的点云位置，借用百度百科中的一张图，可以直观的看出图像金字塔的效果。不过这里是一个2D的金字塔，相当与降低了分辨率，用附近的点云距离，通过加权平均值算出一个”代表”。

---

4.2 金字塔处理的八个步骤

然后对于每一层金字塔的处理分为八个步骤，也是核心部分，首先对整个流程介绍一下，后面会对各个函数进行详细的介绍。

void CLaserOdometry2D::odometryCalculation()
{
    m_clock.Tic();
    createImagePyramid();  // 计算金字塔
    
    //Coarse-to-fine scheme // 从金字塔的顶端开始开始
    for (unsigned int i=0; i<ctf_levels; i++) {
        //Previous computations  首先把旋转矩阵初始化
        transformations[i].setIdentity();

        level = i; // 记录目前计算进度，因为上一层的计算会当作下一层的初值，由粗到细的迭代
        unsigned int s = pow(2.f,int(ctf_levels-(i+1)));  // 从金字塔的最顶端开始，所以需要做一下处理，计算出最高层的缩放系数
        cols_i = ceil(float(cols)/float(s));  // 缩放后的数据长度
        image_level = ctf_levels - i + round(log2(round(float(width)/float(cols)))) - 1; // 当前需要处理的金字塔层数

        //1. Perform warping 需要对金字塔数据进行裁剪，第一层就直接赋值
        if (i == 0) {
            range_warped[image_level] = range[image_level];
            xx_warped[image_level] = xx[image_level];
            yy_warped[image_level] = yy[image_level];
        }
        else
            performWarping(); // 其他层都是被缩放过的，所以数据的长度也会边短

        //2. Calculate inter coords  计算坐标
        calculateCoord();

        //3. Find null points 找到一些距离为0的点，因为在之前金字塔缩放的时候，距离小与0的不合法激光数据都被置为0了
        findNullPoints();

        //4. Compute derivatives 求导
        calculaterangeDerivativesSurface();

        //5. Compute normals 计算法线
        //computeNormals();

        //6. Compute weights 计算权重
        computeWeights();

        //7. Solve odometry 求解里程计
        if (num_valid_range > 3) {
            solveSystemNonLinear();
            //solveSystemOneLevel();    //without robust-function
        }

        //8. Filter solution 相当与是在恢复尺度，之前缩放后求出的位姿变化，要再恢复到缩放之前的位姿
        filterLevelSolution(); 
    }

    m_runtime = 1000*m_clock.Tac();
    ROS_INFO("Time odometry (ms): %f", m_runtime);

    //Update poses
    PoseUpdate();
    new_scan_available = false;     //avoids the possibility to run twice on the same laser scan
}

---

4.2.1 计算坐标

我们按照处理的顺序来，最高层并不会进行数据裁剪坐标转换这部分，因此直接计算坐标。

void CLaserOdometry2D::calculateCoord()
{		
	for (unsigned int u = 0; u < cols_i; u++) // 遍历该层的所有数据信息
	{
	  // 如果上一帧该层的数据 或者这一帧数据 为0就不处理
		if ((range_old[image_level](u) == 0.f) || (range_warped[image_level](u) == 0.f))
		{
			range_inter[image_level](u) = 0.f;
			xx_inter[image_level](u) = 0.f;
			yy_inter[image_level](u) = 0.f;
		}
		else // 否则 取两者均值
		{
			range_inter[image_level](u) = 0.5f*(range_old[image_level](u) + range_warped[image_level](u));
			xx_inter[image_level](u) = 0.5f*(xx_old[image_level](u) + xx_warped[image_level](u));
			yy_inter[image_level](u) = 0.5f*(yy_old[image_level](u) + yy_warped[image_level](u));
		}
	}
}

---

4.2.2 找到数据为0的点

void CLaserOdometry2D::findNullPoints()
{
	//Size of null matrix is set to its maximum size (constructor)
	// 记录空值的矩阵是 最大的数据大小，也就是和最底层的金字塔一样，不会访问越界
	num_valid_range = 0;
	for (unsigned int u = 1; u < cols_i-1; u++)
	{
		if (range_inter[image_level](u) == 0.f)
			null(u) = 1;
		else
		{
			num_valid_range++; // 记录有效激光点的个数
			null(u) = 0;
		}
	}
}

---

4.2.3 计算导数

void CLaserOdometry2D::calculaterangeDerivativesSurface()
{	
	//The gradient size ir reserved at the maximum size (at the constructor)
  //Compute connectivity
	rtita.resize(1,cols_i); 		//Defined in a different way now, without inversion
  rtita.assign(1.f); 

	// 计算相邻两点的 距离差值
	for (unsigned int u = 0; u < cols_i-1; u++)
  {
		const float dist = square(xx_inter[image_level](u+1) - xx_inter[image_level](u))
							+ square(yy_inter[image_level](u+1) - yy_inter[image_level](u));
		if (dist  > 0.f)
			rtita(u) = sqrt(dist);
	}

  //Spatial derivatives 空间导数，d = (r1 *(range3-range2) + r2 * (range2-range1))/(r1+r2)
  for (unsigned int u = 1; u < cols_i-1; u++)
  dtita(u) = (rtita(u-1)*(range_inter[image_level](u+1)-range_inter[image_level](u)) + rtita(u)*    
      (range_inter[image_level](u) - range_inter[image_level](u-1)))/(rtita(u)+rtita(u-1));
  // 第一对点 和 最后一对点 单独赋值
  dtita(0) = dtita(1);
	dtita(cols_i-1) = dtita(cols_i-2);

	//Temporal derivative 对时间求导得到速度
	for (unsigned int u = 0; u < cols_i; u++)
		dt(u) = fps*(range_warped[image_level](u) - range_old[image_level](u));
}

---

4.2.4 计算法线（未用到）

void CLaserOdometry2D::computeNormals()
{
	normx.assign(0.f);
	normy.assign(0.f);
	norm_ang.assign(0.f);

	const float incr_tita = fovh/float(cols_i-1);  
	for (unsigned int u=0; u<cols_i; u++)
	{
		if (null(u) == 0.f)
		{
			const float tita = -0.5f*fovh + float(u)*incr_tita; 
			const float alfa = -atan2(2.f*dtita(u), 2.f*range[image_level](u)*incr_tita);
			norm_ang(u) = tita + alfa;
			if (norm_ang(u) < -M_PI)
				norm_ang(u) += 2.f*M_PI;
			else if (norm_ang(u) < 0.f)
				norm_ang(u) += M_PI;
			else if (norm_ang(u) > M_PI)
				norm_ang(u) -= M_PI;

			normx(u) = cos(tita + alfa);
			normy(u) = sin(tita + alfa);
		}
	}
}

---

4.2.5 计算权重

void CLaserOdometry2D::computeWeights()
{
	//The maximum weight size is reserved at the constructor
	weights.assign(0.f);
	
	//Parameters for error_linearization
	const float kdtita = 1.f;
	const float kdt = kdtita/square(fps);
	const float k2d = 0.2f;
	
	for (unsigned int u = 1; u < cols_i-1; u++)
		if (null(u) == 0)
		{	
			// 计算导数
			const float ini_dtita = range_old[image_level](u+1) - range_old[image_level](u-1);  // 与上一帧的该处数据的距离差
			const float final_dtita = range_warped[image_level](u+1) - range_warped[image_level](u-1);

			const float dtitat = ini_dtita - final_dtita;
			const float dtita2 = dtita(u+1) - dtita(u-1);

			const float w_der = kdt*square(dt(u)) + kdtita*square(dtita(u)) + k2d*(abs(dtitat) + abs(dtita2));

			weights(u) = sqrt(1.f/w_der);
		}

	const float inv_max = 1.f/weights.maximum();
	weights = inv_max*weights;
}

---

4.2.6 计算里程计

通过 Cauchy M-estimatorrobust-function 求解系统

void CLaserOdometry2D::solveSystemNonLinear()
{
    A.resize(num_valid_range,3); Aw.resize(num_valid_range,3);
    B.setSize(num_valid_range,1); Bw.setSize(num_valid_range,1);
    unsigned int cont = 0;
    const float kdtita = float(cols_i-1)/fovh;

    //Fill the matrix A and the vector B
    //The order of the variables will be (vx, vy, wz)

    for (unsigned int u = 1; u < cols_i-1; u++)
        if (null(u) == 0)
        {
            // Precomputed expressions
            const float tw = weights(u);
            const float tita = -0.5*fovh + u/kdtita;

            //Fill the matrix A
            A(cont, 0) = tw*(cos(tita) + dtita(u)*kdtita*sin(tita)/range_inter[image_level](u));
            A(cont, 1) = tw*(sin(tita) - dtita(u)*kdtita*cos(tita)/range_inter[image_level](u));
            A(cont, 2) = tw*(-yy[image_level](u)*cos(tita) + xx[image_level](u)*sin(tita) - dtita(u)*kdtita);
            B(cont,0) = tw*(-dt(u));

            cont++;
        }

    // Solve the linear system of equations using a minimum least squares method
    // 使用最小二乘法求解线性方程组
    MatrixXf AtA, AtB;
    AtA.multiply_AtA(A);
    AtB.multiply_AtB(A,B);
    Var = AtA.ldlt().solve(AtB);

    //Covariance matrix calculation 	Cov Order -> vx,vy,wz 协方差矩阵计算
    MatrixXf res(num_valid_range,1);
    res = A*Var - B;
    //cout << endl << "max res: " << res.maxCoeff();
    //cout << endl << "min res: " << res.minCoeff();

    Compute the energy
    //Compute the average dt
    float aver_dt = 0.f, aver_res = 0.f; unsigned int ind = 0;
    for (unsigned int u = 1; u < cols_i-1; u++)
        if (null(u) == 0)
        {
            aver_dt += fabsf(dt(u));
            aver_res += fabsf(res(ind++));
        }
    aver_dt /= cont; aver_res /= cont;

    const float k = 10.f/aver_dt; //200
    //Solve iterative reweighted least squares 求解迭代加权最小二乘法
    for (unsigned int i=1; i<=iter_irls; i++)
    {
        cont = 0;

        for (unsigned int u = 1; u < cols_i-1; u++)
            if (null(u) == 0)
            {
                const float res_weight = sqrt(1.f/(1.f + square(k*res(cont))));

                //Fill the matrix Aw
                Aw(cont,0) = res_weight*A(cont,0);
                Aw(cont,1) = res_weight*A(cont,1);
                Aw(cont,2) = res_weight*A(cont,2);
                Bw(cont) = res_weight*B(cont);
                cont++;
            }

        //Solve the linear system of equations using a minimum least squares method 
        //使用最小二乘法求解线性方程组
        AtA.multiply_AtA(Aw);
        AtB.multiply_AtB(Aw,Bw);
        Var = AtA.ldlt().solve(AtB);
        res = A*Var - B;

    }

    cov_odo = (1.f/float(num_valid_range-3))*AtA.inverse()*res.squaredNorm();
    kai_loc_level = Var;
    std::cout << endl << "COV_ODO: " << cov_odo  << endl;
}

---

4.2.7 计算对应金字塔层的位姿

void CLaserOdometry2D::filterLevelSolution()
{
	//	计算特征值和特征向量
	SelfAdjointEigenSolver<MatrixXf> eigensolver(cov_odo);
	if (eigensolver.info() != Success) 
	{ 
		printf("Eigensolver couldn't find a solution. Pose is not updated");
		return;
	}
	
	//First, we have to describe both the new linear and angular speeds in the "eigenvector" basis
	//首先，我们必须在“特征向量”基础中描述新的线速度和角速度
	Matrix<float,3,3> Bii;
	Matrix<float,3,1> kai_b;
	Bii = eigensolver.eigenvectors();

	kai_b = Bii.colPivHouseholderQr().solve(kai_loc_level);

	//Second, we have to describe both the old linear and angular speeds in the "eigenvector" basis too
	//其次，我们也必须在“特征向量”基础中描述旧的线速度和角速度
	CMatrixFloat31 kai_loc_sub;

	//Important: we have to substract the solutions from previous levels
	//重要提示：我们必须从以前的层数中减去这个结果
	Matrix3f acu_trans;
	acu_trans.setIdentity();
	for (unsigned int i=0; i<level; i++)
		acu_trans = transformations[i]*acu_trans;

	kai_loc_sub(0) = -fps*acu_trans(0,2);
	kai_loc_sub(1) = -fps*acu_trans(1,2);
	if (acu_trans(0,0) > 1.f)
		kai_loc_sub(2) = 0.f;
	else
		kai_loc_sub(2) = -fps*acos(acu_trans(0,0))*sign(acu_trans(1,0));
	kai_loc_sub += kai_loc_old;

	Matrix<float,3,1> kai_b_old;
	kai_b_old = Bii.colPivHouseholderQr().solve(kai_loc_sub);

	//Filter speed
	const float cf = 15e3f*expf(-int(level)), df = 0.05f*expf(-int(level));

	Matrix<float,3,1> kai_b_fil;
	for (unsigned int i=0; i<3; i++)
	{
			kai_b_fil(i,0) = (kai_b(i,0) + (cf*eigensolver.eigenvalues()(i,0) + df)*kai_b_old(i,0))/(1.f + 
			    cf*eigensolver.eigenvalues()(i,0) + df);
			//kai_b_fil_f(i,0) = (1.f*kai_b(i,0) + 0.f*kai_b_old_f(i,0))/(1.0f + 0.f);
	}

	//Transform filtered speed to local reference frame and compute transformation
	//将滤波后的速度转换为局部参考系并计算转换
	Matrix<float,3,1> kai_loc_fil = Bii.inverse().colPivHouseholderQr().solve(kai_b_fil);

	//transformation
	const float incrx = kai_loc_fil(0)/fps;
	const float incry = kai_loc_fil(1)/fps;
	const float rot = kai_loc_fil(2)/fps;
	transformations[level](0,0) = cos(rot);
	transformations[level](0,1) = -sin(rot);
	transformations[level](1,0) = sin(rot);
	transformations[level](1,1) = cos(rot);
	transformations[level](0,2) = incrx;
	transformations[level](1,2) = incry;
}

---

4.2.8 金字塔缩放后的数据裁剪

void CLaserOdometry2D::performWarping()
{
	Matrix3f acu_trans;  // 3×3 的旋转矩阵
	acu_trans.setIdentity();  // 初始化单位阵
  // transformations 记录了从最上层到最下层，每一层计算的 位姿变化 结果，因此下一层需要拿上一层的结果当作初值
	for (unsigned int i=1; i<=level; i++)
		acu_trans = transformations[i-1]*acu_trans;

	MatrixXf wacu(1,cols_i); // 缩放后的激光数据大小
	wacu.assign(0.f);	
	range_warped[image_level].assign(0.f); // 由上往下

	const float cols_lim = float(cols_i-1); // 规定像素的边界
	const float kdtita = cols_lim/fovh; // 该层的像素边界 / 水平的视场角 = 该层的激光分辨率

	for (unsigned int j = 0; j<cols_i; j++) // 遍历该层的 所有激光数据
	{				
		if (range[image_level](j) > 0.f) // 距离不合法的不处理
		{
			//Transform point to the warped reference frame 
			const float x_w = acu_trans(0,0)*xx[image_level](j) + acu_trans(0,1)*yy[image_level](j) + acu_trans(0,2);
			const float y_w = acu_trans(1,0)*xx[image_level](j) + acu_trans(1,1)*yy[image_level](j) + acu_trans(1,2);
			const float tita_w = atan2(y_w, x_w);
			const float range_w = sqrt(x_w*x_w + y_w*y_w);

			//Calculate warping
			const float uwarp = kdtita*(tita_w + 0.5*fovh);

			//The warped pixel (which is not integer in general) contributes to all the surrounding ones
			if (( uwarp >= 0.f)&&( uwarp < cols_lim))
			{
				const int uwarp_l = uwarp;
				const int uwarp_r = uwarp_l + 1;
				const float delta_r = float(uwarp_r) - uwarp;
				const float delta_l = uwarp - float(uwarp_l);

				//Very close pixel
				if (abs(round(uwarp) - uwarp) < 0.05f)
				{
					range_warped[image_level](round(uwarp)) += range_w;
					wacu(round(uwarp)) += 1.f;
				}
				else
				{
					const float w_r = square(delta_l);
					range_warped[image_level](uwarp_r) += w_r*range_w;
					wacu(uwarp_r) += w_r;

					const float w_l = square(delta_r);
					range_warped[image_level](uwarp_l) += w_l*range_w;
					wacu(uwarp_l) += w_l;
				}
			}
		}
	}

	//Scale the averaged range and compute coordinates 缩放平均距离并计算坐标
	for (unsigned int u = 0; u<cols_i; u++)
	{	
		if (wacu(u) > 0.f)
		{
			const float tita = -0.5f*fovh + float(u)/kdtita;
			range_warped[image_level](u) /= wacu(u);
			xx_warped[image_level](u) = range_warped[image_level](u)*cos(tita);
			yy_warped[image_level](u) = range_warped[image_level](u)*sin(tita);
		}
		else
		{
			range_warped[image_level](u) = 0.f;
			xx_warped[image_level](u) = 0.f;
			yy_warped[image_level](u) = 0.f;
		}
	}
}

---

4.3 位姿更新

void CLaserOdometry2D::PoseUpdate()
{
	//First, compute the overall transformation
	//---------------------------------------------------
	Matrix3f acu_trans;
	acu_trans.setIdentity();
	for (unsigned int i=1; i<=ctf_levels; i++)
		acu_trans = transformations[i-1]*acu_trans;


	//				Compute kai_loc and kai_abs
	//--------------------------------------------------------
	kai_loc(0) = fps*acu_trans(0,2);
	kai_loc(1) = fps*acu_trans(1,2);
	if (acu_trans(0,0) > 1.f)
		kai_loc(2) = 0.f;
	else
		kai_loc(2) = fps*acos(acu_trans(0,0))*sign(acu_trans(1,0));

	//cout << endl << "Arc cos (incr tita): " << kai_loc(2);

	float phi = laser_pose.yaw();

	kai_abs(0) = kai_loc(0)*cos(phi) - kai_loc(1)*sin(phi);
	kai_abs(1) = kai_loc(0)*sin(phi) + kai_loc(1)*cos(phi);
	kai_abs(2) = kai_loc(2);


	//						Update poses
	//-------------------------------------------------------
	laser_oldpose = laser_pose;
	math::CMatrixDouble33 aux_acu = acu_trans;
	poses::CPose2D pose_aux_2D(acu_trans(0,2), acu_trans(1,2), kai_loc(2)/fps);
    laser_pose = laser_pose + pose_aux_2D;



	//				Compute kai_loc_old
	//-------------------------------------------------------
	phi = laser_pose.yaw();
	kai_loc_old(0) = kai_abs(0)*cos(phi) + kai_abs(1)*sin(phi);
	kai_loc_old(1) = -kai_abs(0)*sin(phi) + kai_abs(1)*cos(phi);
	kai_loc_old(2) = kai_abs(2);


    ROS_INFO("LASERodom = [%f %f %f]",laser_pose.x(),laser_pose.y(),laser_pose.yaw());


    // GET ROBOT POSE from LASER POSE
    //------------------------------  
    mrpt::poses::CPose3D LaserPoseOnTheRobot_inv;
    tf::StampedTransform transform;
    try
    {
        tf_listener.lookupTransform(last_scan.header.frame_id, "/base_link", ros::Time(0), transform);
    }
    catch (tf::TransformException &ex)
    {
        ROS_ERROR("%s",ex.what());
        ros::Duration(1.0).sleep();
    }

    //TF:transform -> mrpt::CPose3D (see mrpt-ros-bridge)
    const tf::Vector3 &t = transform.getOrigin();
    LaserPoseOnTheRobot_inv.x() = t[0];
    LaserPoseOnTheRobot_inv.y() = t[1];
    LaserPoseOnTheRobot_inv.z() = t[2];
    const tf::Matrix3x3 &basis = transform.getBasis();
    mrpt::math::CMatrixDouble33 R;
    for(int r = 0; r < 3; r++)
        for(int c = 0; c < 3; c++)
            R(r,c) = basis[r][c];
    LaserPoseOnTheRobot_inv.setRotationMatrix(R);

    //Compose Transformations
    robot_pose = laser_pose + LaserPoseOnTheRobot_inv;
    ROS_INFO("BASEodom = [%f %f %f]",robot_pose.x(),robot_pose.y(),robot_pose.yaw());


    // Estimate linear/angular speeds (mandatory for base_local_planner)
    // last_scan -> the last scan received
    // last_odom_time -> The time of the previous scan lasser used to estimate the pose
    //-------------------------------------------------------------------------------------
    double time_inc_sec = (last_scan.header.stamp - last_odom_time).toSec();
    last_odom_time = last_scan.header.stamp;
    double lin_speed = acu_trans(0,2) / time_inc_sec;
    //double lin_speed = sqrt( square(robot_oldpose.x()-robot_pose.x()) + square(robot_oldpose.y()-robot_pose.y()) )/time_inc_sec;
    double ang_inc = robot_pose.yaw() - robot_oldpose.yaw();
    if (ang_inc > 3.14159)
        ang_inc -= 2*3.14159;
    if (ang_inc < -3.14159)
        ang_inc += 2*3.14159;
    double ang_speed = ang_inc/time_inc_sec;
    robot_oldpose = robot_pose;
}

后面会详细推导公式，未完待更…