强化学习笔记（七）演员-评论家算法（Actor-Critic Algorithms）及Pytorch实现

接着上一节的学习笔记。上一节学习总结了Policy Gradient方法以及蒙特卡洛Reinforce实现。这节了解一下Actor-Critic算法。Actor-Critic是2000年在NIPS上发表的一篇名为 Actor-Critic Algorithms的论文中提出的。它是一种策略(Policy Based)和价值(Value Based)相结合的方法，见UCL第七讲的开篇PPT（下图）

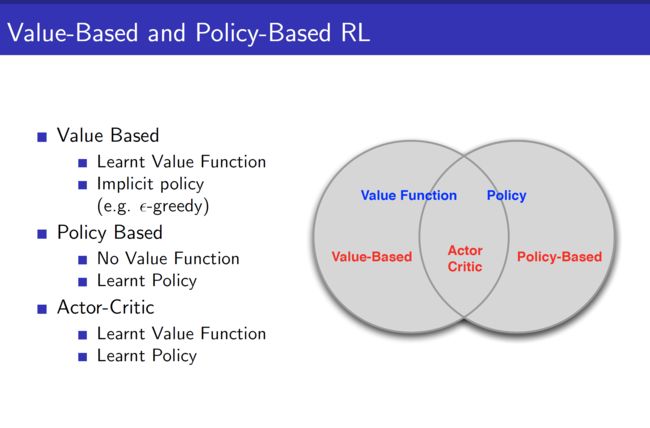
Q1: Actor-Critic的含义，与纯策略梯度法的不同？

第一个是Actor角色，在一些资料中也称为“演员角色”。这个角色是一个相对独立的模型，你仍然可以把它理解成一个神经网络，任务就是学动作。优化它的过程和优化一个普通DQN里面的网络没有太大的区别。
另一个是Critic角色，或者称作“评论家角色”。它负责评估Actor的表现，并指导Actor下一阶段的动作。这个角色也是一个独立的模型。在这种思维的指导下，估值学习也是一个独立的、可优化的任务，需要通过一个模型进行拟合。动作输出也是一个模型，通过一个模型进行拟合。
这种思想有点类似GAN网络中的生成器和判别器，两者相互监督和牵制，最后达到较好的效果。如果之前的DQN，Policy Gradient梯度上升公式及蒙特卡洛Reinforce算法都看懂了的话，这里还是很好理解的。
与Monte Carlo Policy Gradient不同，Actor Critic放弃利用回报来评估真实价值函数，而直接使用Critic算法，利用函数逼近法(Function Approximation Methods)即神经网络，利用逼近策略梯度法而非真实策略梯度。

Q2: 基线(Baseline)和优势函数(Advantage Function)的理解

策略梯度的更新公式如下：
$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)Q_w(s,a)\right]$$
上一节已经讲过，${\nabla }_{\theta }\log {\pi }_{\theta }(s,a)$是分值函数(Score Function)，它是固定不动的，因为我们要更新的变量就是策略${\pi }_{\theta }(s,a)$. 对$Q_w(s,a)$，能不能做做文章呢？通过理论推导，可以发现引入一个Baseline函数$B(s)$，只要它不随动作a变化，上述等式依然成立，这是因为减的那一项是0.
$$\begin{array}{rl}{\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)B(s)\right]& =\sum _{s\in \mathcal{S}}{d}^{{\pi }_{\theta }}(s)\sum _a{\nabla }_{\theta }{\pi }_{\theta }(s,a)B(s)\\ & =\sum _{s\in \mathcal{S}}{d}^{{\pi }_{\theta }}B(s){\nabla }_{\theta }\sum _{a\in \mathcal{A}}{\pi }_{\theta }(s,a)\\ & =\sum _{s\in \mathcal{S}}{d}^{{\pi }_{\theta }}B(s)\nabla 1\\ & =0\end{array}$$
令$B(s)=V^{\pi }\theta (s)$，引入优势函数(Advantage Function)——$A^{{\pi }_{\theta }}(s,a)$.
$$\begin{array}{rl}{A}^{{\pi }_{\theta }}(s,a)& =Q^{{\pi }_{\theta }}(s,a)-V^{{\pi }_{\theta }}(s)\\ {\nabla }_{\theta }J(\theta )& ={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)A^{{\pi }_{\theta }}(s,a)\right]\end{array}$$
两者的期望一样，优势函数有什么意义？从上节Monte Carlo 策略梯度法可以看到，更新项是蒙特卡洛采样的target return，这样导致的方差会很大。而使用优势函数可以显著地减少策略梯度的方差。
Critic（评论家）的任务就是要评估优势函数，而TD error的期望刚好就是优势函数：

基于Pytorch的Actor-Critic实现

参考Tensorflow版本：https://github.com/ljpzzz/machinelearning/blob/master/reinforcement-learning/actor_critic.py

代码改了很久，在一些很简单的地方被卡住了。主要注意的是td_error是Critic的Q网络算出来的值，直接返回是带第一个网络梯度的，这时候需要去掉这个梯度，不然在Actor更新的时候就会报错。
另外，这个代码很难收敛，我一直持续在9分上不去了。不过写一遍确实有助于对策略-价值双网络的理解。

程序流程

1. 实例化actor / critic 并初始化超参数
2. for Epochs:
     for Steps:
         ① 用actor选动作
         ② Step(state, action) 状态转移
         ③ 用critic的Q_Net算V(s)和V(s’)
            得TD_error = r + γV(s’)-V(s)
             顺便用TD_error的均方误差训练Q_Network
         ④ TD_error反馈给Actor，Policy Gradient公式 训练Actor
         ⑤ state = next_state

"""
@ Author: Peter Xiao
@ Date: 2020/7/23
@ Filename: Actor_critic.py
@ Brief: 使用 Actor-Critic算法训练CartPole-v0
"""

import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import time

# Hyper Parameters for Actor
GAMMA = 0.95  # discount factor
LR = 0.01  # learning rate

# Use GPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
torch.backends.cudnn.enabled = False  # 非确定性算法


class PGNetwork(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(PGNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, 20)
        self.fc2 = nn.Linear(20, action_dim)

    def forward(self, x):
        out = F.relu(self.fc1(x))
        out = self.fc2(out)
        return out

    def initialize_weights(self):
        for m in self.modules():
            nn.init.normal_(m.weight.data, 0, 0.1)
            nn.init.constant_(m.bias.data, 0.01)


class Actor(object):
    # dqn Agent
    def __init__(self, env):  # 初始化
        # 状态空间和动作空间的维度
        self.state_dim = env.observation_space.shape[0]
        self.action_dim = env.action_space.n

        # init network parameters
        self.network = PGNetwork(state_dim=self.state_dim, action_dim=self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.network.parameters(), lr=LR)

        # init some parameters
        self.time_step = 0

    def choose_action(self, observation):
        observation = torch.FloatTensor(observation).to(device)
        network_output = self.network.forward(observation)
        with torch.no_grad():
            prob_weights = F.softmax(network_output, dim=0).cuda().data.cpu().numpy()
        # prob_weights = F.softmax(network_output, dim=0).detach().numpy()
        action = np.random.choice(range(prob_weights.shape[0]),
                                  p=prob_weights)  # select action w.r.t the actions prob
        return action

    def learn(self, state, action, td_error):
        self.time_step += 1
        # Step 1: 前向传播
        softmax_input = self.network.forward(torch.FloatTensor(state).to(device)).unsqueeze(0)
        action = torch.LongTensor([action]).to(device)
        neg_log_prob = F.cross_entropy(input=softmax_input, target=action, reduction='none')

        # Step 2: 反向传播
        # 这里需要最大化当前策略的价值，因此需要最大化neg_log_prob * tf_error,即最小化-neg_log_prob * td_error
        loss_a = -neg_log_prob * td_error
        self.optimizer.zero_grad()
        loss_a.backward()
        self.optimizer.step()


# Hyper Parameters for Critic
EPSILON = 0.01  # final value of epsilon
REPLAY_SIZE = 10000  # experience replay buffer size
BATCH_SIZE = 32  # size of minibatch
REPLACE_TARGET_FREQ = 10  # frequency to update target Q network


class QNetwork(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(QNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, 20)
        self.fc2 = nn.Linear(20, 1)   # 这个地方和之前略有区别，输出不是动作维度，而是一维

    def forward(self, x):
        out = F.relu(self.fc1(x))
        out = self.fc2(out)
        return out

    def initialize_weights(self):
        for m in self.modules():
            nn.init.normal_(m.weight.data, 0, 0.1)
            nn.init.constant_(m.bias.data, 0.01)


class Critic(object):
    def __init__(self, env):
        # 状态空间和动作空间的维度
        self.state_dim = env.observation_space.shape[0]
        self.action_dim = env.action_space.n

        # init network parameters
        self.network = QNetwork(state_dim=self.state_dim, action_dim=self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.network.parameters(), lr=LR)
        self.loss_func = nn.MSELoss()

        # init some parameters
        self.time_step = 0
        self.epsilon = EPSILON  # epsilon值是随机不断变小的

    def train_Q_network(self, state, reward, next_state):
        s, s_ = torch.FloatTensor(state).to(device), torch.FloatTensor(next_state).to(device)
        # 前向传播
        v = self.network.forward(s)     # v(s)
        v_ = self.network.forward(s_)   # v(s')

        # 反向传播
        loss_q = self.loss_func(reward + GAMMA * v_, v)
        self.optimizer.zero_grad()
        loss_q.backward()
        self.optimizer.step()

        with torch.no_grad():
            td_error = reward + GAMMA * v_ - v

        return td_error


# Hyper Parameters
ENV_NAME = 'CartPole-v0'
EPISODE = 3000  # Episode limitation
STEP = 3000  # Step limitation in an episode
TEST = 10  # The number of experiment test every 100 episode


def main():
    # initialize OpenAI Gym env and dqn agent
    env = gym.make(ENV_NAME)
    actor = Actor(env)
    critic = Critic(env)

    for episode in range(EPISODE):
        # initialize task
        state = env.reset()
        # Train
        for step in range(STEP):
            action = actor.choose_action(state)  # SoftMax概率选择action
            next_state, reward, done, _ = env.step(action)
            td_error = critic.train_Q_network(state, reward, next_state)  # gradient = grad[r + gamma * V(s_) - V(s)]
            actor.learn(state, action, td_error)  # true_gradient = grad[logPi(s,a) * td_error]
            state = next_state
            if done:
                break

        # Test every 100 episodes
        if episode % 100 == 0:
            total_reward = 0
            for i in range(TEST):
                state = env.reset()
                for j in range(STEP):
                    env.render()
                    action = actor.choose_action(state)  # direct action for test
                    state, reward, done, _ = env.step(action)
                    total_reward += reward
                    if done:
                        break
            ave_reward = total_reward/TEST
            print('episode: ', episode, 'Evaluation Average Reward:', ave_reward)


if __name__ == '__main__':
    time_start = time.time()
    main()
    time_end = time.time()
    print('Total time is ', time_end - time_start, 's')