【深度学习】吴恩达深度学习-Course1神经网络与深度学习-第四周深度神经网络的关键概念编程(上)——一步步建立深度神经网络
勘误:
- 2021年12月10日12:46:21:纠正了三、反向传播模块中线性反向传播的问题。db不应该断言其为一个实数,只要其保持与b.shape相同的维度就好了,也不需要对其进行降维,否则对后边实战会有影响。总代码也已经更新。
- 2022年1月30日09:25:43:初始化L层神经网络(第三大点的第1续爱短板的1.2有误。我写错了bi的初始化。没使用0来初始化。且在初始化W时候的方式使用了"He initialization"(初始化方式会在course2中学到):
parameters["W" + str(i)] = np.random.randn(layer_dims[i], layer_dims[i - 1]) / np.sqrt(layer_dims[i - 1]),这里暂时不需要理解这种初始化方式,在course2中理解即可,如果这里使用原来的初始化方式会导致梯度下降滞塞。
视频链接:[【中英字幕】吴恩达深度学习课程第一课 — 神经网络与深度学习](https://www.bilibili.com/video/BV164411m79z?p=1) 学习链接:
- 【中文】【吴恩达课后编程作业】Course 1 - 神经网络和深度学习 - 第四周作业(1&2)
- Building your Deep Neural Network: Step by Step
- Deep Neural Network for Image Classification: Application
- python中除号/和//的区别
目录
- 〇、作业目标
- 一、一些必要的包
- 二、任务大纲(理论准备)
- 三、学习步骤
-
- 1.初始化
-
- 1.1 两层神经网络
- 1.2 L层的神经网络
- 2.前向传播模块
-
- 2.1 线性前向传播
- 2.2 线性激活函数的正向传播
- 2.3 正向传播L层模型
- 3.成本函数
- 4.反向传播模块
-
- 4.1 线性反向传播
- 4.2 线性激活函数的反向传播
- 4.3 反向传播L层模型
- 5.更新参数
- 四、概括
- 五、总代码
〇、作业目标
在前面的作业中,我们已经训练了2层的神经网络(其中一层为隐藏层)。在这一篇内容中,我们将学习如何建立深度神经网络,该神经网络有着许多你想要的层!
- 在这一次作业中,我们将完成构建深度神经网络所必须的函数。
- 在本篇的(下)中,我们将使用这一篇(上)中所建立的深度神经网络进行图像分类。
在本次作业后,我们将学会:
- 使用非线性单元如ReLU来改进我们的模型
- 建立一个深层神经网络(有超过一层的隐藏层)
- 完成更多易于使用的神经网络类
一、一些必要的包
我们在pyCharm中(这里使用Anaconda进行环境配置,使用PyCharm进行编程)导入如下的包:
- numpy:科学计算包
- matplotlib:绘图的Python库
- dnn_utils、testCases由此处下载,提取码为:xx1w。若提取码不对,请参考学习链接1中的提取码,此处的链接出自他。
如果你不知道怎么安装,可以参考我前边的文章:
- 【深度学习】吴恩达深度学习-Course1神经网络与深度学习-第二周神经网络基础编程
- 【深度学习】吴恩达深度学习-Course1神经网络与深度学习-第三周浅层神经网络编程
这两篇文章中使用环境和库的安装可能会帮到你。
在main.py中输入一下下面这段代码看看所需的包是否都有了,如果有报红的,请卸载后重新安装或尝试其他的方法:
import numpy as np
import h5py
import matplotlib.pyplot as plt
from course1.week4.testCases import *
from course1.week4.dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
np.random.seed(1)
二、任务大纲(理论准备)
为了建立神经网络,你需要完善很多函数。这些函数将会被在下一个任务建立两层和L层神经网络时用到。每一个小的函数都会帮助你完善接下来的介绍的这些步骤,这里有一个任务大纲,你将:
- 初始化两层网络和L层神经网络
- 完成前向传播模块(下边图中的紫色部分)
1.完成一层的线性部分前向传播步骤(得到Z^ [l])
2.写出激活函数(ReLU/Sigmoid)
3.连接前面两个步骤得到一个新的【线性->激活】的前向传播函数
4.叠加【线性->ReLU】前向传播函数L-1次(对1至L-1层)并在第L层叠加一个【线性->Sigmoid】函数。这将帮助你形成一个新的L层模型的前向传播函数。 - 计算损失
- 完成反向传播模块(下边图中的红色部分)
1.完成线性部分的后向传播步骤
2.写出激活函数的导数(ReLU_backward/sigmoid_backward)
3.连接前面两个步骤得到一个新的【线性->激活】反向传播函数
4.叠加【线性->ReLU】的反向传播函数L-1次并叠加【线性->Sigmoid】函数在L_model_backward函数中 - 最后更新参数

三、学习步骤
1.初始化
1.1 两层神经网络
目标:创建并初始化一个两层的神经网络所需要的参数(初始化W1,b1,W2,b2)
引导步骤:
- 要求的模型是这样的:LINEAR -> RELU -> LINEAR -> SIGMOID
- 随机初始化权重矩阵。使用
np.random.randn(shape)*0.01来初始化 - 用“0”来初始化偏差:
np.zeros(shape)
可以尝试自己写一下函数initialize_parameters(n_x, n_h, n_y),其中:
- n_x:输入层大小
- n_h:隐藏层大小
- n_y:输出层大小
需要返回一个parameters字典,包含以下信息:
- W1,维度为(n_h,n_x)的权重矩阵
- b1,维度为(n_h,1)的偏差向量
- W2,维度为(n_y,n_h)的权重矩阵
- b2,维度为(n_y,1)的偏差向量
尝试自己动手写一下吧!
这个初始化的写法如下:
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(1)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
写好后直接复制下边的代码测试一下:(一块一块地测试,就可以知道自己哪一步写的不对)
parameters = initialize_parameters(2,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
结果为
W1 = [[ 0.01624345 -0.00611756]
[-0.00528172 -0.01072969]]
b1 = [[ 0.]
[ 0.]]
W2 = [[ 0.00865408 -0.02301539]]
b2 = [[ 0.]]
1.2 L层的神经网络
理论基础:
L层神经网络的初始化非常复杂因为有很多权重矩阵和偏差向量。当完成下边的initialize_parameters_deep函数时,你需要确定你的函数能够匹配任意层数的维度。回顾一下,n^ [l]是第l层的单元数,因此,例如我们输入的X的大小是(12288,209)(即m = 209个样本),则:

记住,当在Python中计算WX+b时,会触发广播机制,例如,如果有以下的W、X和b:

则WX+b将会为:
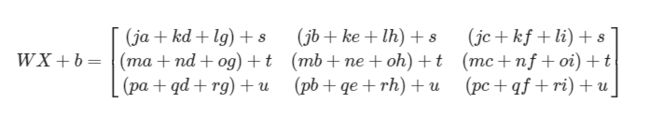
目标: 为L层神经网络进行初始化
引导步骤:
- 模型结构是这样的:【LINEAR -> RELU】 × (L-1) -> LINEAR -> SIGMOID。即前L-1层使用ReLU激活函数且最后一层使用Sigmoid激活函数。
- 随机初始化权重矩阵可以使用这个方法:
np.random.randn(shape) * 0.01 - 用0初始化偏差:
np.zeros(shape) - 我们将存储把不同层的单元数量存储在变量
layer_dims中。例如,在上一周我们练习平面数据集分类模型时,有2个输入,隐藏层有4个隐藏单元,输出层有1个输出单元,这意味着W1的维度是(4,2),b1的维度是(4,1),W2的维度是(1,4),b2的维度是(1,1)。你可以将此原理概括至L层中。 - 这里有一个L=1(一层神经网络)的补充。它将启发你完善L层神经网络的整体案例。
if L == 1:
parameters["W" + str(L)] = np.random.randn(layer_dims[1], layer_dims[0]) * 0.01
parameters["b" + str(L)] = np.zeros((layer_dims[1], 1))
这里我们要求指定随机种子:np.random.seed(3)
那么,尝试完善一下你的函数:initialize_parameters_deep(layer_dims)吧!其中:
- layer_dims为包含我们神经网络每一层维度的python的数组(列表)
这个函数需要返回:
- 一个包含参数“W1”,“b1”…,“WL”,"bL"的Python字典:Wl为维度是(layer_dims[l],layer_dims[l-1])的权重矩阵,bl是维度是(layer_dims[l],1)的偏差向量
def initialize_parameters_deep(layer_dims):
np.random.seed(3)
parameters = {}
L = len(layer_dims)
for i in range(1, L):
parameters["W" + str(i)] = np.random.randn(layer_dims[i], layer_dims[i - 1]) / np.sqrt(layer_dims[i - 1])
parameters["b" + str(i)] = np.zeros(shape=(layer_dims[i], 1))
assert (parameters["W" + str(i)].shape == (layer_dims[i], layer_dims[i - 1]))
assert (parameters["b" + str(i)].shape == (layer_dims[i], 1))
return parameters
直接复制下面这一段函数测试一下:
parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
结果应为:
W1 = [[ 0.01788628 0.0043651 0.00096497 -0.01863493 -0.00277388]
[-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218]
[-0.01313865 0.00884622 0.00881318 0.01709573 0.00050034]
[-0.00404677 -0.0054536 -0.01546477 0.00982367 -0.01101068]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[-0.01185047 -0.0020565 0.01486148 0.00236716]
[-0.01023785 -0.00712993 0.00625245 -0.00160513]
[-0.00768836 -0.00230031 0.00745056 0.01976111]]
b2 = [[0.]
[0.]
[0.]]
2.前向传播模块
现在你已经完成了参数的初始化,接下来,你将要做的是前向传播模块。你将从完善一些接下来你看到的基础函数开始一步步完善模型。在这个部分中你将要完成3个函数:
- LINEAR
- LINEAR -> ACTIVATION,这个激活函数会是ReLU或Sigmoid
- 整个模型是【LINEAR -> ReLU】× (L - 1)-> LINEAR ->Sigmoid
2.1 线性前向传播
线性化模块(将所有的例子向量化)通过以下的等式计算:
![]()
在这其中,
![]()
目标: 建立线性部分的前向传播
提示: 在计算上边的等式时,你会发现np.dot()很好用,如果你的维度不匹配,打印W.shape可能会对你有帮助。
那么,尝试完善一下你函数linear_forward(A, W, b)吧~
其中:
- A是前一层激活函数的结果(或者是输入的数据)
- W是权重矩阵
- b为偏差向量
要求你返回:
- Z:激活函数的输入,也叫做激活函数的参数
- cache:包含“A”,“W”,“b”的Python字典,存储下来用于高效计算反向传播部分
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
在这里说一下断言内的意思,为什么Z.shape == (W.shape[0], A.shape[1])?
首先要明白,shape[0]和shape[1]是什么意思。举个例子,有一个矩阵的shape是(4,3),那么这个矩阵的shape[0]就是4,shape[1]就是3,即4行3列。
在矩阵相乘中,我们要求前边这个参数的列数要等于后边这个参数的行数,而乘出来的结果就是(前边参数的行数,后边参数的列数)。这里np.dot(W, A)得到的结果就是(W.shape[0], A.shape[1]),而b的shape为(W.shape[0],1)(注意,b的行数是和W的行数保持一致的,从上边初始化的内容就能够理解)。在两个结果相加时,会触发广播机制,将b的一列复制为A.shape[1]列。从而得到Z的维度就是(W.shape[0], A.shape[1])。
直接复制下边的代码,测试一下你的函数:
A, W, b = linear_forward_test_case()
Z, linear_cache = linear_forward(A, W, b)
print("Z = " + str(Z))
结果是(这里我和原作者【学习链接2】出现了偏差(可能是种子有问题),我复制原作者的代码与此结果相同):
Z = [[ 3.26295337 -1.23429987]]
2.2 线性激活函数的正向传播
在这里,你将要使用两个激活函数。
- Sigmoid:
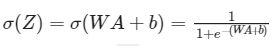
我们将给你提供Sigmoid函数。这个函数返回两个值:激活值“a”和包含“Z”的“cache”(这将在反向传播中被使用到)。要想使用它你只需要这么写:A, activation_cache = sigmoid(Z)。 - ReLU:ReLU的数学公式是这样的:
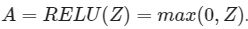
我们将给你提供ReLU函数。这个函数返回两个值:激活值“a”和包含“Z”的“cache”(这将在反向传播中被使用到)。要想使用它你只需要这么写:A, activation_cache = relu(Z)。
为了更方便,你需要组合两个函数(Linear和Activation)到一个函数中(Linear->Activation
)。在这里,你将完善一个函数,它会完成线性前向传播步骤,随后是激活传播步骤。
目标: 完成前向传播层,实现LINEAR -> ACTIVATION。数学关系在这里:
![]()
这里的激活函数“g”就是sigmoid()或relu()。使用前边我们写好的linear_forward()和正确的激活函数来完成linear_activation_forward(A_prev, W, b, activation)其中:
- A_prev:前一层的激活函数计算出的结果
- W:权重矩阵
- b:偏差向量
- activation:是一个字符串,可能是“relu”,也可能是“sigmoid”
返回:
- A:激活函数输出的结果
- cache:包括"linear_cache"和"activation_cache"的python字典,存储
def linear_activation_forward(A_prev, W, b, activation):
Z, linear_cache = linear_forward(A_prev, W, b)
if activation == "sigmoid":
A, activation_cache = sigmoid(Z)
elif activation == "relu":
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
经过激活,A的维度和Z的维度其实还是一样的。
直接复制下边的代码:测试一下你的函数是否正确:
A_prev, W, b = linear_activation_forward_test_case()
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
print("With sigmoid: A = " + str(A))
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
print("With ReLU: A = " + str(A))
结果为(这里我和原作者【学习链接2】出现了偏差(可能是种子有问题),我复制原作者的代码与此结果相同):
With sigmoid: A = [[0.96890023 0.11013289]]
With ReLU: A = [[3.43896131 0. ]]
2.3 正向传播L层模型
为了在完成L层神经网络时更便利,你需要一个函数来复制linear_activation_forward with ReLU L - 1次,然后再使用linear_activation_forward with SIGMOID.

目标: 完善上面模型中的前向传播
声明: 在接下来的代码中,AL代表
![]()
这有时候也称为Y帽。
提示:
- 使用你前边已经写好的函数
- 使用一个循环来重复【LINEAR -> ReLU】共(L-1)次。
- 不要忘记持续追踪caches并将它添加至caches列表。添加一个新变量c到列表中,你可以使用
list.append(c)
那么,请开始写你的函数:L_model_forward(X, parameters)吧!
其中:
- X:输入的数据
- parameters:initialize_parameters_deep()的输出
需要返回:
- AL:最后的激活值
- caches:caches的列表,包括如下内容:
每一个由linear_relu_forward()得到的缓存(一共有L-1个,索引从0到L-2)
由linear_sigmoid_forward()得到的缓存(只有一个,索引为L-1)
def L_model_forward(X, parameters):
caches = []
A = X
# 每一层都应该有W和B两个参数,所以parameters//2就是层数
L = len(parameters) // 2 # 这里的除号意思是“地板除”,除完后向下取整,见学习链接4
# 0-(L-1)层我们使用ReLU方法
for i in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev,
parameters["W" + str(i)],
parameters["b" + str(i)],
activation="relu")
caches.append(cache)
# 第L层(最后一层)我们使用sigmoid方法使最终结果处于0-1之间
AL, cache = linear_activation_forward(A,
parameters["W" + str(L)],
parameters["b" + str(L)],
activation="sigmoid")
caches.append(cache)
assert (AL.shape == (1, X.shape[1]))
return AL, caches
博主认为倒数第二行的断言写下边这句更准确。因为parameters[“W” + str(L)].shape[0]就是神经网络第L层的单元数
assert (AL.shape == (parameters["W" + str(L)].shape[0], X.shape[1]))
复制下边的代码测试一下你的函数吧!:
X, parameters = L_model_forward_test_case()
AL, caches = L_model_forward(X, parameters)
print("AL = " + str(AL))
print("Length of caches list = " + str(len(caches)))
这里中见到的“//”两个除号是地板除,详见:python中除号/和//的区别。即在完成除法操作后向下取整。
结果为(这里我和原作者【学习链接2】出现了偏差(可能是种子有问题),我复制原作者的代码与此结果相同):
AL = [[0.17007265 0.2524272 ]]
Length of caches list = 2
到现在为止,我们已经完成了完整的前向传播,输入X从而输出包含着预测结果的A^ [l],同时也记录了中间的缓存在“caches”中。使用这里的A^ [l],我们可以计算预测的损失。
3.成本函数
到这里,你已经完成了前向传播,你需要计算成本,因为你需要通过计算成本来检查你的模型是否真的在学习。
目标: 计算叉乘损失J,只需要使用下面的公式:
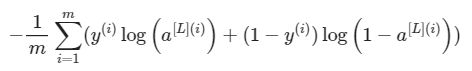
接下来,请利用你已有的知识完成成本函数的计算吧!compute_cost(AL, Y)
其中,AL是预测的值,Y是真实的“标签”,需要你输出损失函数的值。
def compute_cost(AL, Y):
# m,即数据集的大小,Y的大小是(1,m)
m = Y.shape[1]
# 根据公式写出损失函数
cost = -(1 / m) * (np.sum(np.multiply(Y, np.log(AL)) + np.multiply(1 - Y, np.log(1 - AL))))
# 降维,保证损失是是一个数,而不是一个矩阵/数组一样的东西
cost = np.squeeze(cost)
return cost
拿下边的代码来测试一下你写的是否正确吧!
Y, AL = compute_cost_test_case()
print("cost = " + str(compute_cost(AL, Y)))
我得到的结果如下:
cost = 0.41493159961539694
4.反向传播模块
如前向传播一样,你将要完善反向传播的函数。要记住反向传播是被用来计算损失函数的斜率从而更新函数的。
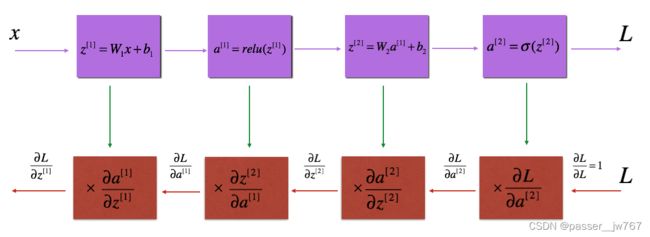
类似于前向传播,你建立反向传播一共有以下三步:
- LINEAR反向计算
- LINEAR -> ACTIVATION反向传播计算。且这个ACTIVATION用的是ReLU或Sgmoid的导数。
- 【LINEAR -> RELU】× (L-1)-> LINEAR -> SIGMOID(整个模型的流程)
4.1 线性反向传播
对于第L层,linear部分是这么计算的:
![]()
这一步后就是激活函数的计算了。
假设你已经计算了导数:
![]()
你想要得到
![]()
这些数。
我们通过一张图更直观的理解我们上边说的这些话。

三个输出(dW^ [l],db^ [l],dA^ [l])将通过dz^ [l]进行计算。这里有三个你可能需要用到的公式:

目标: 用上边给的三个公式来完成函数linear_backward(dZ, cache)。
其中:
- dZ:对于线性输出而言的成本梯度(当前层l)
- cache:含有(A_prev,W,b)元组,来自当前层的正向传播
需要返回(这里没翻译好,反正就是上边那张图中公式的意思):
- dA_prev:相对于激活函数而言的成本梯度(有着和A_prev一样的维度)
- dW:相对于W的梯度成本
- db:相对于b的梯度成本
由我们写的前向传播函数可以知道,cache中放的东西包括A、W、b。
def linear_backward(dZ, cache):
A_prev, W, b = cache
# W.shape[0]是本层的神经单元数
# W.shape[1]是上一层的神经单元数
# 只有在通过A = g(WX + b)的计算之后,得到的A的shape[1]才是数量
m = A_prev.shape[1]
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
dA_prev = np.dot(W.T, dZ)
assert (dW.shape == W.shape)
assert (dA_prev.shape == A_prev.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
直接复制下边的代码测试一下你的函数:
dZ, linear_cache = linear_backward_test_case()
dA_prev, dW, db = linear_backward(dZ, linear_cache)
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
结果为(这里我和原作者【学习链接2】出现了偏差(可能是种子有问题),我复制原作者的代码与此结果相同):
dA_prev = [[ 0.51822968 -0.19517421]
[-0.40506361 0.15255393]
[ 2.37496825 -0.89445391]]
dW = [[-0.10076895 1.40685096 1.64992505]]
db = 0.5062944750065832
4.2 线性激活函数的反向传播
接下来你需要写的函数包含了两个函数:linear_backward和激活函数的反向传播步骤linear_activation_backward。
为了帮助你完成linear_activation_backward,我们提供了两个反向函数给你。
- sigmoid_backward:完成Sigmoid单元的反向传播,你可以通过这样的形式调用它:dZ = sigmoid(dA, activation_cache)
- relu_backward:完成ReLU单元的反向传播,你可以通过这样的形式调用它:dZ = relu_backward(dA, activation_cache)
如果导数g(.)是激活函数,你可以使用sigomid_backward和relu_backward来计算:
![]()
目标: 完成LINEAR -> ACTIVATION层的反向传播。完成linear_activation_backward(dA, cache, activation)函数。
其中:
- dA:第l层激活后的梯度
- cache:含有(linear_cache,activation_cache)的元组,前边我们说到,存储它用于高效计算反向传播。我将在下边说明linear_cache和activation_cache。
- activation:是一个字符串,可能是“relu”,也可能是“sigmoid”
这里cache的来源是我们上边写过的一个函数linear_activation_forward(),我们写的这个函数是用于线性激活函数的正向传播。

1、linear_cache的来源就是linear_forward()函数。

由此可见,linear_cache包含的就是线性正向传播中的(A,W,b)
2、activation_cache的来源是sigmoid()和relu()函数。


由此看来,activation_cache实际上就是激活函数正向传播中的Z~
理解了以后,请根据公式大胆使用linear_cache和activation_cache吧!
要求返回:
- dA_prev:相对于前一层激活的梯度,有着和A_prev一样的维度
- dW:相对于W的梯度
- db:相对于b的梯度
def linear_activation_backward(dA, cache, activation):
linear_cache, activation_cache = cache
if activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
elif activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
有的人可能会有疑问,为什么cache里有linear_cache和activation_cache?这一点看一下正向传播时的linear_activation函数就知道了。
直接复制这段代码试试你的函数是否可行,若不可行,根据错误逐步修改:
AL, linear_activation_cache = linear_activation_backward_test_case()
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "sigmoid")
print ("sigmoid:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db) + "\n")
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "relu")
print ("relu:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
结果为(这里我和原作者【学习链接2】出现了偏差(可能是种子有问题),我复制原作者的代码与此结果相同):
sigmoid:
dA_prev = [[ 0.11017994 0.01105339]
[ 0.09466817 0.00949723]
[-0.05743092 -0.00576154]]
dW = [[ 0.10266786 0.09778551 -0.01968084]]
db = -0.057296222176291135
relu:
dA_prev = [[ 0.44090989 0. ]
[ 0.37883606 0. ]
[-0.2298228 0. ]]
dW = [[ 0.44513824 0.37371418 -0.10478989]]
db = -0.2083789237027353
4.3 反向传播L层模型
现在你将完善整个网络的反向传播函数。回顾当你完善L_model_forward函数,在每一次迭代过程中,你都存储了一个包含(X,W,b 和 z)的cache。在反向传播模块中,你将使用这些变量来计算斜率。因此,在L_model_backward函数中,你将从L层开始隐藏层的反向迭代。在每一步中,你将使用L层缓存中的值来进行反向传播。

初始化反向传播:通过这个网络进行反向传播,我们知道输出是这样的:
![]()
你的代码需要计算dAL,而dA^ [L]等于L对A^ [L]求导:
![]()
为了做到这一点,使用这个公式(这是使用微积分推导的,其实您不需要深入了解):
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) # derivative of cost with respect to AL
你可以使用这个激活函数斜率dAL持续进行反向传播。正如上边的图所看到的,您可以将dAL输入到已经实现的LINEAR->SIGMOID backward函数中(该函数将使用L_model_forward函数的缓存值)。
在这之后,你将使用一个for循环通过使用LINAER->RELU来迭代其它层。你将存储dA、dW和db在grads中。为了这么做,使用下面的代码:

例如,对于 L= 3,dW^ [l]会存储在grads[“dW3”]中。
目标: 完善【LINEAR -> RELU】× (L-1)-> LINEAR -> SIGMOID模型的反向传播函数L_model_backward(AL, Y, caches),其中:
- AL是可能性向量,是前向传播的输出(L_model_forward)
- Y是真实的“标签”向量(包括0-不是猫,1-是猫)
- caches:caches列表,包括如下信息:
每一个传入“ReLU”作为激活函数的linear_activation_forward()输出的缓存(caches[l],for l in range(L-1),i.e l = 0…L-2)
传入“Sigmoid”作为激活函数的linear_activation_forward()输出的缓存(caches[L-1])
应返回一个包含梯度信息的词典,如下:
- grads[“dA” + str(l)] = …
- grads[“dW” + str(l)] = …
- grads[“db” + str(l)] = …
请尝试写一写这个函数!
def L_model_backward(AL, Y, caches):
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L - 1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache,"sigmoid")
for l in reversed(range(L - 1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
(这个函数博主认为理解起来不容易。。所以将自己的理解贴在这里)
大概意思就是,在第L层前向传播时,使用的是sigmoid函数。所以在反向传播时就用的也是sigmoid的导数。
剩下的在L-1层以前(因为有很多层,所以使用了for循环,这个是没有办法向量化的),前向传播用的都是ReLU函数,所以这里反向传播使用的也是ReLU函数的导数来求解。
写好后,可以跑一下下边的代码验证你的函数:
AL, Y_assess, caches = L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dA1 = "+ str(grads["dA1"]))
结果为:
dW1 = [[0.41010002 0.07807203 0.13798444 0.10502167]
[0. 0. 0. 0. ]
[0.05283652 0.01005865 0.01777766 0.0135308 ]]
db1 = [-0.22007063 0. -0.02835349]
dA1 = [[ 0. 0.52257901]
[ 0. -0.3269206 ]
[ 0. -0.32070404]
[ 0. -0.74079187]]
5.更新参数
在这一部分,你将用梯度下降更新你模型中的参数:
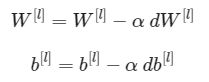
其中,α是学习率。在计算完更新参数后,将它们存储在参数字典中。
目标: 完成update_parameters()函数,使用梯度下降更新你的参数。
说明: 使用梯度下降更新每一个W^ [l]和b^ [l],l = 1,2,…,L
对于输入的参数:
- parameters:包括你所有参数的python字典
- grads:包括你梯度的python字典,是L_model_backward的输出
返回:
- grads:Python字典类型,包括你更新完的参数。
parameters[“W” + str(l)] = …
parameters[“b” + str(l)] = …
尝试写一下这个函数吧!
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
复制下边的代码试一试你的函数是否能够成功运行:
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)
print ("W1 = " + str(parameters["W1"]))
print ("b1 = " + str(parameters["b1"]))
print ("W2 = " + str(parameters["W2"]))
print ("b2 = " + str(parameters["b2"]))
结果如下:
W1 = [[-0.59562069 -0.09991781 -2.14584584 1.82662008]
[-1.76569676 -0.80627147 0.51115557 -1.18258802]
[-1.0535704 -0.86128581 0.68284052 2.20374577]]
b1 = [[-0.04659241]
[-1.28888275]
[ 0.53405496]]
W2 = [[-0.55569196 0.0354055 1.32964895]]
b2 = [[-0.84610769]]
四、概括
恭喜!你已经完成了所有建立一个深度神经网络所需要的函数!
我们都知道这很不容易,但是下半部分的任务就会简单许多
在下一个任务中,我们将会建立两个模型:
- 一个两层神经网络模型
- 一个L层神经网络模型
你将会实际运用这些模型来识别一张图片是猫/不是猫!
如果对本文章内容理解不深,建议多看几遍。
五、总代码
import numpy as np
import h5py
import matplotlib.pyplot as plt
from course1.week4.testCases import *
from course1.week4.dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
#
# plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
# plt.rcParams['image.interpolation'] = 'nearest'
# plt.rcParams['image.cmap'] = 'gray'
#
np.random.seed(1)
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(1)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def initialize_parameters_deep(layer_dims):
np.random.seed(3)
parameters = {}
L = len(layer_dims)
for i in range(1, L):
parameters["W" + str(i)] = np.random.randn(layer_dims[i], layer_dims[i - 1]) * 0.01
parameters["b" + str(i)] = np.zeros(shape=(layer_dims[i], 1))
assert (parameters["W" + str(i)].shape == (layer_dims[i], layer_dims[i - 1]))
assert (parameters["b" + str(i)].shape == (layer_dims[i], 1))
return parameters
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
def linear_activation_forward(A_prev, W, b, activation):
Z, linear_cache = linear_forward(A_prev, W, b)
if activation == "sigmoid":
A, activation_cache = sigmoid(Z)
elif activation == "relu":
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
def L_model_forward(X, parameters):
caches = []
A = X
# 每一层都应该有W和B两个参数,所以parameters//2就是层数
L = len(parameters) // 2
# 0-(L-1)层我们使用ReLU方法
for i in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev,
parameters["W" + str(i)],
parameters["b" + str(i)],
activation="relu")
caches.append(cache)
# 第L层(最后一层)我们使用sigmoid方法使最终结果处于0-1之间
AL, cache = linear_activation_forward(A,
parameters["W" + str(L)],
parameters["b" + str(L)],
activation="sigmoid")
caches.append(cache)
assert (AL.shape == (1, X.shape[1]))
# assert (AL.shape == (parameters["W" + str(L)].shape[0], X.shape[1]))
return AL, caches
def compute_cost(AL, Y):
# m,即数据集的大小,Y的大小是(1,m)
m = Y.shape[1]
# 根据公式写出损失函数
cost = -(1 / m) * (np.sum(np.multiply(Y, np.log(AL)) + np.multiply(1 - Y, np.log(1 - AL))))
# 降维,保证损失是是一个数,而不是一个矩阵/数组一样的东西
cost = np.squeeze(cost)
return cost
def linear_backward(dZ, cache):
A_prev, W, b = cache
# W.shape[0]是本层的神经单元数
# W.shape[1]是上一层的神经单元数
# 只有在通过A = g(WX + b)的计算之后,得到的A的shape[1]才是数量
m = A_prev.shape[1]
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
dA_prev = np.dot(W.T, dZ)
assert (dW.shape == W.shape)
assert (dA_prev.shape == A_prev.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
def linear_activation_backward(dA, cache, activation):
linear_cache, activation_cache = cache
if activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
elif activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
def L_model_backward(AL, Y, caches):
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L - 1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache,
"sigmoid")
for l in reversed(range(L - 1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters