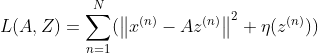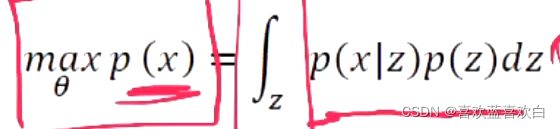无监督学习(含自编码器在MNIST上的图片重建实战)
目录
1. 无监督特征学习
1.1. PCA (主成分分析)
1.2. 稀疏编码
1.3. 自编码器
2. 自编码器在MNIST上的图片重建实战
3. 自编码器变种
3.1 稀疏自编码器
3.2. 堆叠自编码器
3.3. 降噪自编码器
3.4. 对抗自编码器
3.5. 变分自编码器
在现实应用中,机器学习的难点在于数据的标签难以获取。有时我们称这个工作为:数据标注工作。那有没有办法让机器来学习到数据本身的分布,是有的,我们称之为无监督学习。
无监督学习是指从无标签的数据中学习出一些有用的模式,即只有x。
无监督学习一般分为:
- 无监督特征学习:一般用来降维,数据可视化,或是数据预处理。
- 密度估计:根据一组样本来估计样本空间的概率密度。
- 聚类:将一组训练样本,根据不同的规则划分至不同的组里面。
1. 无监督特征学习
主要可分为:PCA、稀疏编码、自编码。
1.1. PCA (主成分分析)
是一种最常用的数据降维操作,使得在转换后的空间中的数据方差最大。假如现有一大堆东西其有很多成分构成,有些成分特别重要,有些则不。而我们需要做的工作就是把最重要的挖掘出来,所谓的降维就是将重要的特征取出来,然后特征的降低,即可以达到维度的降低。把高位数据集映射到低位空间中。
PCA一般会用来做数据预处理,但是PCA并不能一定提高模型的准确性,因为在降维的时候,就已经有一定的信息丢失。即通过降维提高准确性是不很可靠的。
因此PCA只是用在那种准确率本来就已经很高,我们可以使用PCA来实现模型的简化复杂度。对于太复杂的模型,PCA就可以实现即简单准确率又高。
那么我们是怎么将 N维向量降到R维,并且保留大部分的信息呢?
找到一条直线,使得两个特征的点在线上的产生映射,最后从二维降到一维。这条线的选取标准就是想让所有的点在线上的映射会足够的分散,即方差足够的大。
其他维度都是类似的。 先找第一个方向方差最大,之后找第二个方差最大。我们希望每个维度的信息相关性足够小,甚至完全不相关。即正交!
协方差可以表示两个维度的相关性,当协方差为0的时候就是正交,我们就说此时两变量是完全不相关的。
总结就是在每个维度内,我们都希望方差是最大的(即点足够分散),但是维度之间,我们希望协方差为0(即特征之间尽可能没有关系)。即我们要找到R个正交基。同时每个维度方差足够大。
如M*M -> N*M我们希望每行间的协方差=0,行内方差最大。
用这样一个矩阵来表示各行之间协方差的关系:
假设有一个原始矩阵:有一个X: M个N维的向量,原始协方差矩阵就是一个C: N*N的矩阵。我们需要的到一个Y : R*M的矩阵,它的协方差矩阵为:D : R*R。而协方差为0,就是希望对角线上的个每个元素(同一特征的而反差)都足够大,而其它元素(每个元素之间的反差)都是0.
实际上就是实现协方差矩阵的一个对角化。
对D做一个推导:
D = 1/M * Y * Y.T, Y = R * M, 则D = R*R。
我们需要一个变换矩阵:P(R,M)
1. 需要一个X (N*M)矩阵。
2. 01均值化。
3. 求出协方差矩阵C。
4. 求出协方差C的特征值(就是y每个元素的方差,从大到小沿对角线排列就可以构成D),和特征向量。
5. 将特征向量,按照特征量的大小排序,按实际需要,降维的多少,需要的数据量是多少,得到一个降维的矩阵p。
完整代码:
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
class DimensionValueError(ValueError):
"""定义异常类"""
pass
class PCA(object):
"""定义PCA类"""
# n_components 可是是自己选的降维后的维度,也可以是PCA算法自动算出来他认为最优的维度(若不填)
def __init__(self , x,n_components = None):
""""x的数据结构应为: (ids,features)"""
self.x = x
self.dimension = x.shape[1]
self.n_components = n_components
# 希望降维后的维度小于原有的维度
if n_components and n_components >= self.dimension:
return DimensionValueError("n_components error")
# x -> C
def cov(self):
"""求x的协方差矩阵"""
x_T = np.transpose(self.x) # 矩阵转置
x_cov = np.cov(x_T)
return x_cov
#C -> 特征值和特征向量
def get_feature(self):
"""求协方差矩阵C的特征值和特征向量"""
x_cov = self.cov()
a , b = np.linalg.eig(x_cov)
m = a.shape[0]
c = np.hstack((a.reshape((m,1)) , b)) # 得到特征值
c_df = pd.DataFrame(c)
c_df_sort = c_df.sort_values(0,ascending=False)
return c_df_sort
def explained_varience_(self):
c_df_sort = self.get_feature()
return c_df_sort.values[:,0]
def paint_varience_(self):
explained_varience_ = self.explained_varience_()
plt.figure()
plt.plot(explained_varience_,'k')
plt.xlabel('n_components',fontsize=16)
plt.xlabel('explained_varience_',fontsize=16)
plt.show()
def reduce_dimension(self):
"""根据指定维度降维/根据方差贡献率降维"""
c_df_sort = self.get_feature()
varience = self.explained_varience_()
if self.n_components:
p = c_df_sort.values[0:self.n_components,1:]
y = np.dot(p,np.transpose(self.X)) #矩阵叉乘
return np.transpose(y)
varience_sum = sum(varience) #利用反差贡献率来自动选择降维后维度
varience_radio = varience / varience_sum
varience_contribution = 0
for R in range(self.dimension):
varience_contribution += varience_radio[R] #前R个反差贡献之和
if varience_contribution >= 0.99: #前R个方差贡献度之和大于0.99,则认为前R个特征可以代表数据特征
break
p = c_df_sort.values[0:R + 1,1:] #取前R个特征维度
y = np.dot(p,np.transpose(self.x)) #矩阵叉乘
return np.transpose(y)
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x = tf.reshape(x_train,shape=(-1,784))
x.shape
if __name__ == '__main__':
pca = PCA(x)
y = pca.reduce_dimension()
print(y.shape)
pca.paint_varience_()1.2. 稀疏编码
我们人收到外界刺激真正只是一少部分的神经元,感受到的一直是少数的局部特征,具有稀疏性,首次启发。有人提出稀疏编码的模型。
线性编码:给定一组基向量A = [a1,a2……an],将输入样本x表示这些基向量的线性组合。
如输入一张图片28*28,共784个点,输入的维度就是784,基向量是p,编码就是对D维空间的x找到其在p维空间的一个表示。每个基向量之间是独立的。输入样本可以通过Z和a重构出来。所以编码的主要工作找到一个完备的基向量a,PCA也是其中一个方法。但是PCA得到的一个向量是稠密的,没有稀疏性。
为什么要强调稀疏性呢?就比如医生看病,也许生病有100种特征,医生诊断的时候只会根据几种来判断病因。但是这几种特征应该具有完备性。
完备性:
如果有p个基向量刚好能支撑p维的欧氏空间,则这p个向量是完备的。如果可支撑的维度d大于p的话,则这个基向量是过完备的。而稀疏编码得到目的是找到一组“超完备”的基向量来进行编码。
在此基础上,我们可以加入很多空的点,以此让他变得稀疏。
稀疏编码的目标函数:
我们怎么判断x输出的稀疏编码与x之间相差多少?最简单的方法之一就是l2范数。我们希望对应的稀疏编码Az能够尽量完全代表x。
稀疏性主要看![]() 部分,是个系数衡量函数,当越稀疏,他的值就越小。最直接简单的的就是l0范数,即非0元素的个数,但是其不连续不可导,所以我们可以使用l1范数,即所有数的绝对值之和。即越靠近0的向量,就越接近稀编码。
部分,是个系数衡量函数,当越稀疏,他的值就越小。最直接简单的的就是l0范数,即非0元素的个数,但是其不连续不可导,所以我们可以使用l1范数,即所有数的绝对值之和。即越靠近0的向量,就越接近稀编码。![]() 是个超参数。
是个超参数。
在整个公式中,我们不知道的是A和z。怎么求呢?训练过程是:
1. 固定基向量A,对每个输入的x,计算其对应的最优编码Z,即L(A,Z)为最小值的时候
2. 固定上一步的得到的编码向量Z1,Z2……Zn,计算器最优的基向量A。
稀疏编码的优点:
1. 降低计算量。
2. 可解释性,只有非常少数的非零元素,有生物的解释性。
3. 实现特征的自动选择,只选择和输入样本相关的最少特征,从而更好地表示输入呀昂本,降低噪声,并减轻过拟合。
1.3. 自编码器
PCA或是稀疏编码本质上都是一个线性变换。那能不能通过神经网络这样一个非线性的方式来实现呢?神经网络一般训练方式需要一个输入x,以及标签y。那我们可不可以利用输入本身作为一个监督信号,从而指导网络的训练呢?即用f(x) -> x。
为了实现这个目的,我们可以把网络分为两个部分:编码器,解码器。
编码器:是将x得到一个映射关系,也相当与一个将降维的过程。
解码器:是反过来得到与输入相同维度的向量。
当然二者之间可以有很多隐藏层。
2. 自编码器在MNIST上的图片重建实战
import tensorflow as tf
import numpy as np
from tensorflow import keras
import matplotlib.pyplot as plt
from PIL import Image
tf.__version__
image_size = 28*28
h_dim = 20
num_epochs = 50
batch_size = 100
learning_rate = 1e-3
new_im = Image.new('L',(280,280))
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train , x_test = x_train.astype(np.float32)/255. , x_test.astype(np.float32)/255.
train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(batch_size*5).batch(128).batch(batch_size)
test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = train_db.batch(batch_size)
class AE(keras.Model):
'''自编码器模型'''
def __init__(self):
super().__init__()
# 创建Encoder网络
self.encoder = keras.Sequential([
keras.layers.Dense(256,activation='relu'),
keras.layers.Dense(128,activation='relu'),
keras.layers.Dense(h_dim),
] , name='decoder')
# 创建Decoder网络
self.decoder = keras.Sequential([
keras.layers.Dense(128,activation='relu'),
keras.layers.Dense(256,activation='relu'),
keras.layers.Dense(image_size),
])
def call(self, inputs, training=None, mask=None):
# 编码
h = self.encoder(inputs)
# 解码
x_hat = self.decoder(h)
return x_hat
model = AE()
model.build(input_shape=(None,image_size))
model.summary()
for epoch in range(num_epochs):
for step, x in enumerate(train_db):
# step划分成批次的批次数,x就是[100,28,28]
x = tf.reshape(x, [-1,784])
with tf.GradientTape() as tape:
# 前向传播
x_reconstruction_logits = model(x) # 类似于通过前向传播求出的 预估值
# 计算loss
reconstruction_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x,logits=x_reconstruction_logits)
#对100张图片求出平均的loss
reconstruction_loss = tf.reduce_mean(reconstruction_loss)
# 自动求导
gradients = tape.gradient(reconstruction_loss ,model.trainable_variables)
# 自动更新
tf.optimizers.Adam(learning_rate).apply_gradients(zip(gradients,model.trainable_variables))
if epoch % 100 == 0:
print("epoch: ",epoch," step: ",step," loss: ",reconstruction_loss)
#每次迭代完成后,构建图片进行比较
out_logits = model(x[:batch_size//2])
out = tf.nn.sigmoid(out_logits)
out = tf.reshape(out, [-1,28,28]).numpy() * 255.
x = tf.reshape(x[:batch_size // 2], [-1,28,28])
x_concat = tf.concat( [x,out] ,axis = 0).numpy() * 255.
x_concat = x_concat.astype(np.uint8)
index = 0
for i in range(0,280,28):
for j in range(0,280,28):
im = x_concat[index]
im = Image.fromarray(im,mode='L')
new_im.paste(im,(i,j))
index += 1
new_im.save('images/_%d.png' % (epoch))
plt.imshow(np.asarray(new_im))
plt.show()
print('new image saved !')
# 取测试机中的一个批次的图片
x = next(iter(test_db))3. 自编码器变种
3.1 稀疏自编码器
给自编码器的隐藏层z上增加了稀疏性限制,希望编码层的输出维度大于输入的维度。
公式中的稀疏性限制ρ可以是KL散度。是神经元激活的概率。
3.2. 堆叠自编码器
通过逐层堆叠的方式训练一个深层的自编码器。
由于深层的网络会发生过拟合,以及参数量过大。我们就可以使用Droupout编码器,混合使用,来降低过拟合。
3.3. 降噪自编码器
给输入数据随即增加一些噪声,随机的将x的一些维度值设置为0,得到一个被破坏的向量x。
3.4. 对抗自编码器
通过任意先验分布与VAE隐藏代码向量的聚合后验匹配。将聚合后的后验与先验相匹配,确保从先验空间的任何部分产生的样本是有意义的。
原来的自编码器是实值与实值的比较,而变分自编码器,是将实值用概率值的方式考虑。实际上变分自编码器VAE是普通自编码器与贝叶斯模型的混合。
3.5. 变分自编码器
原来的自编码器,本质上是给定一个x,我们找到一个映射关系到Z。这本质上是一个判别模型,最后z解码后生成的x’本质上还是x生成的。那我们能不能通过隐藏的z来生产一个x‘呢?
可以从x得到隐变量z相应的一些概率分布。通过全概率分布p(x) = p(x|z)p(z),则可以得到一个p(x)的概率分布。
假设服从正态分布的Z,在生成器decoder的作用下,可以生成新的样本。那新的样本和原来的分布是否相等呢?
我们不能用KL散度来计算分布是否相等。
z(隐变量)可以理解为是有可能影响分布的一些可能性。生成的x肯定也会有一些z的特性
上述公式,假设p(z)是满足正态分布的,而p(x|z):即贝叶斯公式。
而公式中的p(z|x)可以用变分推断的方式,用一个q(z|x)来逼近,因为可以证明,总有方法使得一个映射到另一个概率分布。我们可以用KL散度来比较两种分布的差距。