3-1和3-2和3-3(nndl)
问题
证明在两类线性分类中,权重向量 w w w与决策平面正交。
解析
最头大的就是证明题了。 我们来看一下具体二分类的基本知识,从知识入手来寻找解决思路。在二分类问题中,我们需要一个线性判别函数 f ( x ; w ) = w T x + b f(x;w)=w^Tx+b f(x;w)=wTx+b特征空间中所有满足 f ( x ; w ) = 0 f(x;w)=0 f(x;w)=0的点组成一个分割超平面(Hyperplane),称为决策边界或决策平面。决策边界将特征空间一分为二,划分成两个区域,每个区域对应一个类别。我们想要证明上述问题只需要证明 w w w与决策平面中任意一个向量正交,对于超平面上的任意向量 x \boldsymbol{x} x由两点构成 x 1 , x 2 x_1,x_2 x1,x2∈ x \boldsymbol{x} x,
w T x 1 + b = 0 w^Tx_1+b=0 wTx1+b=0,
w T x 2 + b = 0 w^Tx_2+b=0 wTx2+b=0,
w T ( x 1 − x 2 ) = 0 w^T(x_1-x_2)=0 wT(x1−x2)=0即 w T x = 0 w^T\boldsymbol{x}=0 wTx=0可以推出 w ⊥ x w\bot \boldsymbol{x} w⊥x即权重向量 w w w与决策平面正交。
问题
在线性空间中,证明一个点 x x x到平面 f ( x : w ) = w T + b = 0 f(x:w)=w^T+b=0 f(x:w)=wT+b=0的距离为 ∣ f ( x ; w ) ∣ ∣ ∣ w ∣ ∣ \frac{|f\left( \boldsymbol{x;w} \right) |}{||\boldsymbol{w||}} ∣∣w∣∣∣f(x;w)∣
解析
下属解析来自nndl的课后题讨论,这里我就不再将其打成公式的形式。
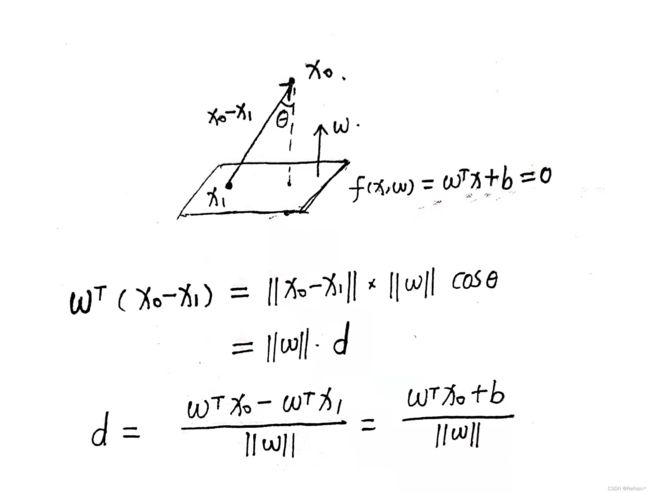
问题
在线性分类中,决策区域是凸的,即若点 x 1 x_1 x1和 x 2 x_2 x2被分为类别 c c c,则点 ρ x 1 + ( 1 − ρ ) x 2 \rho x_1+(1-\rho)x_2 ρx1+(1−ρ)x2也会被分为类别 c c c,其中 ρ ∈ ( 0 , 1 ) \rho∈(0,1) ρ∈(0,1)
解析
参照书上,线性分类可以分为二分类和多分类,所以我们从这两个方面来着手进行证明。
二分类证明:
两类线性可分:对于训练集 D = { ( x ( n ) , y ( n ) ) } n = 1 N \mathcal{D}=\left\{ \left( x^{\left( n \right)},y^{\left( n \right)} \right) \right\} _{n=1}^{N} D={(x(n),y(n))}n=1N,如果存在权重向量 w ∗ w^* w∗,对所有样本都是满足 y f ( x ; w ∗ ) > 0 yf(x;w^*)>0 yf(x;w∗)>0,那么训练集 D \mathcal{D} D是线性可分的。
对于二分类来说
假设 x 1 , x 2 x_1,x_2 x1,x2都被分类为正类,即 y 1 , y 2 = 1 y_1,y_2=1 y1,y2=1并且假设 x 1 > x 2 x_1>x_2 x1>x2因此有如下:
y 1 ( w T x 1 + b ) > 0 ⇒ w T x 1 + b > 0 y_1\left( w^Tx_1+b \right) >0\Rightarrow w^Tx_1+b>0 y1(wTx1+b)>0⇒wTx1+b>0
y 2 ( w T x 2 + b ) > 0 ⇒ w T x 2 + b > 0 y_2\left( w^Tx_2+b \right) >0\Rightarrow w^Tx_2+b>0 y2(wTx2+b)>0⇒wTx2+b>0
w T ( x 1 − x 2 ) > 0 w^T\left( x_1-x_2 \right) >0 wT(x1−x2)>0
将点代入得:
w T ( ρ x 1 + ( 1 − ρ ) x 2 ) + b w^T\left( \rho x_1+\left( 1-\rho \right) x_2 \right) +b wT(ρx1+(1−ρ)x2)+b
= ρ w T x 1 + w T x 1 + ( 1 − ρ ) w T x 2 + b =\rho w^Tx_1+w^Tx_1+\left( 1-\rho \right) w^Tx_2+b =ρwTx1+wTx1+(1−ρ)wTx2+b
= w T ( x 1 + x 2 ) + ρ w T ( x 1 − x 2 ) + b > 0 =w^T\left( x_1+x_2 \right) +\rho w^T\left( x_1-x_2 \right) +b>0 =wT(x1+x2)+ρwT(x1−x2)+b>0
所以 ρ \rho ρ x 1 + ( 1 − ρ ) x 2 x_1+(1-\rho)x_2 x1+(1−ρ)x2也会被分为正类
对于多分类问题:
多类线性可分:对于训练集 D = { ( x ( n ) , y ( n ) ) } n = 1 N D=\left\{ \left( x^{\left( n \right)},y^{\left( n \right)} \right) \right\} _{n=1}^{N} D={(x(n),y(n))}n=1N,如果存在 C C C个权重向量 w 1 ∗ , ⋅ ⋅ ⋅ , w C ∗ w_{1}^{*},···,w_{C}^{*} w1∗,⋅⋅⋅,wC∗使得 c ( 1 ≤ c ≤ C ) c(1\le c\le C) c(1≤c≤C)类的所有样本都满足 f c ( x ; w c ∗ ) > f c ˉ ( x , w c ∗ ) , ∀ c ˉ ≠ c f_c\left( x;w_{c}^{*} \right) >f_{\bar{c}}\left( x,w_{c}^{*} \right) ,\forall \bar{c}\ne c fc(x;wc∗)>fcˉ(x,wc∗),∀cˉ=c,那么训练集 D D D是线性可分的。
我们利用多分类的定义来证明如下:
点 x 1 , x 2 x_1,x_2 x1,x2被分为类别 c c c则说明:
f c ( x 1 ; w c ∗ ) > f c ˉ ( x 1 , w c ∗ ) f c ( x 1 ; w c ∗ ) > f c ˉ ( x 1 , w c ∗ ) \ \ \ \ f_c\left( x_1;w_{c}^{*} \right) >f_{\bar{c}}\left( x_1,w_{c}^{*} \right) \ \ \ \ \ \ \ f_c\left( x_1;w_{c}^{*} \right) >f_{\bar{c}}\left( x_1,w_{c}^{*} \right) fc(x1;wc∗)>fcˉ(x1,wc∗) fc(x1;wc∗)>fcˉ(x1,wc∗)
即: f c ( x 1 ; w c ∗ ) − f c ˉ ( x 1 , w c ∗ ) > 0 f c ( x 1 ; w c ∗ ) − f c ˉ ( x 1 , w c ∗ ) > 0 \text{即:}f_c\left( x_1;w_{c}^{*} \right) -f_{\bar{c}}\left( x_1,w_{c}^{*} \right) >0\ \ \ \,\,f_c\left( x_1;w_{c}^{*} \right) -f_{\bar{c}}\left( x_1,w_{c}^{*} \right) >0 即:fc(x1;wc∗)−fcˉ(x1,wc∗)>0 fc(x1;wc∗)−fcˉ(x1,wc∗)>0
即: w c T x 1 + b c − w c ˉ T x 1 − b c ˉ > 0 w c T x 2 + b c − w c ˉ T x 2 − b c > 0 \text{即:}w_{c}^{T}x_1+b_c-w_{\bar{c}}^{T}x_1-b_{\bar{c}}>0\ \ \ \ \ w_{c}^{T}x_2+b_c-w_{\bar{c}}^{T}x_2-b_c>0 即:wcTx1+bc−wcˉTx1−bcˉ>0 wcTx2+bc−wcˉTx2−bc>0
将 ρ x 1 + ( 1 − ρ ) x 2 带入: \text{将}\rho x_1+\left( 1-\rho \right) x_2\text{带入:} 将ρx1+(1−ρ)x2带入:
ρ ( w c T x 1 + b c − w c ˉ T x 1 − b c ˉ ) > 0 ( 1 − ρ ) ( w c T x 2 + b c − w c ˉ T x 2 − b c ) > 0 \rho \left( w_{c}^{T}x_1+b_c-w_{\bar{c}}^{T}x_1-b_{\bar{c}} \right) >0\ \ \ \left( 1-\rho \right) \left( w_{c}^{T}x_2+b_c-w_{\bar{c}}^{T}x_2-b_c \right) >0 ρ(wcTx1+bc−wcˉTx1−bcˉ)>0 (1−ρ)(wcTx2+bc−wcˉTx2−bc)>0
ρ ( w c T x 1 + b c − w c ˉ T x 1 − b c ˉ ) + ( 1 − ρ ) ( w c T x 2 + b c − w c ˉ T x 2 − b c ) > 0 \rho \left( w_{c}^{T}x_1+b_c-w_{\bar{c}}^{T}x_1-b_{\bar{c}} \right) +\left( 1-\rho \right) \left( w_{c}^{T}x_2+b_c-w_{\bar{c}}^{T}x_2-b_c \right) >0 ρ(wcTx1+bc−wcˉTx1−bcˉ)+(1−ρ)(wcTx2+bc−wcˉTx2−bc)>0
化简得: \text{化简得:} 化简得:
w c T ( ρ x 1 + ( 1 − ρ ) x 2 ) + b c − w c ˉ T ( ρ x 1 + ( 1 − ρ ) x 2 ) > 0 w_{c}^{T}\left( \rho x_1+\left( 1-\rho \right) x_2 \right) +b_c-w_{\bar{c}}^{T}\left( \rho x_1+\left( 1-\rho \right) x_2 \right) >0 wcT(ρx1+(1−ρ)x2)+bc−wcˉT(ρx1+(1−ρ)x2)>0
即 f c ( ρ x 1 + ( 1 − ρ ) x 2 ; w c ∗ ) > f c ˉ ( ρ x 1 + ( 1 − ρ ) x 2 , w c ∗ ) \text{即}f_c\left( \rho x_1+\left( 1-\rho \right) x_2;w_{c}^{*} \right) >f_{\bar{c}}\left( \rho x_1+\left( 1-\rho \right) x_2,w_{c}^{*} \right) \,\,\,\, 即fc(ρx1+(1−ρ)x2;wc∗)>fcˉ(ρx1+(1−ρ)x2,wc∗)
所以点 ρ x 1 + ( 1 − ρ ) x 2 \rho x_1+\left( 1-\rho \right) x_2 ρx1+(1−ρ)x2也会被分为类别 c c c