Java实现二叉搜索树的插入、删除功能

二叉树的结构

public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {
        }
        TreeNode(int val) {
            this.val = val;
        }
    }

中序遍历

• 中序遍历：从根节点开始遍历，遍历顺序是：左子树->当前节点->右子树，在中序遍历中，对每个节点来说：

只有当它的左子树都被遍历过了（或者没有左子树），它才会被遍历到。
在遍历右子树之前，一定会先遍历当前节点。

• 中序遍历得到的第一个节点是没有左子树的（也许是叶子节点，也许有右子树）
• 同理，中序遍历的最后一个节点没有右子树

代码递归实现

List list = new ArrayList<>();
    public void inorder_traversal(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left != null) {
            inorder_traversal(root.left);
        }
        list.add(root);
        if (root.right != null) {
            inorder_traversal(root.right);
        }
    }

二叉搜索树的定义

• 对每一个节点而言，左子树的所有节点小于它，右子树的所有节点大于它
• 二叉树中每一个节点的值都不相同
• 中序遍历的结果是升序的

这些定义决定了它的优点：查找效率快，因为二叉搜索树查找一个值时，可以通过二分查找的方式，平均时间复杂度为log2(n),n是二叉树的层树

下图就是一个标准的二叉搜索树，右子树比根节点大，左子树比根节点小

查找节点

给定一个值，使用循环在二叉搜索树中查找，找到该节点为止

• 从根节点开始，不断循环进行比较
• 给定值大于当前节点，就找右子树，小于就找左子树，值相等就是找到了节点

代码实现如下

public TreeNode search(TreeNode root, int val) {
        // 节点不为空，且不等于特定值
        while(root != null && root.val != val){
            if(root.val > val){
                root = root.left;
            }else{
                root = root.right;
            }
        }
        return root;
    }

添加节点

设要添加的节点为b， 二叉搜索树的添加是将b作为叶子节点加入到其中，因为叶子节点的增加比较简单。

• 跟搜索过程类似，从根节点开始，不断循环找，找到一个适合新节点的位置

b值比当前节点大（小），并且当前节点的右（左）子树为空，将b插入到当前节点的右（左）子树中
如果当前节点的子树不为空，继续往下寻找

• 使用一个随着搜索过程，不断更新的pre节点作为b的父节点，由pre节点添加b
• 有可能要插入节点的二叉树是一颗空树，创建一个新的二叉树
• 如果二叉搜索树中已经有跟b相等的值，不需要进行添加

 public TreeNode insertInto(TreeNode root, int val) {
        
        if (root == null) {
            // 树为空树的情况
            return new TreeNode(val);
        }
        // 一个临时节点指向根节点，用于返回值
        TreeNode tmp = root;
        TreeNode pre = root;
        
        while (root != null && root.val != val) {
            // 保存父节点
            pre = root;
            if (val > root.val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        // 通过父节点添加
        if (val > pre.val) {
            pre.right = new TreeNode(val);
        } else {
            pre.left = new TreeNode(val);
        }
        return tmp;
    }

删除节点

删除过程比较复杂，先设二叉搜索树要删除的节点为a，a有以下三种情况

• a为叶子节点
• a有一个子节点
• a有两个子节点删除叶子节点

过程类似搜索节点，找到到a后，通过它的父节点删除，并且叶子节点的删除不影响树的性质

有一个子节点的节点

要将a删除，并且保留a的子节点，让它的父节点连接它的子节点即可，因为a的子节点 与 a的父节点 关系 == a与 a的父节点 关系，所以不改变树的性质

• 二叉搜索树的定义决定了：对于每一个节点而言，它 大于（小于） 它的父节点，那么它的子节点 大于（小于） 它的父节点

过程像这张图一样

删除有两个子节点的节点

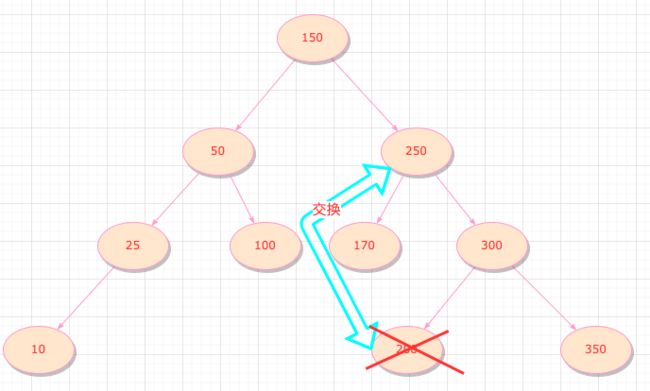
我们可以通过交换节点的方式，让a 和 只有一个子节点的节点 交换，删除a的操作就变成了上面第二种情况。

我们知道中序遍历二叉搜索树的结果是升序的，如果要交换，肯定要找中序遍历在a左右两边的节点（因为值交换之后也满足二叉搜索树的定义）

• 中序遍历的后（前）一个节点是右（左）子树中序遍历的第一个（最后一个）节点，而且它们都只有一个子节点

过程跟下面这张图类似（a的值与中序遍历的后一个节点交换，并删除这个节点）

代码实现

public TreeNode deleteNode(TreeNode root, int key) {
        TreeNode tmp = root;
        TreeNode pre = root;
        // 寻找要删除的节点
        while (root != null && root.val != key) {
            pre = root;
            if (key > root.val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        // 找不到符合的节点值
        if (root == null) {
            return tmp;
        }
        // 只有一个子节点或者没有子节点的情况
        if (root.left == null || root.right == null) {
            if (root.left == null) {
                // 要删除的是根节点，返回它的子节点
                if (root == tmp) {
                    return root.right;
                }
                // 使用父节点连接子节点，实现删除当前节点
                if (pre.left == root) {
                    pre.left = root.right;
                } else {
                    pre.right = root.right;
                }
            } else {
                if (root == tmp) {
                    return root.left;
                }
                if (pre.left == root) {
                    pre.left = root.left;
                } else {
                    pre.right = root.left;
                }
            }
            return tmp;
        }
        // 第一种方式
        // 寻找中序遍历的后一个节点，也就是右子树进行中序遍历的第一个节点，右子树的最左节点
        pre = root;
        TreeNode rootRight = root.right;
        while (rootRight.left != null) {
            pre = rootRight;
            rootRight = rootRight.left;
        }
        // 节点的值进行交换
        int tmpVal = rootRight.val;
        rootRight.val = root.val;
        root.val = tmpVal;
        // 中序遍历的第一个节点肯定是没有左子树的，但是可能有右子树，将右子树连接到父节点上（相当于删除有一个子节点的节点）
        if (pre.left == rootRight) {
            pre.left = rootRight.right;
        }else {
            pre.right = rootRight.right;
        }
        // 第二种方式
        // 寻找中序遍历的前一个节点，也就是左子树进行中序遍历的最后一个节点，左子树的最右节点
//        pre = root;
//        TreeNode rootLeft = root.left;
//        while (rootLeft.right != null){
//            pre = rootLeft;
//            rootLeft = rootLeft.right;
//        }
//
//        int tmpVal = rootLeft.val;
//        rootLeft.val = root.val;
//        root.val = tmpVal;
//
//        // 中序遍历的最后一个节点肯定是没有右子树的，但是可能有左子树，将左子树连接到父节点上（相当于删除有一个子节点的节点）
//        if (pre.left == rootLeft) {
//            pre.left = rootLeft.left;
//        }else {
//            pre.right = rootLeft.left;
//        }
        return tmp;
    }

到此这篇关于Java实现二叉搜索树的插入、删除的文章就介绍到这了,更多相关Java二叉搜索树内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！