【C++】图像处理中的微分算子原理与实现
图像处理中的微分算子原理与实现
一阶微分边缘算子:经典算子比如:Roberts(罗伯特)、Prewitt(普鲁伊特)、Sobel(索贝尔),Canny(坎尼)等。
二阶微分边缘算子:Laplacian算子,LoG( Laplace of Gaussian function)边缘检测算子和DoG(Difference of Gaussian)高斯差分算子。

-
Roberts算子
1963年,Roberts算子,又称罗伯茨算子,是一种最简单的算子,是一种利用局部差分算子寻找边缘的算子。他采用对角线方向相邻两象素之差近似梯度幅值检测边缘。检测垂直边缘的效果好于斜向边缘,定位精度高,对噪声敏感,无法抑制噪声的影响。
Roberts算子的模板分为水平方向和垂直方向,如下式所示,从其模板可以看出,Roberts算子能较好的增强正负45度的图像边缘。
![]()
void quick_opencv::roberts_Demo(Mat &img)
{
// Roberts算子边缘检测
cvtColor(img,img,COLOR_BGR2GRAY);
Mat grad;
grad.create(img.size(), CV_8UC1);
for (int i = 1; i < img.rows - 1; i++)
{
for (int j = 1; j < img.cols - 1; j++)
{
grad.at<uchar>(i, j) = saturate_cast<uchar>(fabs(img.at<uchar>(i, j) - img.at<uchar>(i - 1, j - 1)) + fabs(img.at<uchar>(i, j - 1) - img.at<uchar>(i - 1, j)));
}
}
imshow("Roberts算子", grad);
}
-
Prewitt算子
1970年,Prewitt算子来自J.M.S. Prewitt “Object Enhancement and Extraction” in “Picture processing and Psychopictorics”, Academic Press
Prewitt算子是一种图像边缘检测的微分算子,其原理是利用特定区域内像素灰度值产生的差分实现边缘检测。由于Prewitt算子采用 33 模板对区域内的像素值进行计算,而Robert算子的模板为 22,故Prewitt算子的边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。Prewitt算子适合用来识别噪声较多、灰度渐变的图像,其计算公式如下所示:

void getPrewitt_oper(Mat& getPrewitt_horizontal, Mat& getPrewitt_vertical, Mat& getPrewitt_Diagonal1, Mat& getPrewitt_Diagonal2) {
//水平方向
getPrewitt_horizontal = (Mat_<float>(3, 3) << -1, -1, -1, 0, 0, 0, 1, 1, 1);
//垂直方向
getPrewitt_vertical = (Mat_<float>(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1);
//对角135°
getPrewitt_Diagonal1 = (Mat_<float>(3, 3) << 0, 1, 1, -1, 0, 1, -1, -1, 0);
//对角45°
getPrewitt_Diagonal2 = (Mat_<float>(3, 3) << -1, -1, 0, -1, 0, 1, 0, 1, 1);
//逆时针反转180°得到卷积核
flip(getPrewitt_horizontal, getPrewitt_horizontal, -1);
flip(getPrewitt_vertical, getPrewitt_vertical, -1);
flip(getPrewitt_Diagonal1, getPrewitt_Diagonal1, -1);
flip(getPrewitt_Diagonal2, getPrewitt_Diagonal2, -1);
}
void edge_Prewitt(Mat& src, Mat& dst1, Mat& dst2, Mat& dst3, Mat& dst4, Mat& dst, int ddepth, double delta = 0, int borderType = BORDER_DEFAULT) {
//获取Prewitt算子
Mat getPrewitt_horizontal;
Mat getPrewitt_vertical;
Mat getPrewitt_Diagonal1;
Mat getPrewitt_Diagonal2;
getPrewitt_oper(getPrewitt_horizontal, getPrewitt_vertical, getPrewitt_Diagonal1, getPrewitt_Diagonal2);
//卷积得到水平方向边缘
filter2D(src, dst1, ddepth, getPrewitt_horizontal, Point(-1, -1), delta, borderType);
//卷积得到4垂直方向边缘
filter2D(src, dst2, ddepth, getPrewitt_vertical, Point(-1, -1), delta, borderType);
//卷积得到45°方向边缘
filter2D(src, dst3, ddepth, getPrewitt_Diagonal1, Point(-1, -1), delta, borderType);
//卷积得到135°方向边缘
filter2D(src, dst4, ddepth, getPrewitt_Diagonal2, Point(-1, -1), delta, borderType);
//边缘强度(近似)
convertScaleAbs(dst1, dst1); //求绝对值并转为无符号8位图
convertScaleAbs(dst2, dst2);
convertScaleAbs(dst3, dst3); //求绝对值并转为无符号8位图
convertScaleAbs(dst4, dst4);
dst = dst1 + dst2;
}
void quick_opencv::prewitt_Demo(Mat &img)
{
Mat dst, dst1, dst2, dst3, dst4;
cvtColor(img, img, COLOR_BGR2GRAY);
//注意:要采用CV_32F,因为有些地方卷积后为负数,若用8位无符号,则会导致这些地方为0
edge_Prewitt(img, dst1, dst2, dst3, dst4, dst, CV_32F);
namedWindow("水平边缘", WINDOW_NORMAL);
imshow("水平边缘", dst1);
namedWindow("垂直边缘", WINDOW_NORMAL);
imshow("垂直边缘", dst2);
namedWindow("45°边缘", WINDOW_NORMAL);
imshow("45°边缘", dst3);
namedWindow("135°边缘", WINDOW_NORMAL);
imshow("135°边缘", dst4);
namedWindow("边缘强度", WINDOW_NORMAL);
imshow("边缘强度", dst);
}
-
Sobel算子
1973年,Sobel边缘算子,当年作者并没有公开发表过论文,仅仅是在一次博士生课题讨论会(1968)上提出(“A 3x3 Isotropic Gradient Operator for Image Processing”),后在1973年出版的一本专著(“Pattern Classification and Scene Analysis”)的脚注里作为注释出现和公开的。
Sobel算子是一种用于边缘检测的离散微分算子,它结合了高斯平滑和微分求导。该算子用于计算图像明暗程度近似值,根据图像边缘旁边明暗程度把该区域内超过某个数的特定点记为边缘。Sobel算子在Prewitt算子的基础上增加了权重的概念,认为相邻点的距离远近对当前像素点的影响是不同的,距离越近的像素点对应当前像素的影响越大,从而实现图像锐化并突出边缘轮廓。
Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息。因为Sobel算子结合了高斯平滑和微分求导(分化),因此结果会具有更多的抗噪性,当对精度要求不是很高时,Sobel算子是一种较为常用的边缘检测方法。
Sobel算子的边缘定位更准确,常用于噪声较多、灰度渐变的图像。其算法模板如下面的公式所示,其中 表示水平方向, 表示垂直方向。

void quick_opencv::sobel_Demo(Mat &img)
{
cvtColor(img, img, COLOR_BGR2GRAY);
Mat imageX = Mat::zeros(img.size(), CV_16SC1);
Mat imageY = Mat::zeros(img.size(), CV_16SC1);
Mat imageXY = Mat::zeros(img.size(), CV_16SC1);
Mat imageX8UC;
Mat imageY8UC;
Mat imageXY8UC;
GaussianBlur(img, img, Size(3, 3), 0); //高斯滤波器(模糊/平滑/近似)消除噪点
uchar *P = img.data;
uchar *PX = imageX.data;
uchar *PY = imageY.data;
int step = img.step;
int stepXY = imageX.step;
for (int i = 1;i < img.rows - 1;i++)
{
for (int j = 1;j < img.cols - 1;j++)
{
// 通过指针遍历图像上每一个像素
// 求出X,Y方向的导数(梯度) sobel算子加权的结果
PX[i*imageX.step + j * (stepXY / step)] = abs(P[(i - 1)*step + j + 1] + P[i*step + j + 1] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[i*step + j - 1] * 2 - P[(i + 1)*step + j - 1]);
PY[i*imageX.step + j * (stepXY / step)] = abs(P[(i + 1)*step + j - 1] + P[(i + 1)*step + j] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[(i - 1)*step + j] * 2 - P[(i - 1)*step + j + 1]);
}
}
addWeighted(imageX, 0.5, imageY, 0.5, 0, imageXY);//融合X、Y方向的梯度
convertScaleAbs(imageX, imageX8UC);
convertScaleAbs(imageY, imageY8UC);
convertScaleAbs(imageXY, imageXY8UC); //转换为8bit图像
Mat imageSobel;
Mat x_grad, y_grad;
Sobel(img, x_grad, CV_16S, 1, 0, 3);
Sobel(img, y_grad, CV_16S, 0, 1, 3);
convertScaleAbs(x_grad, x_grad);
convertScaleAbs(y_grad, y_grad);
addWeighted(x_grad, 0.5, y_grad, 0.5, 0, imageSobel);
imshow("Source Image", img);
imshow("X Direction", imageX8UC);
imshow("Y Direction", imageY8UC);
imshow("XY Direction", imageXY8UC);
imshow("Opencv Soble", imageSobel);
}
-
Canny算子
1986年,Canny边缘检测算子是John F. Canny开发出来的一个多级边缘检测算法。更为重要的是Canny创立了“边缘检测计算理论”(computational theory of edge detection)解释这项技术如何工作。到今天已经30多年过去了,但Canny算法仍然是图像边缘检测算法中最经典、先进的算法之一。
1、高斯平滑
2、计算梯度幅度和方向
可选用的模板:soble算子、Prewitt算子、Roberts模板等等;
一般采用soble算子,OpenCV也是如此,利用soble水平和垂直算子与输入图像卷积计算dx、dy
3、根据角度对幅值进行非极大值抑制
沿着梯度方向对幅值进行非极大值抑制,而非边缘方向
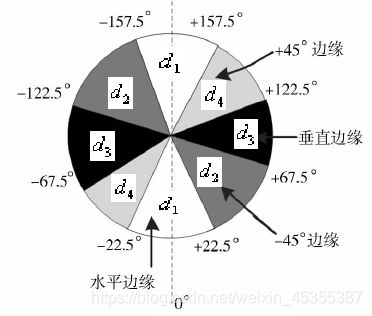
在每一点上,领域中心 x 与沿着其对应的梯度方向的两个像素相比,若中心像素为最大值,则保留,否则中心置0,这样可以抑制非极大值,保留局部梯度最大的点,以得到细化的边缘。
4、用双阈值算法检测和连接边缘
选取系数TH和TL,比率为2:1或3:1。(一般取TH=0.3或0.2,TL=0.1);
将小于低阈值的点抛弃,赋0;将大于高阈值的点立即标记(这些点为确定边缘点),赋1或255;
将小于高阈值,大于低阈值的点使用8连通区域确定(即:只有与TH像素连接时才会被接受,成为边缘点,赋 1或255)
void quick_opencv::canny_Demo(Mat &img)
{
ConvertRGB2GRAY(img, imageGray); //RGB转换为灰度图
imshow("Gray Image", imageGray);
int size = 5; //定义卷积核大小
double **gaus = new double *[size]; //卷积核数组
for (int i = 0;i < size;i++)
{
gaus[i] = new double[size]; //动态生成矩阵
}
GetGaussianKernel(gaus, 5, 1); //生成5*5 大小高斯卷积核,Sigma=1;
imageGaussian = Mat::zeros(imageGray.size(), CV_8UC1);
GaussianFilter(imageGray, imageGaussian, gaus, 5); //高斯滤波
imshow("Gaussian Image", imageGaussian);
Mat imageSobelY;
Mat imageSobelX;
double *pointDirection = new double[(imageSobelX.cols - 1)*(imageSobelX.rows - 1)]; //定义梯度方向角数组
SobelGradDirction(imageGaussian, imageSobelX, imageSobelY, pointDirection); //计算X、Y方向梯度和方向角
imshow("Sobel Y", imageSobelY);
imshow("Sobel X", imageSobelX);
Mat SobelGradAmpl;
SobelAmplitude(imageSobelX, imageSobelY, SobelGradAmpl); //计算X、Y方向梯度融合幅值
imshow("Soble XYRange", SobelGradAmpl);
Mat imageLocalMax;
LocalMaxValue(SobelGradAmpl, imageLocalMax, pointDirection); //局部非极大值抑制
imshow("Non-Maximum Image", imageLocalMax);
Mat cannyImage;
cannyImage = Mat::zeros(imageLocalMax.size(), CV_8UC1);
DoubleThreshold(imageLocalMax, 90, 160); //双阈值处理
imshow("Double Threshold Image", imageLocalMax);
DoubleThresholdLink(imageLocalMax, 90, 160); //双阈值中间阈值滤除及连接
imshow("Canny Image", imageLocalMax);
}
-
Laplace算子
1812年,拉普拉斯(Laplace, 1749 – 1827)发表了重要的《概率分析理论》一书,在该书中总结了当时整个概率论的研究,论述了概率在选举审判调查、气象等方面的应用,导入「拉普拉斯变换」等。
拉普拉斯(Laplacian) 算子是 维欧几里德空间中的一个二阶微分算子,常用于图像增强领域和边缘提取。它通过灰度差分计算邻域内的像素。
算法基本流程
1)判断图像中心像素灰度值与它周围其他像素的灰度值,如果中心像素的灰度更高,则提升中心像素的灰度;反之降低中心像素的灰度,从而实现图像锐化操作;
2)在算法实现过程中,Laplacian算子通过对邻域中心像素的四方向或八方向求梯度,再将梯度相加起来判断中心像素灰度与邻域内其他像素灰度的关系;
3)最后通过梯度运算的结果对像素灰度进行调整。
Laplacian算子分为四邻域和八邻域,四邻域是对邻域中心像素的四个方向求梯度,八邻域是对八个方向求梯度。
其中,Laplacian算子四邻域模板如下所示:
Laplacian算子的八邻域模板如下所示:

通过Laplacian算子的模板可以发现:
1)当邻域内像素灰度相同时,模板的卷积运算结果为0;
2)当中心像素灰度高于邻域内其他像素的平均灰度时,模板的卷积运算结果为正数;
3)当中心像素的灰度低于邻域内其他像素的平均灰度时,模板的卷积为负数。对卷积运算的结果用适当的衰弱因子处理并加在原中心像素上,就可以实现图像的锐化处理。
void quick_opencv::laplacian_Demo(Mat &img)
{
Mat src_gray;
int kernel_size = 3;
const char* window_name = "Laplacian Demo";
cvtColor(img, src_gray, COLOR_RGB2GRAY);
namedWindow(window_name, WINDOW_AUTOSIZE);
Mat dst, abs_dst;
Laplacian(src_gray, dst, CV_16S, kernel_size);
convertScaleAbs(dst, abs_dst);
imshow(window_name, abs_dst);
}
-
LoG算子
1980年,LoG边缘检测算子是David Courtnay Marr和Ellen Hildreth共同提出的,因此,也称为Marr & Hildreth 边缘检测算法或Marr & Hildreth算子。该算法首先对图像做高斯滤波,然后再求其拉普拉斯(Laplacian)二阶导数。即图像与 Laplacian of the Gaussian function 进行滤波运算。最后,可以通过检测滤波结果的零交叉(Zero crossings)获得图像或物体的边缘。因而,也被业界简称为Laplacian-of-Gaussian (LoG)算子。Log算子的表达式如下:![]()
常用的卷积模板是5*5的模板:
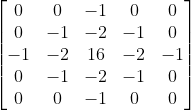
void quick_opencv::LOG_Demo(Mat &img)
{
//高斯-拉普拉斯算子 二阶微分 用于边缘检测
Mat src_gray;
int kernel_size = 3;
const char* window_name = "LOG Demo";
GaussianBlur(img, img, Size(3, 3), 0, 0, BORDER_DEFAULT);
cvtColor(img, src_gray, COLOR_RGB2GRAY);
namedWindow(window_name, WINDOW_AUTOSIZE);
Mat dst, abs_dst;
Laplacian(src_gray, dst, CV_16S, kernel_size);
convertScaleAbs(dst, abs_dst);
imshow(window_name, abs_dst);
}
-
DoG算子
1980年,高斯差分(DoG)算子,Marr and Hildreth指出,使用高斯差分(DOG)来近似Log算子是可能的:
![]()
LoG算子和DoG算子的函数波形对比如下图所示,由于高斯差分的计算更加简单,因此可用DoG算子近似替代LoG算子:

//x,y方向联合实现获取高斯模板
void generateGaussMask(Mat& Mask, Size wsize, double sigma) {
Mask.create(wsize, CV_64F);
int h = wsize.height;
int w = wsize.width;
int center_h = (h - 1) / 2;
int center_w = (w - 1) / 2;
double sum = 0.0;
double x, y;
for (int i = 0; i < h; ++i) {
y = pow(i - center_h, 2);
for (int j = 0; j < w; ++j) {
x = pow(j - center_w, 2);
//因为最后都要归一化的,常数部分可以不计算,也减少了运算量
double g = exp(-(x + y) / (2 * sigma*sigma));
Mask.at<double>(i, j) = g;
sum += g;
}
}
Mask = Mask / sum;
}
//按二维高斯函数实现高斯滤波
void GaussianFilter(Mat& src, Mat& dst, Mat window) {
int hh = (window.rows - 1) / 2;
int hw = (window.cols - 1) / 2;
dst = Mat::zeros(src.size(), src.type());
//边界填充
Mat Newsrc;
copyMakeBorder(src, Newsrc, hh, hh, hw, hw, BORDER_REPLICATE);//边界复制
//高斯滤波
for (int i = hh; i < src.rows + hh; ++i) {
for (int j = hw; j < src.cols + hw; ++j) {
double sum[3] = { 0 };
for (int r = -hh; r <= hh; ++r) {
for (int c = -hw; c <= hw; ++c) {
if (src.channels() == 1) {
sum[0] = sum[0] + Newsrc.at<uchar>(i + r, j + c) * window.at<double>(r + hh, c + hw);
}
else if (src.channels() == 3) {
Vec3b rgb = Newsrc.at<Vec3b>(i + r, j + c);
sum[0] = sum[0] + rgb[0] * window.at<double>(r + hh, c + hw);//B
sum[1] = sum[1] + rgb[1] * window.at<double>(r + hh, c + hw);//G
sum[2] = sum[2] + rgb[2] * window.at<double>(r + hh, c + hw);//R
}
}
}
for (int k = 0; k < src.channels(); ++k) {
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (src.channels() == 1)
{
dst.at<uchar>(i - hh, j - hw) = static_cast<uchar>(sum[0]);
}
else if (src.channels() == 3)
{
Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<Vec3b>(i - hh, j - hw) = rgb;
}
}
}
}
//DOG高斯差分
void DOG1(Mat &src, Mat &dst, Size wsize, double sigma, double k = 1.6) {
Mat Mask1, Mask2, gaussian_dst1, gaussian_dst2;
generateGaussMask(Mask1, wsize, k*sigma);//获取二维高斯滤波模板1
generateGaussMask(Mask2, wsize, sigma);//获取二维高斯滤波模板2
//高斯滤波
GaussianFilter(src, gaussian_dst1, Mask1);
GaussianFilter(src, gaussian_dst2, Mask2);
dst = gaussian_dst1 - gaussian_dst2 - 1;
threshold(dst, dst, 0, 255, THRESH_BINARY);
}
//DOG高斯差分--使用opencv的GaussianBlur
void DOG2(Mat &src, Mat &dst, Size wsize, double sigma, double k = 1.6) {
Mat gaussian_dst1, gaussian_dst2;
//高斯滤波
GaussianBlur(src, gaussian_dst1, wsize, k*sigma);
GaussianBlur(src, gaussian_dst2, wsize, sigma);
dst = gaussian_dst1 - gaussian_dst2;
threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
}
// 实现
void quick_opencv::DOG_Demo(Mat &img)
{
if (img.channels() > 1) cv::cvtColor(img, img, COLOR_BGR2GRAY);
Mat edge1, edge2;
DOG1(img, edge1, cv::Size(7, 7), 2);
DOG2(img, edge2, cv::Size(7, 7), 2);
namedWindow("My_DOG", WINDOW_NORMAL);
imshow("My_DOG", edge1);
namedWindow("Opencv_DOG", WINDOW_NORMAL);
imshow("Opencv_DOG", edge2);
}