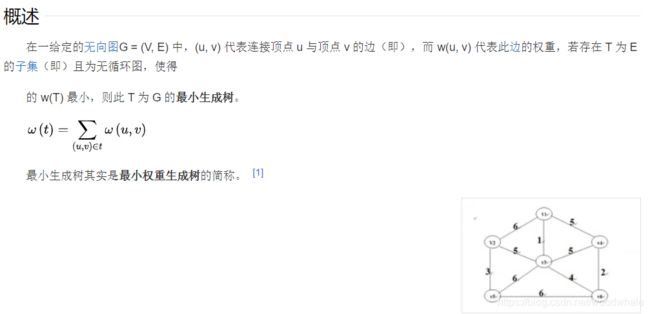
【数据结构与算法】最小生成树与最短路径问题

求最小生成树的算法和求最短路径的算法

最小生成树的概述：

最短路径的概述：

最小生成树算法

kruskal算法

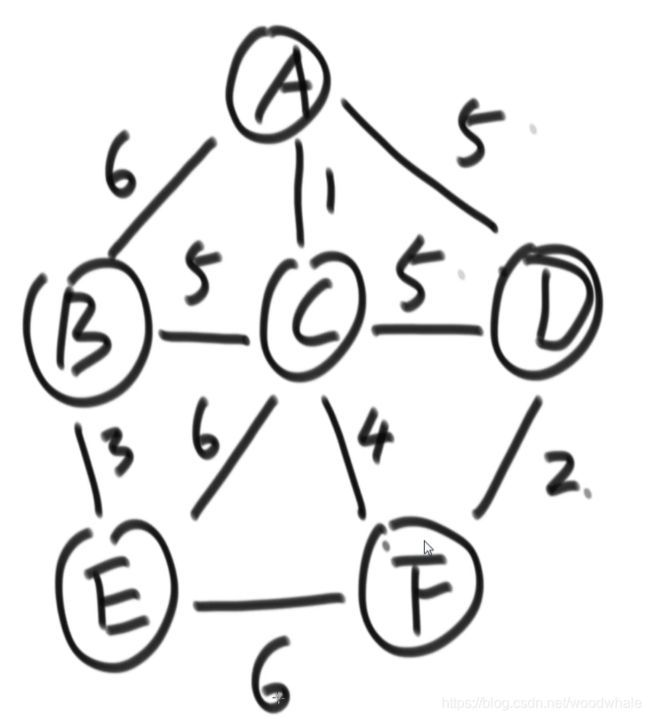
算法核心思想：

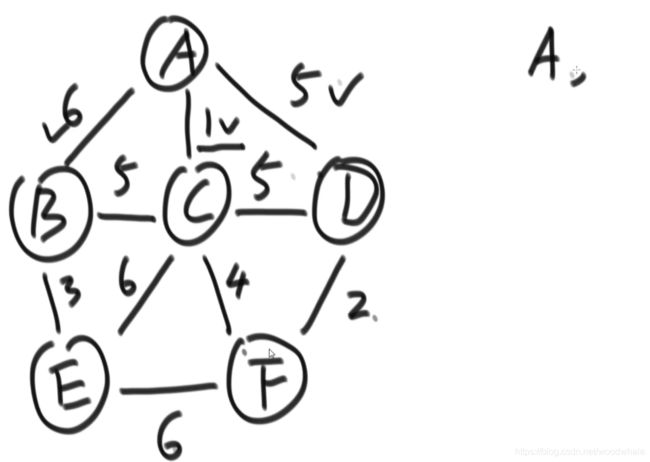
从最小边考虑，
把这条最小边加上，判断是否形成环。
如果加上没环，就加上这条最小边。
如果加上有环，跳过这条最小边。

问题：考察如何判断 《加边是否成环》这个问题！

答：使用并查集结构！

假设，每个节点自己是一个集合。
遍历节点时，判断这条边的两个节点（form、to）是否在一个节点里，不在就说明不成环。将这两个节点的集合，合二为一。选择该边。
如果这两个节点在同一个集合里，放弃该边。

由于知识水平受限，每学过并查集结构，写一个简单版本！

部分代码为伪代码！看懂思路即可！

public static class MySets{
    
    public HashMap<Node, List<Node>> setMap;
    
    public MySets(List<Node> nodes) {
        for (Node cur : nodes) {
            List<Node> set = new ArrayList<Node>();
            set.add(cur);
            setMap.put(cur, set);
        }
    }
    
    public boolean isSameSet(Node from, Node to) {
        List<Node> fromSet = setMap.get(from);
        List<Node> toSet = setMap.get(to);
        // 判断toSet和fromSet的地址是否相同
        return fromSet == toSet;
    }
    
    public void union(Node from, Node to) {
        List<Node> fromSet = setMap.get(from);
        List<Node> toSet = setMap.get(to);
        // 把to中所有的node都加到form中去，将to中所有的node指向fromSet
        for (Node toNode : toSet) {
            fromSet.add(toNode);
            setMap.put(toNode, fromSet);
        }
    }
}


public static Set<Edge> kruskalMST(Graph graph) {
    // graph.nodes.values()方法返回的是装有图中所有节点的List集合
    Mysets mysets = new Mysets(graph.nodes.values());
    // EdgeComparator()比较的是优先小边
    PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
    for (Edge edge : graph.edges) {
        priorityQueue.add(edge);
    }
    Set<Edge> result = new HashSet<>();
    while (!priorityQueue.isEmpty()) {
        Edge edge = priorityQueue.poll();
        if (!mysets.isSameSet(edge.from, edge.to)) {
            result.add(edge);
            mysets.union(edge.from, edge.to);
        }
    }
    return result;
}

prime算法

核心思想：

从点出发
初始时每一条边都没被解锁（打勾为解锁）
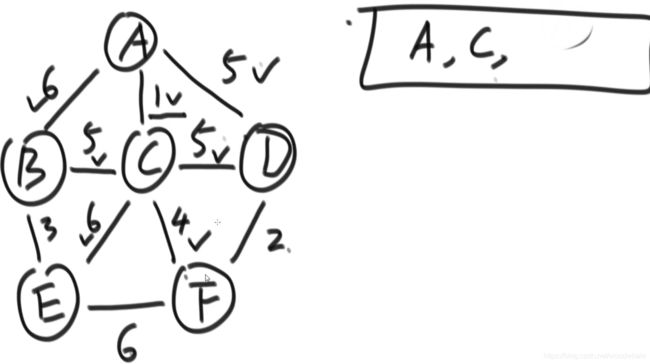
从一个节点出发，将这个节点放入set中，这个节点的边都被解锁，找这些边最小的那一条，标记这条边被使用过，这条边连接的节点加入set，其包含的边被解锁。
选择“已经解锁且没被使用过的边”中的最小的那条，标记这条边被使用过，这条边连接的节点加入set，其包含的边被解锁。
如果发现选择边时，有多条权值相同的边，那么不选连接到list集合中存在的节点的那些边。
重复上述过程，直到set中将图中所有节点都包含了，结束！
此时，被我们标记选择过的边都是最小边。

算法实现：用一个哈希表即可

public static Set<Edge> primMst(Graph graph) {
   
    // 解锁的边进入小根堆
    PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator);
    
    // 存放节点的set
    HashSet<Node> set = new HashSet<>();
    
    // 依次挑选的边在result中
    Set<Edge> result = new HashSet<>();
    
    // 这个foreach循环是考虑森林的问题，即不连通的多张图，都要把每张图的最小生成树加入result中，如果是一个图不需要这个foreach
    for (Node node : graph.nodes.values()) {
        
        // 随便挑一个点
        // node是开始点
        if (!set.contains(node)) {
            set.add(node);
            for (Edge edge : node.edges) {
                // 由一个点，解锁所有相连的边
                priorityQueue.add(edge);
            }
            while (!priorityQueue.isEmpty()) {
                // 弹出已经解锁的边中，最小的边
                Edge edge = priorityQueue.poll();
                // 可能的一个新的点
                Node toNode = edge.to;
                // 如果set中不含有这个toNode节点，那么用这个点
                if (!set.contains(toNode)) {
                    set.add(toNode);
                    result.add(edge);
                    for (Edge nextEdge : toNode.edges) {
                        priorityQueue.add(nextEdge);
                    }
                }
            }
        }
        
        
    }
    return result;
}

细节

k算法由于将权值排列后放入小根堆中，每次弹出的边不具有连续性，所以会存在节点跳跃的情况。

p算法由于是从点出发，每次都是选择一个点加入set，所以不会存在上述情况。但是由于我们也用了小根堆，每次加入set的新节点要重复《将这个节点的所有边加入小根堆》，会导致上次选择过的边再次加入小根堆。即使每次小根堆弹出后会判断连接的节点是否是新的，不会印象最终结果，但也会消耗更多时间。

最短路径算法

Dijkstra算法

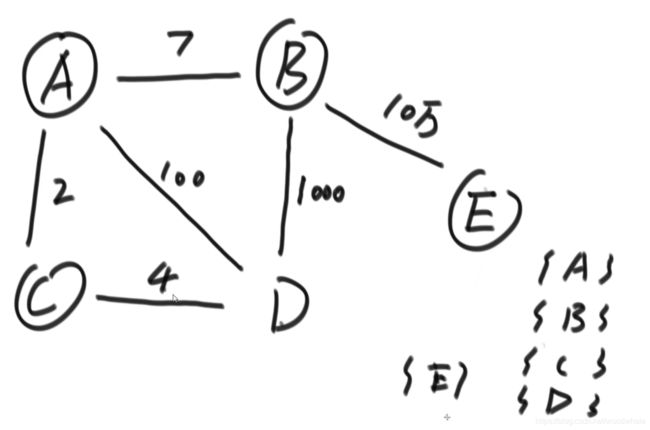
适用范围：没有权值为负数的边

一定要规定出发点

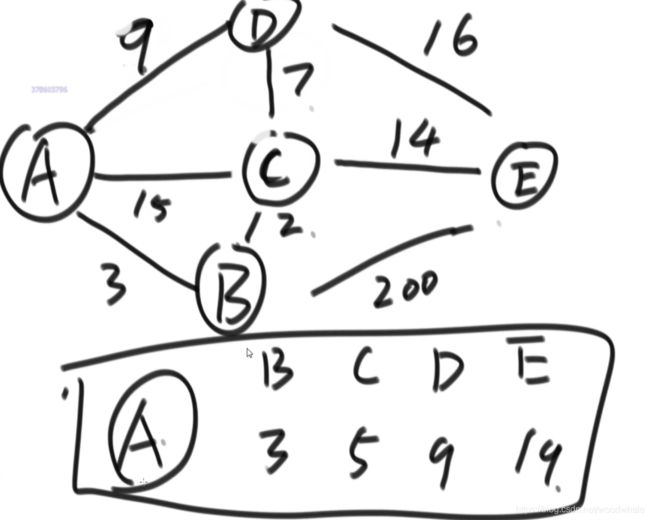
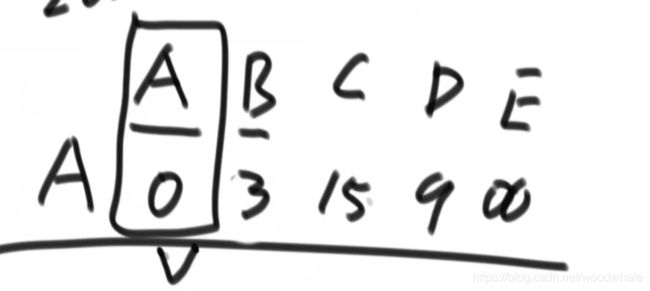
最终要的效果就是如图：

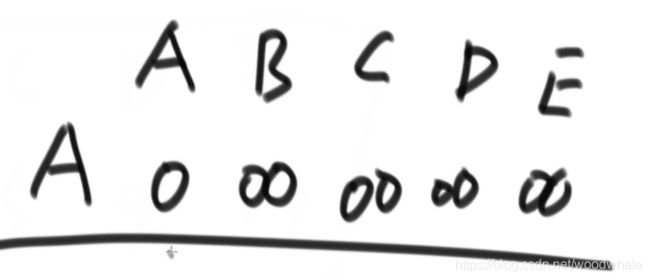
初始时：（正无穷就是哈希表没被更新过）

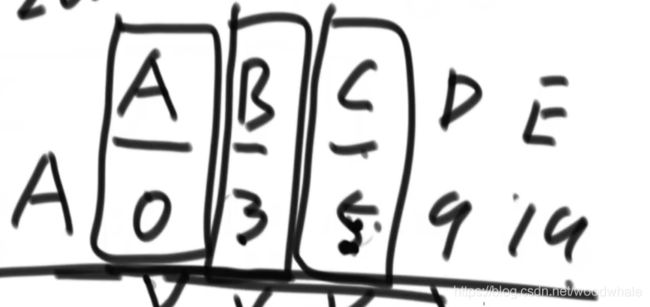
发现更短距离就更新

使用完一个一个点之后，锁死这个点

《锁死A》

最终效果：

代码实现：（伪代码）

public static HashMap<Node, Integer> dijkstra1(Node head) {
    // 从head出发到所有点的最小距离
    // key : 从head出发到达key
    // value : 从head出发到达key的最小距离
    // 如果在表中没有T的记录,含义是从head出发到T这个点的距离时无穷远
    HashMap<Node, Integer> distanceMap = new HashMap<>();
    distanceMap.put(head,0);
    // 已经求过的距离的节点,存在selectedNodes中,以后再也不碰
    HashSet<Node> selectedNodes = new HashSet<>();
    // 将头节点的连接都记录下来
    Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
    while (minNode != null) {
        int distance = distanceMap.get(minNode);
        for (Edge egde : minNode.edges) {
            Node toNode = edge.to;
            if (!distanceMap.containsKey(toNode)) {
                distanceMap.put(toNode, distance + edge.weigth);
            }else {
                distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
            }
        }
        selectedNodes.add(minNode);
        minNode =getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
    }
    return distanceMap;
}

public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> touchedNodes) {
    Node minNode = null;
    int minDistance = Integer.MAX_VALUE;
    for (Entry<Node, Integer> entry : distanceMap.entrySet()) {
        Node node = entry.getKey();
        if (!touchedNodes.contains(node) && distance < minDistance) {
            minNode = node;
            minDistance = distance;
        }
    }
    return minNode;
}

后话

这篇博客的内容是记录自己学的有关图的部分重要算法。如果喜欢《数据结构与算法》这个系列，我会长期更新！

如果你喜欢这篇文章，麻烦点个免费的赞！

如果有任何问题或者错误，欢迎在评论区指出！