LeetCode刷题day56

---

377. 组合总和 Ⅳ

题目描述

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3
输出：0

思路分析

本题描述说是求组合,但实际上是求排列!

如果本题要把所有的排列都列出来,只能使用回溯算法暴搜. 本题是求组合个数,那么通过动态规划便可以进行解决!

下面我们开始分析**动规五部曲**

1. 确定dp数组以及下标的含义

dp[i]:凑成目标整数为i的排列个数为dp[i]

2. 确定递推公式

dp[i] += dp[i - nums[j]]; dp[i]由 使用当前元素的排列个数 + 不使用当前元素的排列个数组成.

3. dp数组如何初始化

dp[0] = 1 : 凑成0的排列个数为0个,那就是向其背包加入任何数.

对于非0下标初始化为0，这样才不会影响dp[i]累加所有的dp[i - nums[j]]。

4. 确定遍历顺序

个数可以不限使用,说明这是一个完全背包! = => 背包循环正序遍历

得到的集合是排列,说明需要考虑元素之间的顺序. = => 外 层for遍历背包,内层for遍历物品.

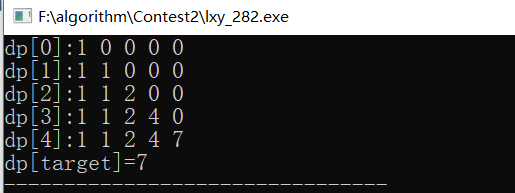
5. 举例来推导dp数组

**备注:**C++测试用例有超过两个树相加超过int的数据，所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。

参考代码

#include
using namespace std;
void print(vector<int>& dp){
	for(int i  = 0; i < dp.size(); i++){
		cout<<dp[i]<<" ";
	}
	cout<<endl;
}
//完全背包  排列(有顺序)  dp[0] =  1
int combinationSum4(vector<int>& nums, int target) {
	vector<int> dp(target+1,0);
	dp[0] = 1;
	//cout<<"dp["<<0<<"]:";
	//print(dp);
	//完全背包 排列=>外层背包,内层物品  
	for(int i = 1;i <= target; i++){//遍历背包 
		for(int j = 0;j < nums.size(); j++){//遍历物品 
			if(i-nums[j] >= 0 && dp[i] < INT_MAX - dp[i-nums[j]]){//控制dp下标范围 
				dp[i]  = dp[i]  + dp[i-nums[j]];
			}
		}
		//cout<<"dp["<
		//print(dp);
	}
	return dp[target];
}

int main(){
	vector<int> nums  = {1,2,3};
	int target = 4;
	cout<<"dp[target]="<<combinationSum4(nums,target);
	return 0;
}

70.爬楼梯

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

原题我们之前已经做过,我们现在对题目进行修改:

改为：一步一个台阶，两个台阶，三个台阶，…，直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢？ (m<=n)

思路分析

1. 确定dp数组以及下标的含义

dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法

2. 确定递推公式

dp[i]有几种来源,dp[i-1],dp[i-2],dp[i-3] …即:dp[i-j]

递推公式为:dp[i] += dp[i-j] dp[i]等于 本次将物体(步数)放入背包+本次不放入背包的情况数之和

3. dp数组如何进行初始化

dp[1] = 1 dp[2] = 2. 由于dp[i]都是由之前的累加上来的,所以dp[0] = 1.

4. 确定遍历顺序

本题属于背包求排列问题,即1、2 步 和 2、1 步都是上三个台阶，但是这两种方法不一样！

所以将背包target放在外循环,nums放在内循环.

每一步可以走多次,这是完全背包,内循环需要从前往后遍历.

5. 举例来推导dp数组,这个题和上一个基本一样…

参考代码

#include
using namespace std;

int climbStairs(int n,int m) {//n:楼梯高度  m:每次可以走1,2,...n步  暗含:n>=m哦 
	vector<int> dp(n+1,0);
	dp[0] = 1;//必须初始化为1,因为dp[0]是基础 
//	dp[1] = 1;
//	dp[2] = 2;
	//完全背包  排列 => 外层遍历背包,内层 遍历物品(每次走的台阶) 
	for(int i = 1; i <= n;i++) {//遍历背包 
		for(int j = 1; j <= m; j++){//遍历台阶  i - j >= 0
			if(i-j>=0){// 控制dp中下标的范围 
				dp[i]  = dp[i] + dp[i-j];//状态转移方程 
			}
		}
	}
	return dp[n] ;
}

322. 零钱兑换

题目描述

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

思路分析

动规五部曲

1. 确定dp数组以及下标的含义

dp[j]: 凑足总额为j所需钱币的最少个数为dp[j]

2. 确定递推公式

dp[j]有两个来源,一个是dp[j-coins[i]]:使用当前的钱币(将当前物品放入背包),另外一个是不适用当前钱币(当前物品不放入背包)

递推公式: dp[j] = min(dp[j-coins[i]] + 1,dp[j])

3. dp数组如何进行初始化

凑足总金额为0所需钱币的个数一定为0,则 dp[0] = 0

4. 确定遍历顺序

本题求的是钱币最小个数,那么钱币有没有顺序都是可以的,都不影响钱币的最小个数. 即本题不强调是组合和排列

我采用物品放在外循环,背包放在内循环.

因为钱币可以无限使用,那么就是完全背包,遍历的内循环是正序.

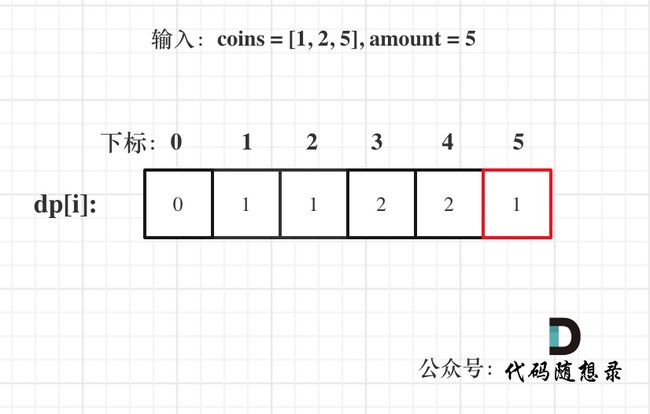
5. 举例推导dp数组

以输入：coins = [1, 2, 5], amount = 5为例

参考代码

#include
using namespace std;

int coinChange(vector<int>& coins, int amount) {
	vector<int> dp(amount+1,INT_MAX);//因为存放的是组成总金额最少硬币个数,所以初始化为最大值.
	dp[0] = 0;//初始化 凑成0 需要的硬币个数为0 
	//完全背包 
	for(int i = 0;i < coins.size();i++) {//外层遍历物品 
		for(int j = coins[i]; j <= amount; j++){//内层遍历背包 
			if(dp[j-coins[i]] != INT_MAX) {//只有能凑成j-coins[i],才可把当前物品放入.如果凑不成只能和上次一样dp[j] 
				dp[j]  = min(dp[j],dp[j-coins[i]]+1);//状态转移方程 
			}
		} 
	}
	if(dp[amount]==INT_MAX) {//如果不能够凑成当前面额 
		return -1;
	}
	return dp[amount] ;
}

279. 完全平方数

题目描述

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

思路分析

可能刚看这种题感觉没啥思路，又平方和的，又最小数的。

我来把题目翻译一下：完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，问凑满这个背包最少有多少物品？

感受出来了没，这么浓厚的完全背包氛围

动规五部曲

1. 确定dp数组以及下标的含义

dp[j]: 和为j的完全平方数的最小数量为dp[j]

2. 确定递推公式

dp[j]可以由dp[j-i*i]推出,并且我们要选择最小的dp[j].所以递推公式为dp[j] = min(dp[j- i * i]+1,dp[j])

3. dp数组如何初始化

dp[0]表示和为0的完全平方数的最小数量,那么dp[0] = 0

另外,从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，所以非0下标的dp[j]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖。

4. 确定遍历顺序

我们知道这是个完全背包.另外因为本题求的是最小数量.所以不区分排列还是组合!

本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！

5. 举例推导dp数组

已输入n为5例，dp状态图如下：

参考代码

#include
using namespace std;
//方法一:外层遍历背包 
int numSquares(int n) {
	vector<int> dp(n+1,INT_MAX) ;
	dp[0] = 0;//初始化:凑成0,需要的完全平方个数为0
	for(int i = 1; i <= n;i++) {
		for(int j = 1; j*j <= i; j++){// 完全平方数(物体)必须小于背包容量 
			dp[i] = min(dp[i],dp[i-j*j] + 1);//状态转移方程 
		}
	}
	return dp[n] ;
}

//方法二 :外层遍历物品 
int numSquares(int n) {
	vector<int> dp(n+1,INT_MAX) ;
	dp[0] = 0;//初始化:凑成0,需要的完全平方个数为0
	for(int i = 1; i*i <= n;i++){//外层遍历物品 
		for(int j = 1; j<=n;j++){//内层遍历背包 
			if(j-i*i >= 0){//对dp[x]中的x(背包剩余容量)进行限定 
				dp[j] = min(dp[j],dp[j-i*i]+1);
			}
		}
	}
	return dp[n];
}

---

如果有收获！！！ 希望老铁们来个三连，点赞、收藏、转发。
创作不易，别忘点个赞，可以让更多的人看到这篇文章，顺便鼓励我写出更好的博客