使用Open_CV对图像的简单处理

对图像的理解

1、图像可以理解为由许多像素点构成的，这些像素点是二维离散的。若横向一行有M个像素点，纵向一列有N个像素点，可以理解为一个M*N的矩阵。每个像素都有自己的位置和值。根据每个像素点包含的信息不同，图像又分为：

• 黑白图像：每个像素只能是黑或白即灰度等级只有两种0和1，没有中间过渡。
• 彩色图像：即每个像素信息由RGB构成的图像，RGB又分别由不同的灰度级描述。
• 灰度图像：即每个每个像素只有一个采样颜色的图像，显示为从最暗黑色到最亮的白色的灰度。灰度图像与黑白图像不同，在计算机图像领域中黑白图像只有黑白两种颜色，灰度图像在黑色与白色之间还有许多级的颜色深度。

2、还可以认为图像是各种波的叠加。图像中的像素点包含有不同的颜色信息，每种颜色对应不同的灰度等级，可以理解为这些值构成一条有波动的曲线，则图像又各种不同的波叠加而成。曲线波动大的地方就是图像变化的地方。这样我们可以区分图像哪些区域变化特别强，哪些区域变化不那么强。

图像的取样和量化

• 取样：采样的实质就是要用多少点来描述一幅图像。采样间隔越大，所得图像像素数越少，空间分辨率低，质量差；采样间隔越小，所得图像像素数越多，空间分辨率高，图像质量好。
• 量化：量化是指要使用多大范围的数值来表示图像取样之后的每一个点。量化的结果是图像能够容纳的颜色总数，它反映了取样的质量。

图像滤波

1、首先，百度了一下图像滤波是什么。图像滤波，即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可缺少的操作。所以可以理解为，图像滤波是对图像的操作，去除图像中的噪点而不损会坏图像的边缘。
2、理解图像求导。首先已经知道图像是一个二维的离散数集，通过推广二维连续型求函数偏导的方法，可以求得图像的偏导，也就是在（x,y）的最大变化率。
3、理解中心差分。设函数y=F(X)在等距节点Xk=X0+kh上的值F(Xk)为已知，h 是常数。
记$\Delta$Fk=Fk+1-Fk称为向前差分，$\Delta$被称作向前差分算子；
$\delta$Fk=F(k+1/2)-F(k-1/2)称为中心差分,$\delta$称为中心差分算子。
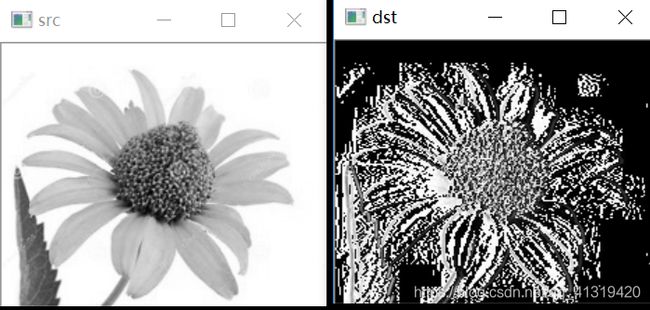
4、代码部分:此段代码对x方向进行一阶差分,对原图差分，并将值保存到dImg中,可以看出来在图像变化时的边缘情况。

#include
#define pi 3.1415926

using namespace std;
using namespace cv;

int main(int argc, char**argv)
{

	Mat src = imread("D:\\my_photos\\IMG_3143.JPG", 1);//1表示的是读取图片类型，这里读取的是彩色图象，0指读取的是灰度图象
	cvtColor(src, src, COLOR_BGR2GRAY);//将彩色图象转变为灰度图像
	namedWindow("src", WINDOW_AUTOSIZE);//新建一个窗口
	imshow("src", src);//在打开的窗口展示图片 
	//差分
	Mat dImg = Mat(src.rows, src.cols - 2, CV_8UC1);//1表示通道数，因为转为灰度图像R=G=B,所以取一个通道
	for (int i = 0; i < src.rows; i++)//行
	{
		for (int j = 1; j < src.cols - 1; j++)//列
		{
			dImg.at<uchar>(i, j - 1) = src.at<uchar>(i, j + 1) - src.at<uchar>(i, j - 1);//放到中间位置，后边两个遍历原图
		}
	}
	cvNamedWindow("dst", CV_WINDOW_AUTOSIZE);//新建一个窗口
	imshow("dst", dImg);//用于图片展示，第一个参数为窗口名称，第二个为图片内容
	waitKey(0);//暂停
}

高斯滤波

1、高斯滤波应用于图像处理的减噪过程，高斯滤波的具体操作是：用一个卷积模板扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。可以理解为对图像进行加权平均的过程，得到的每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到的。
2、二维高斯函数为：G（x,y）=exp^(-x^2-y^2)/(2*$\sigma$^2)/2*$\sigma$^2*$\pi$
3、卷积核：百度一下可以看到它的作用为：“通过它来将图像数据进行能量转化，能量低的就排除掉，噪声属于低能量部分。”在编程中会应用在原图像的一个区域，并由此生成目标图像的一个像素，中间一个像素点就等于它周围像素值的均值，达到平滑的目的。通过卷积核在原图像上的移动就可以对图像进行处理计算。
4、卷积核的运算：通过二维高斯函数计算。x^2和y^2的平方分别表示的是邻域内其他像素与邻域内中心像素的距离，$\sigma$代表的是标准差。$\sigma$越小，二维高斯图像越窄小，平滑效果不明显；$\sigma$越大，而为高斯图像越矮宽，滤波效果比较明显。
5、归一化 百度发现归一化的原因是这样：在实际应用中，在计算离散近似的时候，在大概3σ距离之外的像素都可以看作不起作用，这些像素的计算也就可以忽略。可以理解为为了尽可能的模拟高斯函数的性质，减小误差，计算高斯模板的时候各个数值其和必须为1，所以要归一化。
6、代码如下：

#include
#define pi 3.1415926

using namespace std;
using namespace cv;

int main(int argc, char**argv)
{
	Mat src = imread("D:\\my_photos\\IMG_3143.JPG", 1);//读原图，第一个参数为图片名，第二个参数为读取类型1为彩色图像，0为灰度图像；将图片内容放到返回值中
	cvtColor(src, src, COLOR_BGR2GRAY);//将彩色图像转为灰度图像
	namedWindow("src", WINDOW_AUTOSIZE);//新建一个窗口
	imshow("src", src);//在打开的窗口展示图片,用灰度值；第一个参数为窗口名，第二个为图片内容，为int或char
	//5*5卷积核模板
	Mat model = Mat(5, 5, CV_64FC1);//double类型
	//建立卷积核模板
	double sigma = 80;
	for (int i = -2; i <= 2; i++)
	{
		for (int j = -2; j <= 2; j++)
		{
			model.at<double>(i + 2, j + 2) = exp(-(i*i + j * j) / 2 * sigma*sigma)/(2*pi*sigma*sigma);//利用二维高斯公式计算卷积核
		}
	}
	double gaussSum = 0;
	gaussSum = sum(model).val[0];//卷积核的和
	//归1化
	for (int i = 0; i < model.rows; i++)
	{
		for (int j = 0; j < 5; j++)
		{
			model.at<double>(i, j) = model.at<double>(i, j) / gaussSum;//对卷积核中的每个元素除以卷积核的核
		}
	}
	//高斯滤波后的图像，因为为5*5的模板，所以左右各有两列上下各有两行不能运算得到中间像素的均值
	Mat dst = Mat(src.rows - 4, src.cols - 4, CV_8UC1);
	//卷积核扫描原图像
	for (int i = 2; i < src.rows - 2; i++)
	{
		for (int j = 2; j < src.cols - 2; j++)
		{
			double sum = 0;
			for (int m = 0; m < model.rows; m++)
			{
				for (int n = 0; n < model.cols; n++)
				{
					sum += (double)src.at<uchar>(i + m - 2, j + n - 2)*model.at<double>(m,n);
				}
			}
			dst.at<uchar>(i - 2, j - 2) = (uchar)sum;
		}
	}
	namedWindow("gaussBlur", WINDOW_AUTOSIZE);
	imshow("gaussBlur", dst);
	waitKey(0);
}